Guide de calcul pour la conception d'une semelle isolée selon la norme CSA A23.3-14

La Fondation SkyCiv couvre la conception de semelles isolées conformes à la CSA A23.3-14¹ et au NBCC 2010².

Vous voulez essayer le logiciel Foundation Design de SkyCiv? Notre outil permet aux utilisateurs d'effectuer des calculs Foundation Design sans aucun téléchargement ni installation!

Calculatrice de conception de fondation

Paramètres de conception d'une semelle isolée

Certains calculs présentés sont similaires avec ACI 318, qui est aussi une des références de son homologue CSA.

Exigences de dimension

Pour déterminer les dimensions d'une semelle isolée, service ou charges non pondérées, comme mort (D), Habitent (L), Vent (W), Sismique (E), etc sera appliqué en utilisant des combinaisons de charges, tel que défini par le NBCC 2010. La combinaison de charges qui régit sera considérée comme la charge de conception, et sera divisé par la pression admissible du sol, comme indiqué dans l'équation 1.

\(\texte{A} = frac{\texte{P}_{\texte{n}}}{\texte{q}_{\texte{tout}}} \flèche droite \) Équation 1

où:
q_tout = pression du sol admissible
P_n = charge de conception non pondérée
A = zone de fondation

Cisaillement unidirectionnel

Pour vérifier cisaillement unidirectionnel, le plan de cisaillement critique (Reportez-vous à la figure 1) est situé à distance “d” de la face d'une colonne.

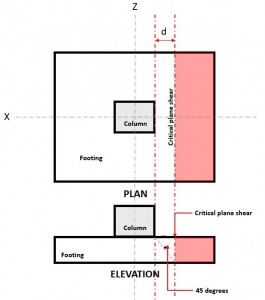
Figure 1. Cisaillement plan critique du cisaillement unidirectionnel

Le Une manière Tondre Demande ou V_F est calculé en supposant que la semelle est en porte-à-faux du poteau où se trouve la surface (rouge) indiqué sur la figure 2, conformément à CSA A23.3-14, Section 13.3.6.

Le Capacité de cisaillement unidirectionnelle ou V_c est définie comme la résistance ultime au cisaillement et calculée à l'aide de l'équation 2 par CSA A23.3-14, Section 11.3.4.

\(\texte{V}_{\texte{c}} = phi _{\texte{c}} \fois lambda fois sqrt{\texte{F'}_{\texte{c}}} \fois texte{b}_{\texte{w}} \fois texte{d} \flèche droite \) Équation 2 (CSA A23.3-14 Éq.. 11-6)

où:
ϕ_c = facteur de résistance du béton
λ = facteur de modification de la densité du béton
F’_c = résistance du béton spécifiée, MPa
b_w = largeur de la semelle, mm
d = profondeur de cisaillement effective, mm

La demande de cisaillement et la capacité de cisaillement doivent répondre à l'équation suivante pour répondre aux exigences de conception de CSA A23.3-14:

\(\texte{V}_{\texte{F}} \leq phi text{V}_{\texte{c}} \flèche droite \) Équation 3 (CSA A23.3-14 Eq. 11.3)

Fondation SkyCiv, conformément à l'équation 3, calcule le rapport d'unité de cisaillement unidirectionnel (Équation 4) en prenant la demande de cisaillement sur la capacité de cisaillement.

\( \texte{Ratio d'unité} = frac{\texte{Demande de cisaillement}}{\texte{Capacité de cisaillement}} \flèche droite \) Équation 4

Cisaillement bidirectionnel

Le Cisaillement bidirectionnel état limite, aussi connu sous le nom poinçonnage, étend la section critique à une distance “j / 2” de la face de la colonne et autour du périmètre de la colonne. Le plan de cisaillement critique est situé à cette section de la semelle (Reportez-vous à la figure 2).

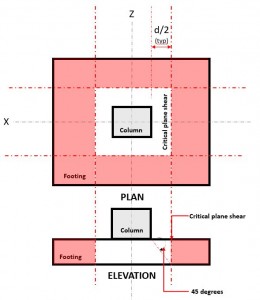
Figure 2. Plan de cisaillement critique du cisaillement bidirectionnel

Le Deux voiesentendre la demande ou V_F se produit au plan de cisaillement critique, situé à une distance de “j / 2” où le (rouge) zone hachurée, indiqué sur la figure 2, conformément à CSA A23.3-14, Section 13.3.3.

Le Capacité de cisaillement ou V_c est régi par la plus petite valeur calculée à l'aide de l'équation 5, 6, et 7 par CSA A23.3-14, Section 13.3.4.1

\(\texte{V}_{\texte{c}} = gauche ( 1 + \frac{2}{\afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués{\texte{c}}} \droite ) \fois 0.19 \fois lambda times phi _{\texte{c}} \fois sqrt{F'_{c}} \flèche droite \) Équation 5 (CSA A23.3-14 Eq. 13.5)

\(\texte{V}_{\texte{c}} = gauche ( \frac{\alpha_{\texte{s}} \fois texte{d}}{\texte{b}_{\texte{le}}} + 0.19 \droite ) \fois lambda times phi _{\texte{c}} \fois sqrt{F'_{c}} \flèche droite \) Équation 6 (CSA A23.3-14 Eq. 13.6)

\(\texte{V}_{\texte{c}} = 0.38 \fois lambda times phi _{\texte{c}} \fois sqrt{F'_{c}} \flèche droite \) Équation 7 (CSA A23.3-14 Eq. 13.7)

Remarque: b_c est le rapport entre le côté long et le côté court de la colonne, charge concentrée, ou zone de réaction et α_s est donné par 13.3.4.1

où:
λ = facteur de modification de la densité du béton
F’_c = résistance du béton à la compression spécifiée, MPa
d = distance entre la fibre de compression extrême et le centre de gravité de l'armature de tension longitudinale, mm

La demande de cisaillement et la capacité de cisaillement doivent répondre à l'équation suivante pour répondre aux exigences de conception de la CSA A23.3-14.:

\(\texte{V}_{\texte{F}} \leq phi text{V}_{\texte{c}} \flèche droite \) Équation 8 (CSA A23.3-14 Eq. 11.3)

Fondation SkyCiv, conformément à l'équation 8, calcule le rapport unitaire de cisaillement bidirectionnel (Équation 9) en prenant la demande de cisaillement sur la capacité de cisaillement.

\( \texte{Ratio d'unité} = frac{\texte{Demande de cisaillement}}{\texte{Capacité de cisaillement}} \flèche droite \) Équation 9

Flexion

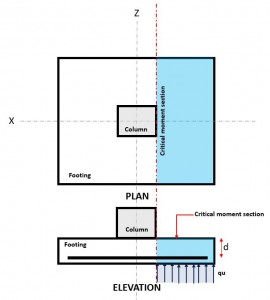
Figure 3. Section de flexion critique

Le Flexural l'état limite se produit à la section de flexion critique, situé à l'avant du poteau au-dessus de la semelle (Reportez-vous à la figure 3).

Le Demande momentanée, ou M_F est situé dans la section de flexion critique (zone de hachures bleues) indiqué sur la figure 3, et est calculé à l'aide de l'équation 10.

\( \texte{M}_{u} = texte{q}_{u} \fois gauche ( \frac{l_{X}}{2} – \frac{c_{X}}{2} \droite ) \fois l_{z} \fois gauche ( \frac{\frac{l_{X}}{2} – \frac{c_{X}}{2} }{2} \droite ) \flèche droite \) Équation 10

où:
q_u = pression du sol pondérée, kPa
l_X = cote de la semelle le long de l'axe des x, mm
l_z = cote de la semelle le long de l'axe z, mm
c_X = dimension de la colonne le long de l'axe des x, mm

Le Moment de résistance, ou Mr est calculé à l'aide de l'équation 11.

\( \texte{M}_{r} = phi_{\texte{s}} \fois A_{s} \fois f_{Y} \fois gauche( d – \frac{a}{2} \droite) \flèche droite \) Équation 11

où:
ϕ_s = facteur de résistance pour les barres d'armature non précontraintes
d = distance entre la fibre de compression extrême et le centre de gravité de l'armature de tension longitudinale, mm
A_s = zone de renforcement, mm²
a = profondeur du bloc de contrainte rectangulaire équivalent, mm
fy = force de renforcement, MPa

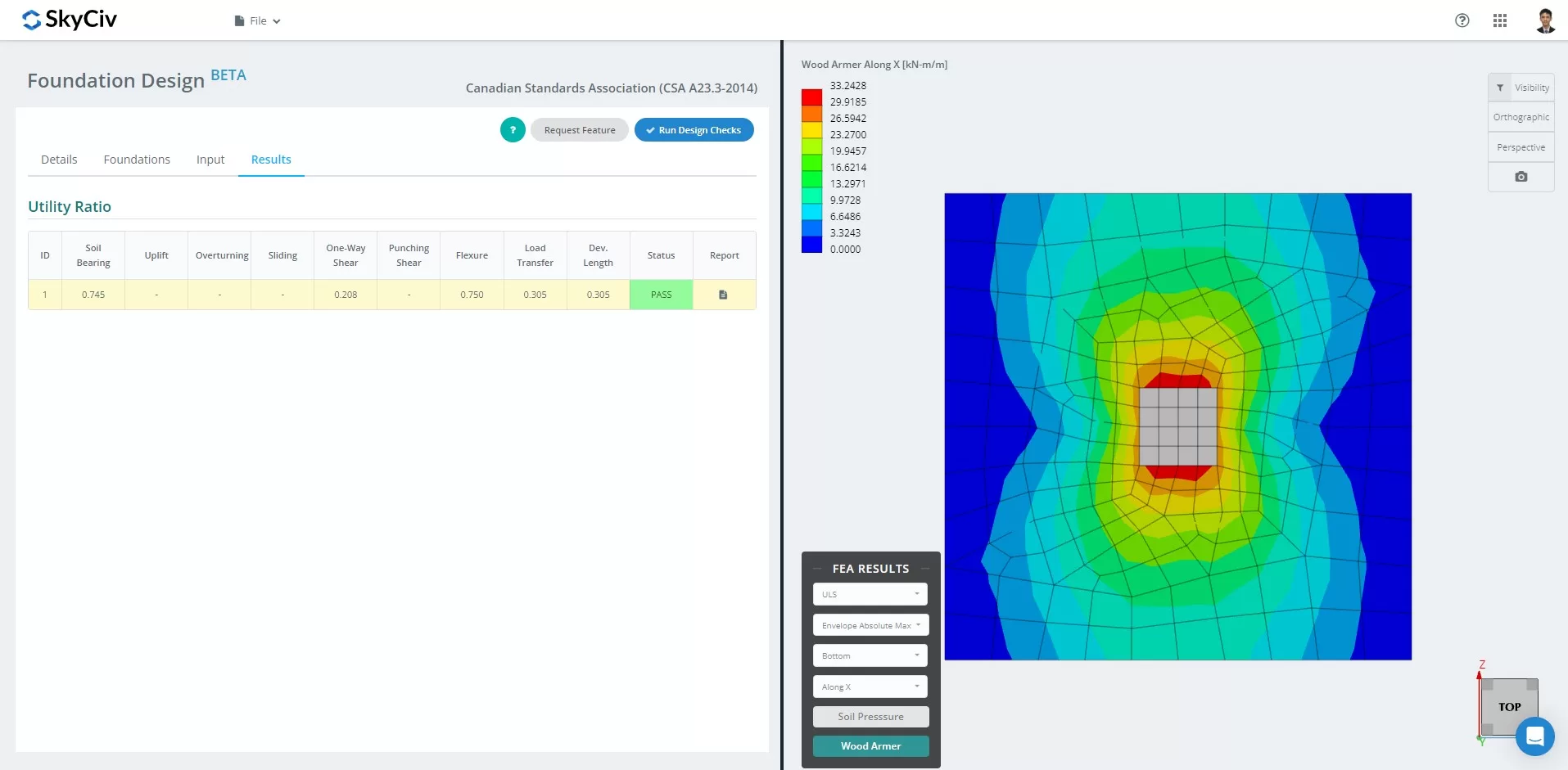
NOUVELLE Fondation SkyCiv avec FEA

Dès mars 2024, le module de conception de fondation a intégré l'analyse par éléments finis (LAID) solveur dans ses capacités. Cette nouvelle fonctionnalité permet aux utilisateurs d'effectuer des analyses approfondies de la pression du sol et de l'armement du bois tout en effectuant toutes les vérifications structurelles spécifiées par la CSA A23.3-14., incluant toutes les vérifications mentionnées ci-dessus. Le résumé des résultats de l’AEF est inclus dans le rapport complet.