讲解: 如何使用截面方法求解桁架结构
在本教程中, 我们将探索和学习使用截面法解决您的桁架结构的好处. 什么是桁架? 如果您不确定, 访问我们的 什么是桁架 文章. 截面法用于快速求解较大的桁架结构, 简单的方式. 涉及裁切’ 通过许多成员来评估其轴向力，并以此为基础来解决桁架结构的其余部分.
最棒的是, SkyCiv桁架 自动为您执行此操作. 为您自己的桁架建模，软件将显示交互式逐步解决部分方法!
观看视频教程
观看视频教程
示例问题
对于我们的工作示例, 我们将研究以下问题:
题: 使用节的方法, 确定成员的力量 10, 11, 和 13 以下桁架结构:
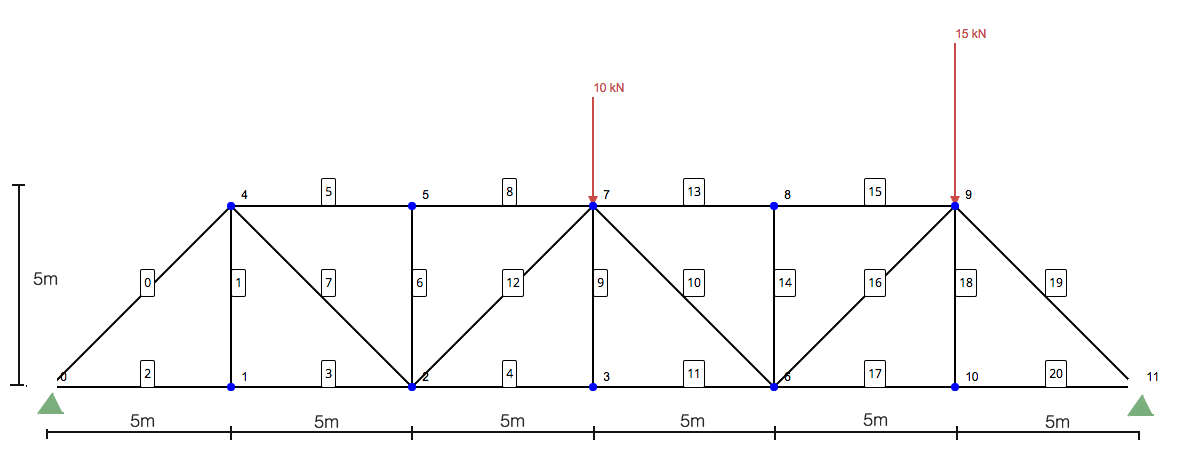
步 1: 计算对支持物的反应
像大多数静态结构分析一样, 我们必须首先找到并解决 支持者的反应. 这将为我们提供解决桁架结构所需的边界条件. 简化结构以仅包括载荷和支撑:
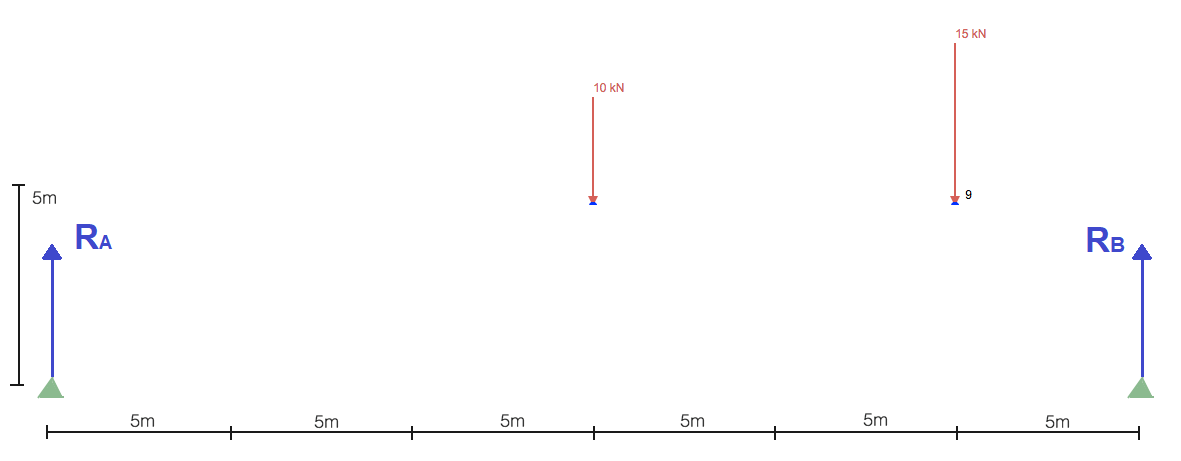
无需花费太多时间来计算反应, 通常，您需要先计算一个点的总和. 花费关于左支撑的总和可以使我们:
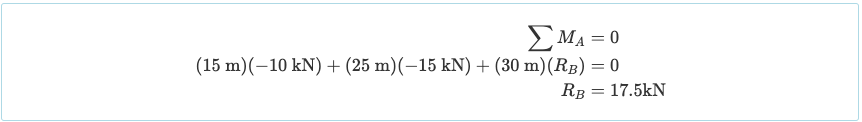
所以反应在正确的支持下 ([R乙) 是 17.5 kN向上. 现在, 取y中的力之和给我们反作用力R一个 向上为7.5kN:
步 2: 切入感兴趣的成员
这是使用截面方法解决桁架的最重要部分. 它涉及通过您要解决的成员切成薄片. 这种结构分析方法在尝试解决某些构件而不必使用接缝法解决整个结构时非常有用. 所以, 在我们的示例中，这将是我们的切片:
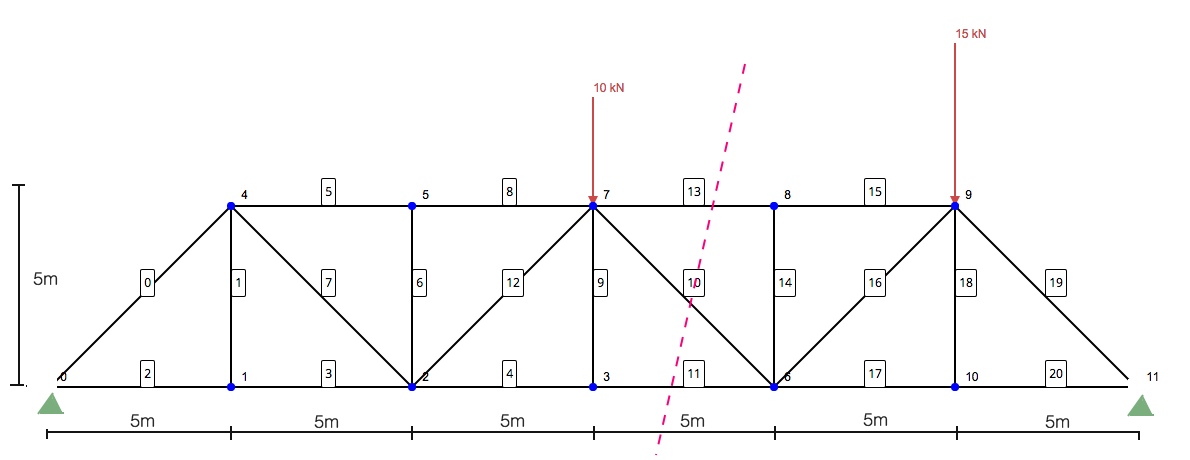
只聚焦在左侧, 您将拥有以下结构:
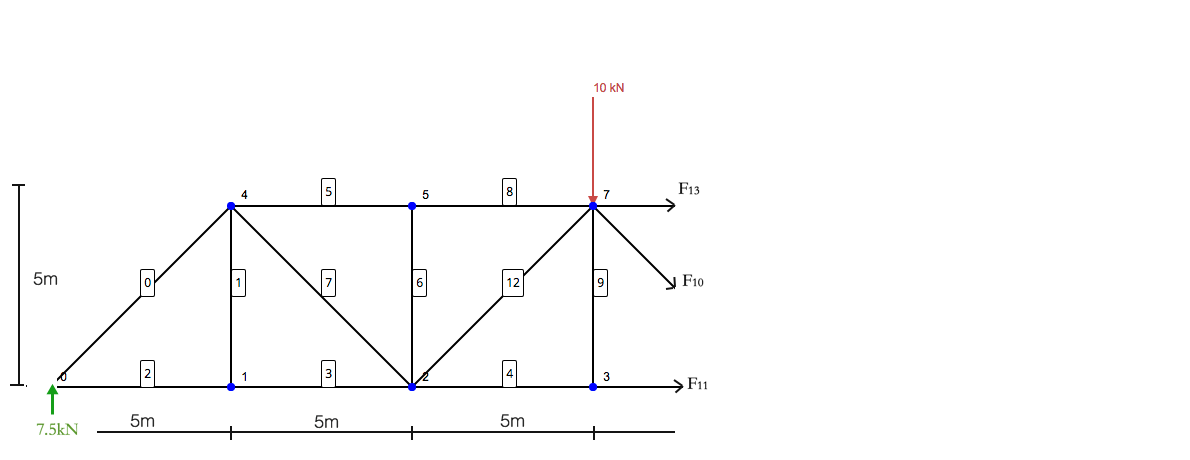
现在把这个结构想象成一个独立的结构. 静定律仍然适用 – 所以力矩和力的总和必须等于零. 带箭头的成员 (F13, F10, F11) 是什么使反应和作用在结构上的力稳定. 注意，力矩的总和是关于节点的 7 – 因为会排除成员的力量 13 和 10 – 离开F11 被隔离.
使用上面的自由身图, 我们可以得到以下公式:
y方向上的力之和:
[数学]
\开始{对齐}
+\向上箭头文本{ } \和{F_y} &= 0\\
7.5\文本{ 千牛} – 10 \文本{ 千牛} – F_{10}没有(45^{\马戏团}) &= 0\\
F_{10} &= -3.536 \文本{ 千牛}
\结束{对齐}
[数学]
关于节点的总和 7:
[数学]
\开始{对齐}
+\圆箭头左文本{ } \和{M_7} &= 0\\
-(15 \文本{ 米})(7.5 \文本{ 千牛}) + (5 \文本{ 米})F_{11} &= 0\\
F_{11} &= 22.5 \文本{ 千牛}
\结束{对齐}
[数学]
x方向上的力总和:
[数学]
\开始{对齐}
+\右箭头文本{ } \和{F_x} &= 0\\
F_{13} + F_{11} + F_{10}cos(45^{\马戏团}) &= 0\\
F_{13} &= -F_{11} – F_{10}cos(45^{\马戏团}) \\
F_{13} &= – (22.5 \文本{ 千牛}) – (-3.536 \文本{ 千牛})cos(45^{\马戏团}) \\
F_{13} &= -22.5 \文本{ 千牛} + (3.536 \文本{ 千牛})cos(45^{\马戏团}) \\
F_{13} &= -20 \文本{ 千牛}
\结束{对齐}
[数学]
最终解决方案
我们可以使用这些结果来解决桁架结构中的剩余构件. 分段法. 作为参考, 整个Truss结构的结果可以在下面找到 (使用我们的 桁架计算器) 这非常适合检查您的答案!
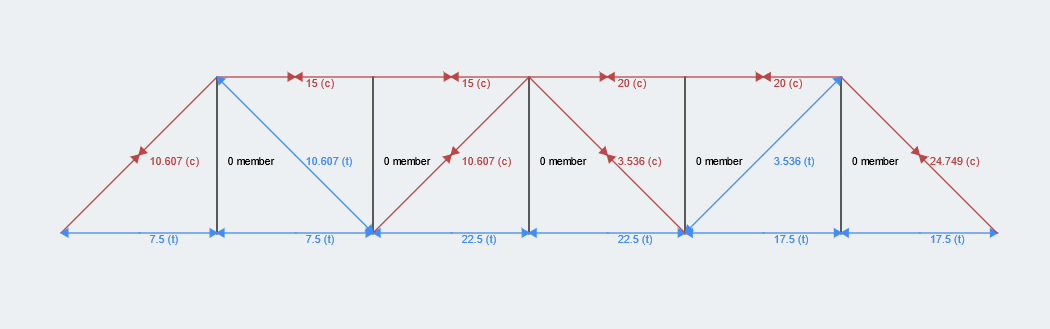
步骤总结
- 始终从计算支撑处的反应开始
- 通过您要解决的成员切成薄片
- 将半结构视为自己的静态桁架
- 通过取力之和来求解桁架= 0
- 花一点时间了解一个由多个未知成员组成的节点
SkyCiv桁架软件
我们希望您发现本教程对您的项目有用. 访问我们的 桁架教程 有关桁架的更多有用信息，别忘了查看我们的 用节点法求解桁架的指南.
SkyCiv桁架 可以自动为您计算截面的方法. 或者试试我们的 免费桁架计算器 这会给你最终的答案 (没有手工计算).
探索 SkyCiv 软件的更多功能, 今天注册开始!
