惯性矩是结构工程中使用的重要几何特性. 它与您的部分具有的材料强度直接相关. 通常, 较高的惯性矩意味着截面的强度较大, 导致承受负载时的挠度减小. 指定 “惯性矩” 实际上是一个广泛使用的用词不当, 因为这个属性与惯性无关. 正确的技术名称实际上是 面积二阶矩. 该名称更准确地描述了该属性所测量的内容, 可以粗略地视为截面面积距中性轴多远的度量.
目录
矩形公式的转动惯量
用于确定矩形转动惯量的一般公式为:
[数学] 一世_{xx}[object Window]{BD^3}{12} , 一世_{y}[object Window]{B^3D}{12} [数学]
在哪里 xx 和 y 参考特定轴, 或方向, 正在考虑.
这是一个常见的结构工程惯例 乙 指的是 宽度 矩形的, 平行于传统 水平的 x轴.
相似地, d 指的是 深度 矩形的, 平行于传统 垂直 y轴.
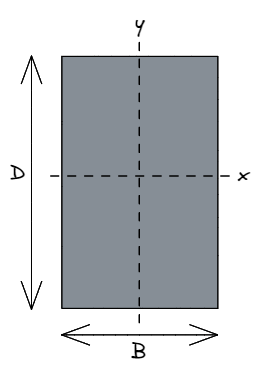
当结构工程师参考 Ixx 他们正在参考一个部分的强度 关于 x轴, 意思是平行于 d 方面, 或 y 轴. 相似地, 年年 指强度 关于 y轴, 意思是平行于 乙 方面, 或 x 轴.
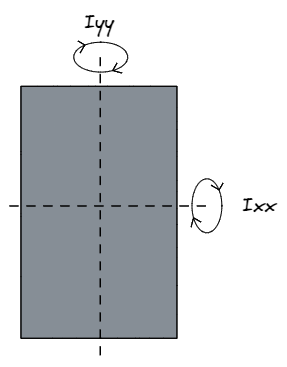
矩形空心截面 (RHS)
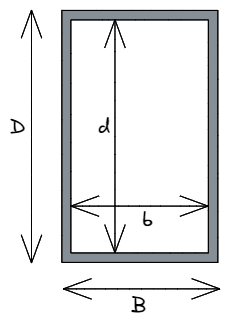
虽然工程师在设计时可以假设使用实心矩形截面, 这将使用大量的原材料, 随着重量和成本的相应增加. 使用矩形更为常见 空心型材 (通常被称为 RHS). 在这里,我们可以将上面定义的相同方程用于一般矩形情况, 然而, 我们必须减去内在 空洞的 矩形的面积:
[数学] 一世_{xx}[object Window]{BD^3}{12} – \dfrac{bd^3}{12} [数学]
在这种情况下, 小写 b 和 d 表示矩形中空心区域的大小,我们必须从形状的外部尺寸中减去, 大写 乙 和 d. 每个对应尺寸的差值是指该尺寸材料的厚度 – 即. 乙 – b = 平行于 x 轴的材料总厚度.
除了重量和材料使用的明确例子, 为什么空心部分经常被描述为更多 有效率的 比他们坚实的同行?
考虑一个向下承受垂直载荷的梁. 我们预计材料的最顶层纤维会承受压缩力, 而相应的底部纤维将承受拉力. 沿截面中性轴的纤维 (平行于截面的质心) 然而, 既不会受压也不会受拉, 由此得名 中性的 轴.
重要的, 的 震级 这些压缩力或拉伸力的大小取决于距该中性轴的距离 – 材料 更近 到中性轴需要抵抗 较少的 力.
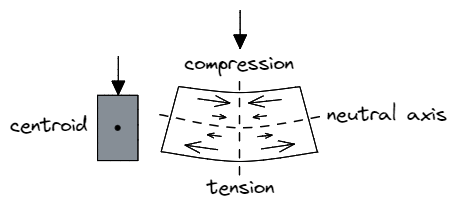
结果是, 实心部分的内部材料仅能抵抗少量的力,同时占据较大的面积, 因为最外面的材料承受最大的载荷! 移除该部分的内部并使其中空,从而改善了 效率 该部分的重量, 成本, 和材料使用.
结论
综上所述, 确定矩形转动惯量的公式为 Ixx=BD³ ⁄ 12, Iyy=B³D ⁄ 12. 对于矩形空心型材, 公式是 Ixx=BD³ ⁄ 12 – bd³ ⁄ 12.
力矩惯性对于弯矩力/应力和挠度都很重要. 这在他们的公式中很明显, 在这两种情况下, 一世 (惯性矩) 在分母中:

资源: 弯曲应力公式
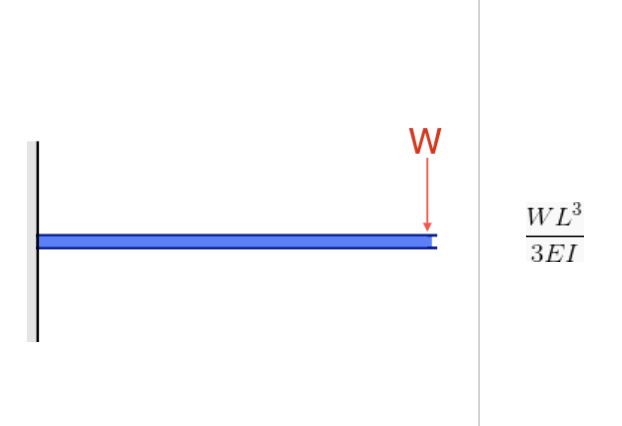
资源: 详细分解
圆的转动惯量计算器
如果你想了解更多, 查看我们的教程 圆的转动惯量 查看圆形和矩形截面形状的比较.
惯性矩免费计算器
使用我们的 惯性矩免费计算器 尝试上述计算.
为了更详细的分析, 注册以开始使用我们的完整版 SkyCiv版块生成器 版本!


