一般说明
SkyCiv 拥有强大且先进的钢筋混凝土板设计模块. 要访问此功能, 您必须先在SkyCiv S3D上建立模型,然后使用不同的构建代码(例如ACI-318)调用模块进行自动计算, 欧洲和澳大利亚标准的钢结构基础板设计, 等等. 该模块进行板设计的主要目的是提供沿板的钢筋数量.
数字 1. SkyCiv 板设计模块
如果你是 SkyCiv 的新手, 自行注册并测试软件!
SkyCiv 文档提供了精彩的内容, 包括示例和案例分析, 既可以用于学习模块(如果您是模块新手),也可以用于将板设计模块的结果与手工计算进行比较. 请随意检查我们的设计示例 ACI-318, EUROCODE, 和 AS3600.
我们建议您在深入分析复杂的板系统之前先阅读本文. 这里, 您将了解弯矩如何根据板平面尺寸而变化. 有两个案例进行研究, 单向和双向板. 所以, 让我们开始阅读!
单向与双向板行为
让我们考虑下图中的板示例, 每个板边缘都有支撑的地方, 我们确定这将充当双向板, 那是, 在两个主要平面方向上具有弯矩.
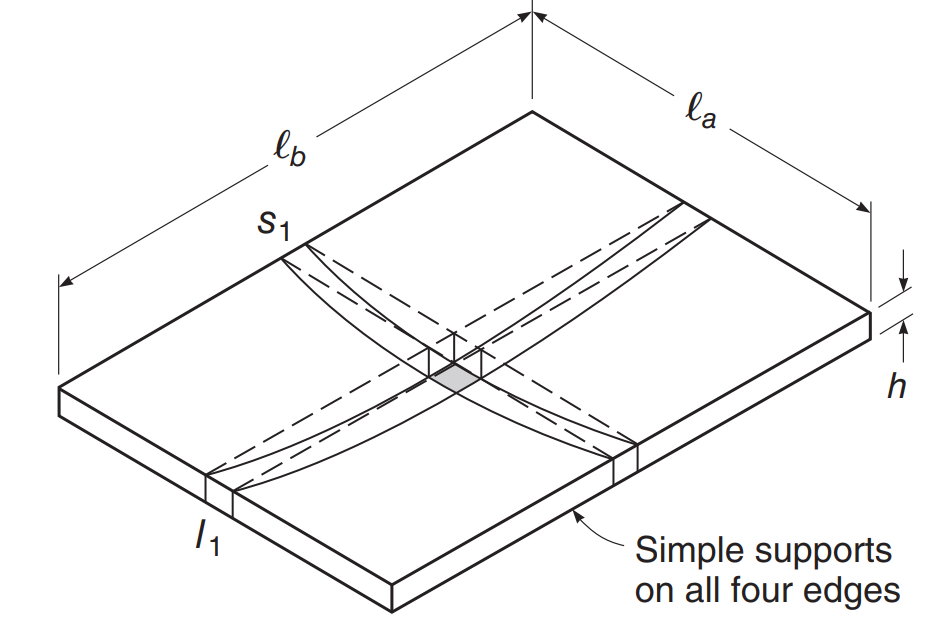
数字 2. 简单的双向板弯曲示例. (大卫·达尔文, 查尔斯·W·多兰, 亚瑟·H. 尼尔森, “混凝土结构设计,” 第十五版, 麦格劳-希尔教育)
我们可以将垂直位移定义为 (\(l_a < 磅 \)):
\(\Delta_a = \frac{{5}{w_a}{l_a^4}}{384{Ë}{一世}}\)
\(\Delta_b = \frac{{5}{w_b}{l_b^4}}{384{Ë}{一世}}\)
由于板坯是一个连续系统, 两个垂直偏转值相同. 我们可以比较方程来表达每个方向承载的载荷与平面尺寸的函数之间的关系.
\(\Delta_a = \Delta_b \to \frac{{5}{w_a}{l_a^4}}{384{Ë}{一世}} = frac{{5}{w_b}{l_b^4}}{384{Ë}{一世}}\)
\(\压裂{w_a}{w_b} = {(\压裂{磅}{l_a}})^4 \)
所有钢筋混凝土楼板设计参考均分为单向和双向,如果 \(\压裂{磅}{l_a}\) 大于或小于某个值 2, 分别.
使用上面的方程, 什么时候 \(\压裂{磅}{l_a}=2\), 短方向承载的载荷等于 \(w_a = {16}{w_b}\) 当值为 \(\压裂{磅}{l_a}=1), 载荷在两个方向上均匀分布 \(w_a ={w_b}\).
单向板时刻
所以, 我们可以看到,当维度的商大于 2, 几乎, 所有载荷和弯矩将仅集中在短方向上. 这种情况是单向平板行为, 最大弯矩可由单一宽度简支梁获得.
\(M_{最高,1,d}= 分数{{w_a}{1 米}{l_a^2}}{8}\)
双向板时刻
双向板案例的求解是结构力学中一个复杂且具有挑战性的问题. 您可以在下图中看到一般分析由一个板组成,每个方向都有全部力和力矩.
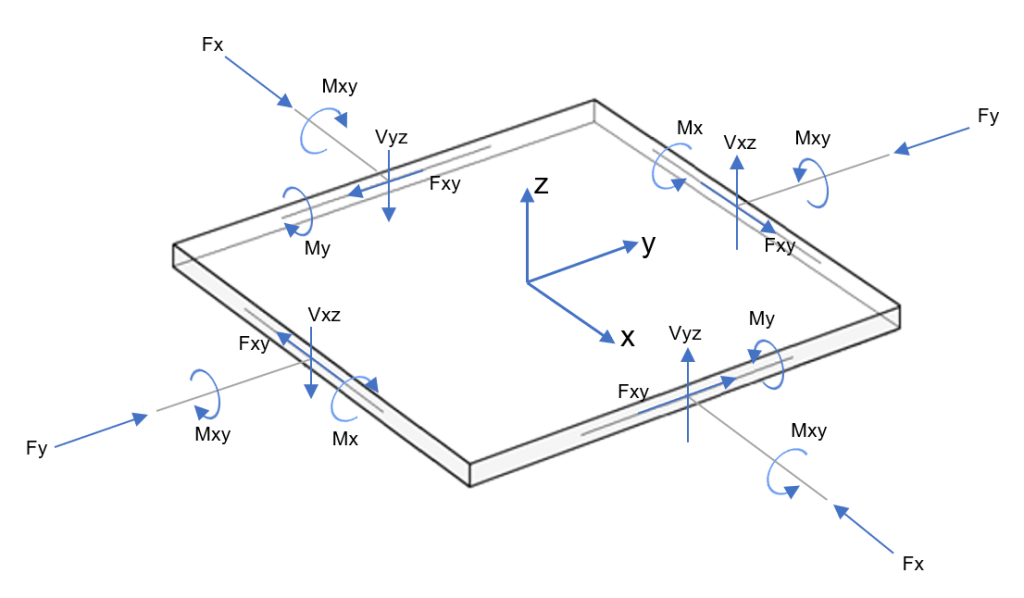
数字 3. 对板元素的操作 (弯矩和扭转力矩; 法向力和剪切力)
这个困难来自于实际要解决的问题是一个四阶偏微分方程,涉及两个方向的弯曲. 这个方程的形状是:
\(\压裂{\部分^4{w}}{{\部分的}{x^4}} + {2}\压裂{{\部分^4}{w}}{{{\部分的}{x^2}}{{\部分的}{y^2}}}+\压裂{\部分^4{w}}{{\部分的}{x^4}}-\压裂{f_z}{d} = 0\)
其中板刚度 (利用弹性机械和几何特性) 是 \(D=\frac{{Ë}{t^3}}{{12}{(1-\没有^2)}}\).
该方程的解析解仅适用于简单的支撑条件. 获得实际案例的可能解决方案的唯一方法是通过有限元法等数值方法.
SkyCiv 使用这种方法来解决板分析. 在以下链接上, 您将可以访问教程来了解 SkyCiv 平台特性: S3D 板设计 和 如何对板进行建模? .
如果你是 SkyCiv 的新手, 自行注册并测试软件!


