符合AS的单桩设计 2159 (2009) & 3600 (2018)

在高侧向负载或不利土壤条件下, 桩基础比浅基础更可取. 可以尝试诸如土壤改良方法以避免堆积, 然而, 这些方法可能涉及昂贵的过程, 在这种情况下, 堆甚至更便宜.

SkyCiv Foundation Design模块包括符合美国混凝土协会设计的桩 (ACI 318) 和澳大利亚标准 (如 2159 & 3600).

想要试用SkyCiv的Foundation Design软件? 我们的免费工具允许用户执行负载计算，而无需任何下载或安装!

基础设计计算器

设计桩的岩土强度

施加在桩上的垂直载荷由桩的端部承载力以及沿其长度方向的蒙皮或竖井摩擦力承担. 设计岩土强度 ([R_d,G) 等于极限岩土强度 ([R_d,和) 乘以岩土折减系数 (ø_G) 如上所指定 如 2159 部分 4.3.1.

\({[R}_{d,G} = {ø}_{G} × {[R}_{d,和}\) (1)

[R_d,G =设计岩土强度

[R_d,和 =极限岩土强度

ø_G =岩土折减系数

极限岩土强度 ([R_d,和)

极限土力强度等于桩的表皮摩擦系数之和 (F_米,s ) 乘以侧面表面积和基极电阻乘以桩尖的横截面积.

\( {[R}_{d,和} = [{[R}_{s} × ({F}_{米,s} × {一个}_{s} )] + ({F}_{b} × {一个}_{b} )\) (2)

[R_s =轴阻力的减小系数

F_米,s =轴摩擦阻力

一个_s =侧面表面积

F_b =基本电阻项

一个_b =桩尖的横截面积

有关更详细的指南, 看看我们有关计算的文章 皮肤摩擦阻力和承重能力.

岩土折减系数 (ø_G)

岩土工程折减系数是针对最终设计的基于风险的计算，其中考虑了不同的因素, 例如现场条件, 桩设计, 和安装因素. 其值通常在 0.40 至 0.90. 如 2159 4.3.1 还说明了如何估算其值，如等式​​所示 (3).

\( {ø}_{G} = {ø}_{b} + [K× ({ø}_{tf} – {ø}_{b})] ≥ {ø}_{b} \) (3)

ø_b =基本岩土强度折减系数

ø_tf =内在测试因子

K =测试收益因子

内部测试和测试受益因素均取决于桩上使用的载荷测试的类型. 它们的值在表中指定 1 和方程 (4) 和 (5). 本节将简要讨论桩的载荷测试 8 的AS 2159.

内在测试因子 (øtf)
静态负载测试	0.90
快速负载测试	0.75
预制桩的动态载荷测试	0.80
预制桩以外的动载荷测试	0.75
双向负载测试	0.85
没有测试	0.80

桌子 1: 内在测试因子值

静态负载测试的测试优势因子:

\( K = 分数{1.33 ×p}{p + 3.3} ≤ 1\) (4)

动态负载测试的测试优势因子:

\( K = 分数{1.13 ×p}{p + 3.3} ≤ 1\) (5)

p =已测试并符合验收标准的全部桩的百分比

基本岩土工程强度折减系数使用本节中讨论的风险评估程序进行评估 4.3. 的AS 2159. 所述程序的结果是个人风险评级 (内部收益率) 和总体设计的平均风险等级 (ARR) 用来确定ø的值_b 如表所示 2.

基本岩土强度折减系数 (øb)
平均风险等级 (ARR)	风险类别	øb 用于低冗余系统	øb 用于高冗余系统
ARR≤ 1.5	非常低	0.67	0.76
1.5 < ARR≤ 2.0	从低到低	0.61	0.70
2.0 < ARR≤ 2.5	低的	0.56	0.64
2.5 < ARR≤ 3.0	低至中度	0.52	0.60
3.0 < ARR≤ 3.5	中等	0.48	0.56
3.5 < ARR≤ 4.0	中到高	0.45	0.53
4.0 < ARR≤ 4.5	高的	0.42	0.50
ARR > 4.5	很高	0.40	0.47

桌子 2: 基本岩土折减系数值, (如 2159 桌子 4.3.2)

低冗余系统是重载的单桩，而高冗余系统包括大桩帽下的大桩组或具有大于 4 堆.

设计结构强度

桩的结构设计几乎与立柱相同. 设计结构强度 ([R_d,s) 需要最终的能力, 例如轴向力和剪力, 和弯矩. 混凝土桩的设计结构强度等于极限设计强度 ([R_我们) 降低强度降低因子 (ø_s) 和具体的放置系数 (ķ), 如本节所述 5.2.1 的AS 2159.

\( {[R}_{d,s} = {ø}_{s} ×k× {[R}_{我们} \) (6)

ø_s =强度降低系数

k =混凝土放置系数

[R_我们 =终极设计实力

强度降低系数的值显示在表中 3. 具体的放置系数范围为 0.75 至 1.0, 取决于桩的施工方法. 然而, 用于混凝土和水泥浆以外的桩, k应取为 1.0.

强度降低因素 (ø)
轴向力不弯曲	0.65
无轴向力弯曲 (ø铅)	0.65 ≤ 1.24 – [(13 ×kuo)/12] ≤ 0.85
轴向压缩弯曲:
(一世) ñü ≥Nub	0.60
(ii) ñü < ñub	0.60 + {(ø铅 – 0.66) × [1 – (ñü/ñub)]}
剪力	0.70

桌子 3: 强度降低因素 (桌子 2.2.2, 如 3600-18)

单桩的轴向和挠曲能力

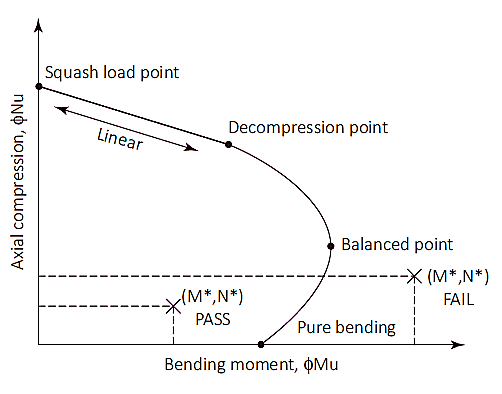
类似于列, 桩也可能同时承受压缩和弯曲载荷. 使用相互作用图检查轴向和弯曲能力. 该图是从纯弯曲点到达到平衡点的载荷增加所引起的弯曲和轴向载荷行为的直观表示。.

 

数字 1: 列交互图

壁球负荷 (ñ_uo)

压弯载荷点是图上纯压桩将失败的点. 这一点, 轴向载荷施加在截面的塑料质心上，以保持压缩状态而不会弯曲. 壁球负荷 (ñ_uo) 和塑料质心的位置 (d_q) 如方程式所示进行计算 (7) & (8). 虽然塑料质心的位置可以视为 1/2 具有对称钢筋布置的对称截面的总横截面深度.

\( {ϕN}_{uo} =ø× [({一个}_{G} – {一个}_{s}) × ({一种}_{1} ×f’c) + ({一个}_{s} × {F}_{他的})] \) (7)

一个_G =总横截面积

一个_s =钢铁总面积

一种₁ = 1.0 – (0.003 ×f’c) [0.72 ≤α₁ ≤0.85]

f’c =混凝土强度

F_他的 =钢的屈服强度

\( {d}_{q} = 分数{[(b×D) – {一个}_{s}] × ({一种}_{1} ×f’c) × sum_{i = 1}^{ñ} ({一个}_{与一个} × {F}_{他的} × {d}_{yi})}{{ñ}_{uo}} \) (8)

b =桩横截面宽度

D =桩的横截面深度或直径

一个_与一个 =正在考虑的钢筋面积

d_yi =考虑钢筋的深度

压入点到减压点

减压点是极限压缩纤维处的混凝土应变等于 0.003 极端拉伸纤维中的应变为零. 可以通过具有强度折减系数的线性插值来计算壁球载荷与减压点之间的桩的强度 (ø_s) 的 0.6.

减压点到纯弯曲

纯弯曲点是轴向载荷为零的位置. 从减压点到纯弯曲的过渡使用的强度折减系数为 0.6 至 0.8 和一个输入参数 (ķ_ü) 介绍. k的值_ü 开始于 1 在减压点处减小，直到达到纯弯曲为止. 两点之间的过渡, 达到平衡的状态. 这一点, 混凝土应变达到极限 (Ë_C= 0.003) 外钢应变达到屈服 (Ë_s= 0.0025), k的值_ü 此时大约 0.54 强度降低系数为 0.6.

一次值为k_ü 被选中, 可以计算截面的拉伸和压缩力. 截面上的轴向载荷等于拉伸力和压缩力的总和, 而弯矩是通过解决这些绕中性轴的力来计算的. 压缩力和拉力的计算方法如下

因混凝土而受力 (F_抄送):

\( {F}_{抄送} = {一种}_{2} ×f’c× {一个}_{C} \) (9)

一种₂ = 0.85 – (0.0015 ×f’c) [一种_{2 ≥}0.67]

一个_C =压缩块面积 (参考图 2)

= b ×γ×k_ü ×d (矩形截面)

=(1/2) × (θ – 正弦θ) × (D / 2)² (圆形截面)

γ= 0.97 – (0.0025 ×f’c) [C _≥0.67]

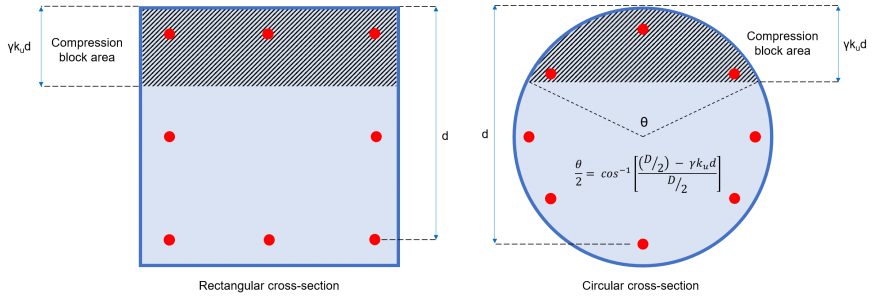
数字 2: 混凝土压块面积

力量 (F_和) 和时刻 (中号_一世) 由每个酒吧贡献:

型材的每个钢筋都会施加可能是压缩力或拉伸力的力, 取决于值栏应变 (Ë_和) 等式中显示 (10).

\( {Ë}_{和} = frac{{Ë}_{C}}{({ķ}_{ü} ×d)} × [({ķ}_{ü} ×d) – {d}_{yi}] \) (10)

d_yi =所考虑钢筋的深度

Ë_C=混凝土应变= 0.003

如果ε_和 < 0 (酒吧处于紧张状态)

如果ε_和 > 0 (条处于压缩状态)

压缩酒吧:

\( {F}_{和} = {σ}_{和} × {一个}_{与一个} \) (11)

σ_和 =应力（以巴为单位）= 最低限度 [(Ë_和 × Ë_s ), F_他的]

Ë_s =钢的模量弹性

一个_与一个 =酒吧面积

张力杆:

\( {F}_{和} = [{σ}_{和} – ({一种}_{2} ×f’c)] × {一个}_{与一个} ≥ 0\) (12)

σ_和 =应力（以巴为单位）= 最低限度 [(Ë_和 × Ë_s ), –F_他的]

Ë_s =钢的模量弹性

一个_与一个 =酒吧面积

每个酒吧的时刻:

\( {中号}_{一世} = {F}_{和} × {d}_{yi} \) (13)

桩的轴向容量:

\( {小岛}_{ü} =ø× [ {F}_{抄送} + {Σ}_{i = 1}^{ñ} {F}_{和}]\) (14)

桩的抗弯能力:

\( {疮}_{ü} =ø× [ ({ñ}_{ü} × {d}_{q}) – ({F}_{抄送} × {和}_{C}) – {Σ}_{i = 1}^{ñ} {中号}_{一世}] \) (15)

设计弯矩:

部分 7.2 指定在水平放置桩时要求桩的位置偏移公差为75mm. 此要求可能会产生等于轴向载荷乘以75mm偏心距的弯矩. 另外, 还应考虑一个最小设计力矩，该力矩等于轴向力乘以 5% 桩的总最小宽度的. 因此, 设计弯矩应为公式16a和16b之间的较大值.

\( {中号}_{d} = {{中号}^{*}}_{已应用} + ({ñ}^{*} × 0.075 米) \) (16一个)

\( {中号}_{d} = {ñ}^{*} × (0.05 ×D) \) (16b)

中号_d =设计弯矩

M *_已应用 =施加力矩

N * =轴向载荷

D =桩宽

单桩剪切力

抗剪强度的计算应符合本节的规定。 8.2 的AS 3600. 剪切强度等于混凝土和钢筋的组合剪切能力 (方程 17).

\( {øV}_{ü} =ø× ({V}_{uc} + {V}_{我们}) ≤ {øV}_{ü,最高} \) (17)

混凝土的抗剪强度 (V_uc)

如方程式所示，计算混凝土对剪切能力的贡献 (18) 在章节中定义 8.2.4.1 的AS 3600. 本部分还要求√f’c的值不得超过 9.0 兆帕. 参数k的值_v 和 θ_v 通过使用本节建议的简化方法确定 8.2.4.3 的AS 3600.

\( {V}_{uc} = {ķ}_{v} ×b× {d}_{v} × sqrt{f’c} \) (18)

d_v =有效剪切深度= 最大 [(0.72 ×D ), (0.90 ×d )]

确定抗剪钢筋的最小面积 (一个_sv.min) & ķ_v:

抗剪钢筋面积 (一个_sv) 是在所施加载荷的相同方向上绑在一起的所有提供的钢筋的总钢筋面积. 部分 8.2.1.7 的AS 3600 提供了最小横向剪切钢筋的方程式, 应该是:

\( \压裂{{一个}_{sv.min}}{s} = frac{0.08 × sqrt{f’c} ×b}{{F}_{syf}} \)

F_syf =抗剪钢筋的屈服强度

s =抗剪钢筋的中心间距

对于 (一个_sv/s) < (一个_sv.min/s):

\( {ķ}_{v} = frac{200}{[1000 + (1.3 × {d}_{v} )]} ≤ 0.10\)

对于 (一个_sv/s) ≥ (一个_sv.min/s):

\( {ķ}_{v} = 0.15 \)

钢筋的抗剪强度 (V_我们)

等式中显示了横向抗剪钢筋对计算的抗剪承载力的贡献 (19), 本节中定义 8.2.5 的AS 3600.

\( {V}_{我们} = frac{{一个}_{sv} × {F}_{syf} × {d}_{v}}{s} ×婴儿床{θ}_{v} \) (19)

θ_v=压杆的倾斜角度=36º

最大抗剪强度 (V_最大)

剪切能力是有限的，在任何情况下都不得超过本节规定的最大值 8.2.6 的AS 3600 (方程 20).

\( {V}_{最大} = 0.55 × [ (f’c×b× {d}_{v}) × frac{婴儿床{θ}_{v} + 婴儿床{一种}_{v}}{1 + 婴儿床^{2}{θ}_{v} }] \) (20)

一种_v=倾斜抗剪钢筋与纵向抗拉钢筋之间的角度≈90º

极限剪切强度 (V_ü)

混凝土和抗剪钢筋贡献的总抗剪强度应小于或等于V的极限值_最大

\( {V}_{ü} = ({V}_{uc} + {V}_{我们} ) ≤ {V}_{最大} \) (21)

设计抗剪强度 (øV_ü)

极限抗剪强度应采用的容量减小系数为ø= 0.7. 因此, 桩的设计抗剪强度由下式给出：:

\( {øV}_{ü} =ø× ({V}_{uc} + {V}_{我们} ) \) (22)

参考资料

• 盒, 朗尼 (2018). 澳大利亚结构工程师指南. CRC出版社.
• 打桩设计与安装 (2009). 如 2159. 澳大利亚标准
• 混凝土结构 (2018). 如 3600. 澳大利亚标准