在钢连接设计中, 螺栓 通常被设计成一个螺栓组,作为一个整体来抵抗给定的载荷. 螺栓组的强度通常通过其最关键螺栓的控制强度来计算. 直接载荷分布在螺栓总数中, 而由于负载偏心引起的感应力矩分布与螺栓组的惯性矩和距质心的距离有关. 这种分析称为弹性分析. 由于其对负载分布的简化和保守假设, 它通常会产生过度设计的螺栓连接.
在谈论价值工程和经济设计时, 大多数制造商更喜欢非弹性方法. 对于相同大小的载荷,它需要较少数量的螺栓. 做无弹性的方法, 瞬时旋转中心 (ICOR) 使用迭代的方法是最好的方法.
在这篇文章中, 我们将演示如何计算a的强度 螺栓连接 使用 ICOR 方法. 每个螺栓的反应将使用公式计算 (7-1) 在页面上 7-7 的 AISC第15版手册. 这将用于检查螺栓组瞬时中心的假定位置是否正确. 最后, 一旦我们有了正确的 IC 位置, 然后我们将计算螺栓组系数 C 以确定其强度.
使用ICOR方法获取螺栓组系数是一个漫长的过程,因为它需要通过试错法来获取瞬时中心 (我知道了) 位置. 如今, 使用计算机求解器, 螺栓组的 IC 可以使用编程迭代轻松计算. SkyCiv 螺栓组求解器 使用快速迭代方法在几秒钟内确定 IC 位置和螺栓组系数. 目前在AS中实现 4100 设计代码,但很快就会集成到其余的设计代码中.
获取螺栓组属性
让我们开始对一个由四个螺栓组成的螺栓组进行简单分析,该螺栓组承受的偏心垂直剪切载荷为 10 ps. 载荷沿 x 轴的偏心率为 4 英寸到螺栓组的右侧. 与垂直方向的角度为零,沿 y 轴的偏心率为零.
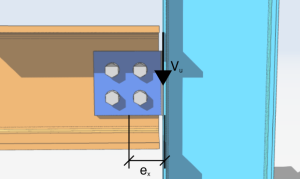
\(V_{ü} = 10 基普 \)
\(\θ = 0 度)
\(e_{X} = 4 在)
\(e_{和} = 0英寸)
首先要做的是获取我们螺栓组中所有螺栓的坐标. 强烈建议使用视觉指南和表格.
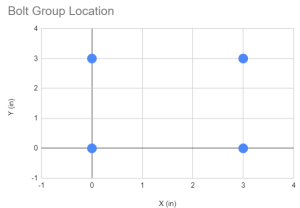
| 店铺编号 | X (在) | 和 (在) |
| 1 | 0 | 0 |
| 2 | 0 | 3 |
| 3 | 3 | 0 |
| 4 | 3 | 3 |
沿 x 获得螺栓组的质心- 和 y 轴, 我们需要下面的公式.
让 \(ñ \) = 螺栓总数
\(X_{CG} = frac{\总和}{ñ}\)
\(Y_{CG} = frac{\总和}{ñ} \)
然后, 我们的解决方案是:
\(X_{CG} = frac{\总和}{ñ} = frac{0 在 + 0 在 + 3 在 + 3 在}{4} = 1.5 在)
\(Y_{CG} = frac{\总和}{ñ} = frac{0 在 + 3 在 + 0 在 + 3 在}{4} = 1.5 在)
假设 I.C 的位置.
得到质心后, 我们将假设瞬时中心的位置 \(我知道了). 作为第一次尝试, 我们可以假设 IC 位于螺栓组的几何质心.
所以, 认为
\(X_{我知道了} = X_{CG} = 1.5 在)
\(Y_{我知道了} = Y_{CG} = 1.5 在)
然后, 我们将每个螺栓的位移与 IC 的位置制成表格. 我们可以通过首先获取沿 x 的距离和沿 y 的距离来简单地做到这一点, 然后得到它的位移
| 店铺编号 | CX (在) | cy (在) | C (在) |
| 1 | -1.5 | -1.5 | 2.121 |
| 2 | -1.5 | 1.5 | 2.121 |
| 3 | 1.5 | -1.5 | 2.121 |
| 4 | 1.5 | 1.5 | 2.121 |
在哪里,
\(C_{X} = X_{一世} – X_{我知道了}\)
\(C_{和} = Y_{一世} – Y_{我知道了}\)
\(c = sqrt{{\剩下(C_{X} \对)}^{2} + {\剩下(C_{和} \对)}^{2}}\)
对于螺栓号. 1, 我们的解决方案是
\(C_{X} = 0 英寸 – 1.5 在 = -1.5 在)
\(C_{和} = 0 英寸 – 1.5 在 = -1.5 在)
\(c = sqrt{{\剩下( -1.5 在右)}^{2} + {\剩下( -1.5 在右)}^{2}} = 2.121in\)
计算每个螺栓与 IC 距离的变形
所以, 从假定的 IC 位置获取螺栓距离后, 然后我们计算每个螺栓的变形作为其距离的函数.
每个螺栓的最大变形, 设置 \(\三角洲_{最高} = 0.34 在), 基于 ASTM 螺栓的实验数据,如 AISC 页面中所述 7-8. 通过使用线性比例, 和设置 \(\三角洲_{最高} = 0.34 在), 我们可以计算单个螺栓相对于其最大距离的部分的变形 \(C_{最高}\). 得到的方程 如下所示.
\(\三角洲_{1} = 0.34in times left( \压裂{C}{C_{最高}}\对) \)
对于螺栓号. 1, 变形是
\(\三角洲_{1} = 0.34in times left( \压裂{2.121 在}{2.121 在}\对)\)
对于其余的螺栓, 计算的变形如下表所示.
| 店铺编号 | \(\Delta\) (在) |
| 1 | 0.34 |
| 2 | 0.34 |
| 3 | 0.34 |
| 4 | 0.34 |
获取每个螺栓的反应
一旦我们有了每个螺栓的变形, 然后我们可以使用 AISC 15th Ed. 情商 (7-1) 得到每个螺栓的反应.
\(R = R_{超} \剩下 ( 1 – e^{-10\三角洲}\对 )^{0.55}\)
的 \(R_{超}\) 等式中是螺栓上的假定极限载荷, 我们可以将其设置为螺栓剪切强度.
\(R_{超} = phi R_{ñ} \)
对于我们的例子, 我们将使用螺栓抗剪强度为 \(24.4 基普). 也允许使用其他值,因为当我们计算螺栓组系数时这将抵消 \(C) 稍后的.
对于螺栓号. 1, 计算的反应是
\(R = R_{超} \剩下 ( 1 – e^{-10\三角洲}\对 )^{0.55}\)
\(R = 24.4 基普左 ( 1 – e^{-10 \时代左 ( 0.34 在右 )}\对 )^{0.55}\)
\(R = 23.949 基普)
对于其余的螺栓, 计算的反应如下. 与此同时, 螺栓反应的成分 \(R) 沿 x 和 y 也显示.
| 店铺编号 | [R (基普) | 接收 (基普) | 瑞 (基普) |
| 1 | 23.949 | 16.937 | -16.937 |
| 2 | 23.949 | -16.937 | 16.937 |
| 3 | 23.949 | 16.937 | -16.937 |
| 4 | 23.949 | -16.937 | 16.937 |
| ⅀Rx = 0 | ⅀Ry = 0 |
用于 1 号螺栓, 获取 x 和 y 分量的解决方案如下所示.
\(R_{X} = -R 左 ( \压裂{C_{和}}{C} \对 ) = -23.949 \时代左 ( \压裂{-1.5在}{2.121在} \对 ) = 23.949 基普)
\(R_{和} = R 左 ( \压裂{C_{X}}{C} \对 ) = 23.949 \时代左 ( \压裂{1.5在}{2.121在} \对 ) = 23.949 基普)
此外, 由于偏心,我们应该得到每个螺栓的诱导力矩载荷. 计算这个, 我们使用组件 \(R_{X}\) 和 \(R_{和}\) 并将它们与怪癖相乘 \(C_{和}\) 和 \(C_{X}\), 分别.
用于 1 号螺栓, 对 IC 的瞬间反应是
\(M_{[R} = -R_{X}C_{和} + -R_{和}C_{X} \)
\(M_{[R} = -16.937 基普次左 ( -1.5在右) + -16.937 基普次左 ( -1.5 在右 ) \)
\(M_{[R} = 50.811 鸡进)
对于其余的螺栓, 相应的矩反应列于下表.
| 店铺编号 | 先生 (小鸡) |
| 1 | 50.811 |
| 2 | 0 |
| 3 | 0 |
| 4 | 50.811 |
| ⅀先生 = 101.622 |
验证 IC 位置
现在我们有了每个螺栓的剪切和力矩反应, 我们将使用它来确定该螺栓组抵抗的 Pu 负载量. 去做这个, 我们将得到沿 x 的所有反应之和和沿 y 的所有反应之和的结果.
从上一节, 我们已经计算出
\(\总和R_{X}=0kip\)
和
\(\总和R_{和}=0kip\)
所以,
\(P_{ü} = sqrt{{\剩下( \总和R_{X} \对)}^{2} + {\剩下( \总和R_{和} \对)}^{2}} = 0 基普)
由于产生的负载 \(P_{ü} = 0基普), 我们现在可以决定不进行验证,因为我们的数据将为零. 我们还可以推断出 I.C. 的第一个假设位置。, 位于螺栓组的质心, 是不正确的. 然而, 出于本次讨论的目的, 我们将继续执行以下步骤.
\(P_{用户体验} = -P_{ü}罪左 ( \θ对 ) = 0 基普 \)
\(P_{你} = -P_{ü}因为左 ( \θ对 ) = 0 基普 \)
\(M_{ü} = -P_{用户体验}\剩下 ( Y_{CG} + e_{和} – Y_{我知道了} \对 ) + -P_{你} \剩下 (X_{CG} + e_{X} – X_{我知道了} \对 ) = 0 基普 \)
以来,
\(P_{用户体验} \neq sum R_{X} \)
\(P_{你} \neq sum R_{和} \)
\(M_{ü} \我不是M_{[R} \)
因此, I.C 的假定位置. 是不正确的. 我们现在可以继续下一个假定的位置.
SkyCiv 已将螺栓组计算完全集成到澳大利亚标准模块中. 想试用我们的连接设计软件?
第二次迭代
对于我们的第二次迭代, 让我们假设 I.C. 位于下图坐标.
认为
\(X_{我知道了} = 0.062 在)
\(Y_{我知道了} = 1.5 在)
然后, 让我们执行我们在第一次迭代中执行的步骤. 综上所述, 下表将显示坐标, 每个螺栓与假定 I.C 的距离, 以及相对于距离的相应变形.
| 店铺编号 | X (在) | 和 (在) | CX (在) | cy (在) | C (在) | \(\Delta\) (在) |
| 1 | 0 | 0 | -0.062 | -1.5 | 1.501 | 0.155 |
| 2 | 0 | 3 | -0.062 | 1.5 | 1.501 | 0.155 |
| 3 | 3 | 0 | 2.938 | -1.5 | 3.299 | 0.34 |
| 4 | 3 | 3 | 2.938 | 1.5 | 3.299 | 0.34 |
请注意,计算出的质心 螺栓组 仍然相同,因为螺栓坐标没有任何变化.
\(X_{CG} = 1.5 在)
\(Y_{CG} = 1.5 在)
然后, 我们计算沿 x 的反应, 沿 y 的反应, 和相应的时刻. 数值如下表所示.
| 店铺编号 | [R (基普) | 接收 (基普) | 瑞 (基普) | 先生 (小鸡) |
| 1 | 21.4 | 21.4 | -0.9 | 32.1 |
| 2 | 21.4 | -21.4 | -0.9 | 32.1 |
| 3 | 23.9 | 10.9 | 21.3 | 79.0 |
| 4 | 23.9 | -10.9 | 21.3 | 79.0 |
| ⅀Rx = 0 | ⅀Ry = 41 | ⅀先生 = 222 |
下一个, 我们确定沿 x 和 y 的所有反应的合成载荷.
\(P_{ü} = sqrt{{\剩下( \总和R_{X} \对)}^{2} + {\剩下( \总和R_{和} \对)}^{2}}\)
\(P_{ü} = sqrt{{\剩下( 0 基普右)}^{2} + {\剩下( 40.703 基普右)}^{2}}\)
\(P_{ü} = 40.703 基普)
然后, 基于给定的合成载荷的分量 \(\theta ) 如下所示.
\(P_{用户体验} = -P_{ü}罪左 ( \θ对 ) = -41kip times sin left ( 0 度右 )= 0 基普)
\(P_{你} = -P_{ü}因为左 ( \θ对 ) = -41kip times cos left ( 0 度右 )= -41 基普)
然后,我们将使用这些组件来求解关于假定 I.C 的力矩负载.
\(M_{ü} = -P_{用户体验} \剩下 ( Y_{CG} + e_{和} – Y_{我知道了} \对) + P_{你} \剩下 ( X_{CG} + e_{X} – X_{我知道了} \对)\)
\(M_{ü} = -0 基普左 ( 1.5 在 +0 在 – 1.5 在右) + 41 基普左 ( 1.5 在 +4 在 – 0.06 在右)\)
\(M_{ü} = -222 鸡进)
下一个, 让我们比较计算的 P用户体验, P用户体验, 和 mü 对螺栓组的反应.
\(P_{用户体验} \大约 – \总和R_{X}\)
\(P_{你} \大约 – \总和R_{和}\)
\(M_{ü} \大约 – \总和 M_{ü}\)
因为等式的左边几乎等于右边, 我们可以说 I.C 的假定位置. 是正确的!
求解 C 系数
一旦 I.C. 位置确定, 我们现在可以用下面的公式得到螺栓组系数 C.
\(C = frac{P_{ü}}{\φR_{ñ}} = \frac{40.703 基普}{24.4 基普} = 1.668\)
免费螺栓组计算器
检查我们如何使用我们的方法通过这种方法设计螺栓连接 自由钢连接设计计算器! 更多功能, 立即注册我们的 Structural 3D 软件以开始使用!


