Dans cet article, nous allons vous montrer comment concevoir une poutre en béton armé à l'aide du logiciel SkyCiv. Ce tutoriel couvre deux options logicielles fournies par SkyCiv pour la conception de faisceaux: Le faisceau SkyCiv et la 3D structurelle. Nous approfondirons les deux outils pour vous aider à accéder et à concevoir efficacement les poutres. A la fin de l'article, nous appliquerons également la méthode des coefficients prescrite par ACI-318-19 pour la conception des poutres RC.
Si vous débutez dans la conception de poutres, nous vous recommandons de lire quelques articles d'introduction sur SkyCiv:
- Qu'est-ce que le béton armé?
- Comment calculer la résistance au moment de flexion pour une section de poutre?
- Comment analyser une poutre continue?
Ces tutoriels vous aideront à mieux comprendre le processus général de conception des poutres.
Si vous êtes nouveau chez SkyCiv, Inscrivez-vous et testez le logiciel vous-même!
Logiciel SkyCiv Beam
La première étape consiste à créer le modèle de faisceau dans le logiciel SkyCiv Beam. Nous indiquons les étapes nécessaires: (Entre parenthèses, nous montrons les données d'exemple):
- Sur la page du tableau de bord, sélectionner le module poutre.
- Créer une poutre définissant sa longueur (66 pi).
- Accédez aux supports et définissez des charnières ou des tiges simples (charnière au début et à la fin; tige aux troisièmes points).
- Allez dans les sections et créez-en une rectangulaire (section rectangulaire; largeur = 18 po; hauteur = 24 po).
- Sélectionnez ensuite le bouton de charge distribuée et attribuez-en un, deux, ou plus selon vos besoins (charge morte superposée = 0.25 kip/pi; charge vive = 0.40 kip/pi)
- L'étape suivante consiste à créer des combinaisons de charge (\({L_d = 1,2fois D + 1.6\fois L}\))
- Ensuite, résoudre le faisceau!
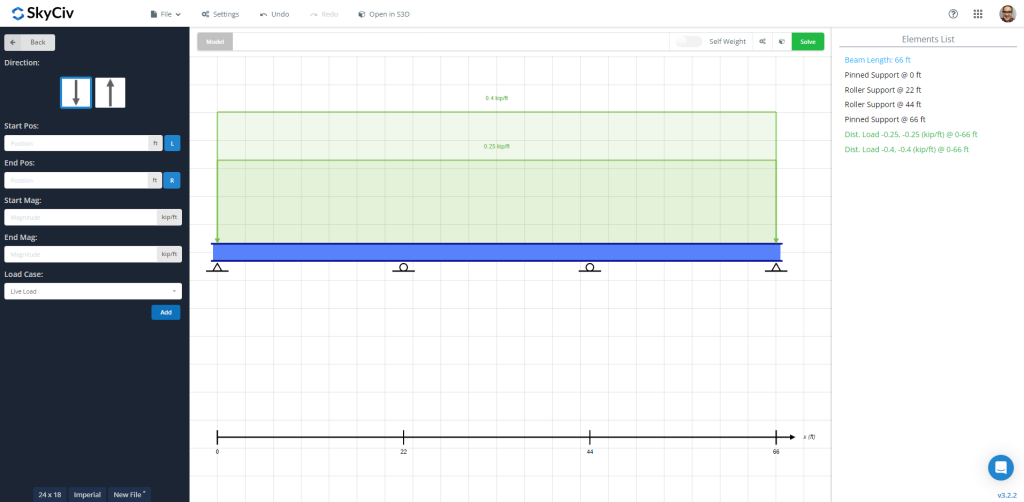
Figure 1: Modèle de poutre avec charges mortes et vives appliquées
Après avoir résolu le faisceau, nous pouvons vérifier les résultats, comme le diagramme de flexion, pour obtenir leurs valeurs maximales le long de la longueur de l'élément. Les images suivantes montrent la sortie finale.
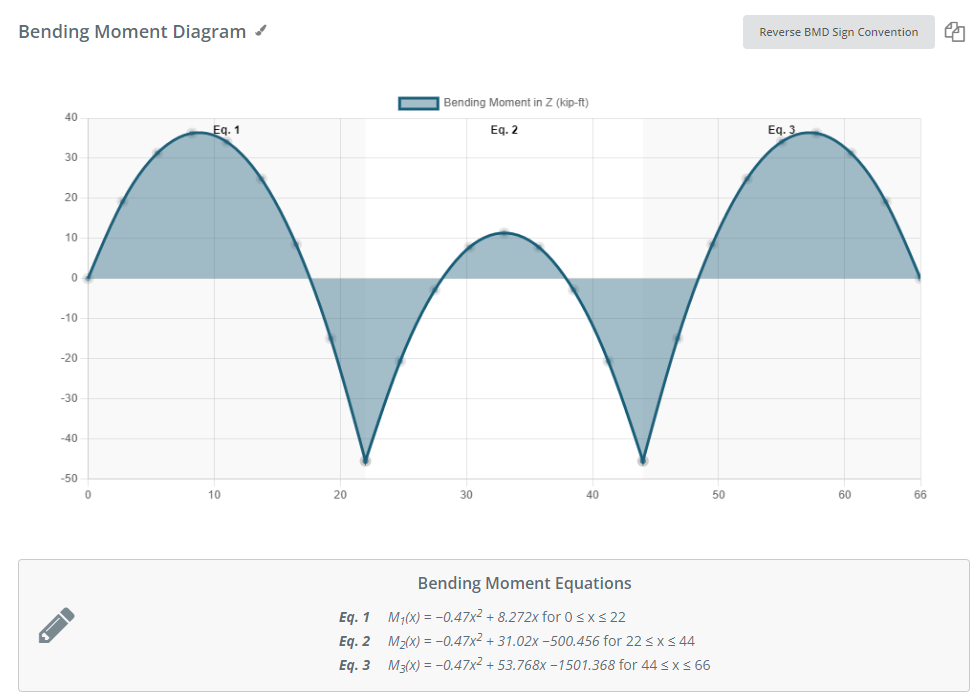
Figure 2: Diagramme de moment de flexion dû à la combinaison de charge spécifiée
Le logiciel SkyCiv Beam nous donne un tableau avec les valeurs maximales des forces, la contrainte interne, et déplacement:
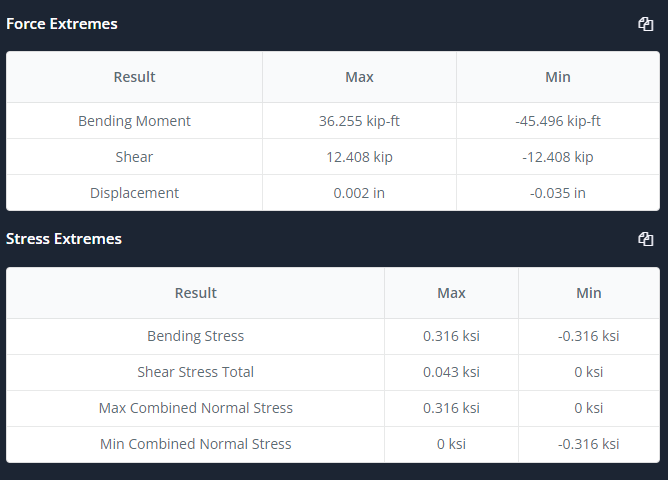
Figure 3: Sommaire
Il est maintenant temps de sélectionner l'onglet de conception et de sélectionner et de définir l'entrée en tant que disposition d'armature, sections d'analyse, quelques coefficients, combinaisons de charges, etc. Regardez les chiffres 4 et 5 pour plus de descriptif.
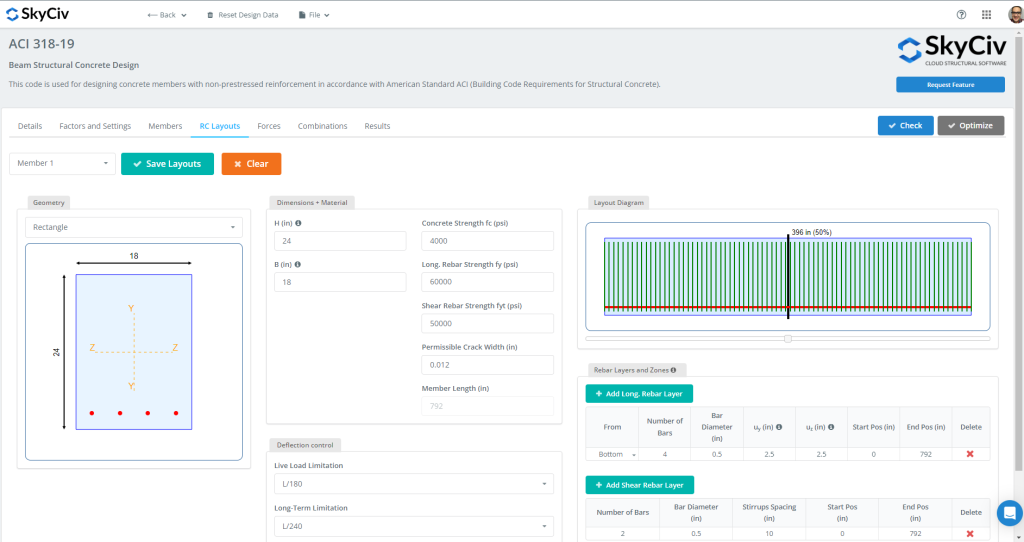
Figure 4: Dispositions des faisceaux RC
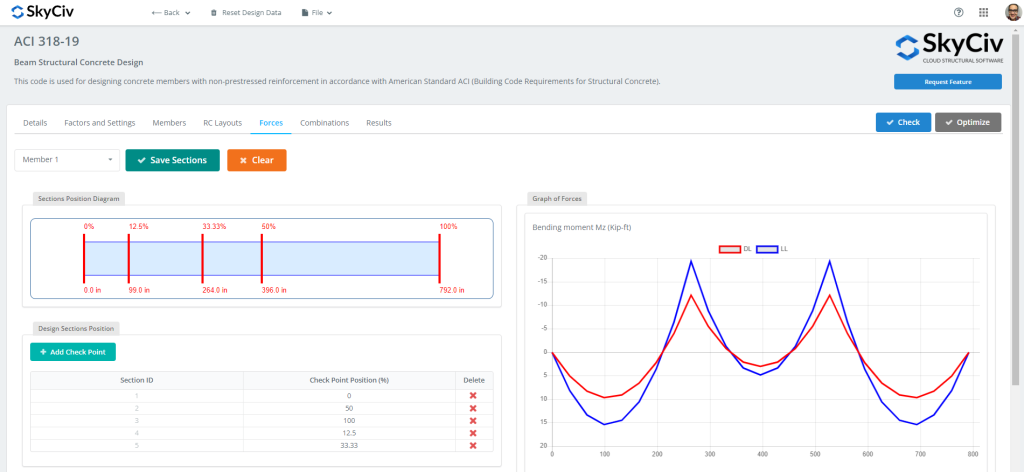
Figure 5: Forces et sections à évaluer lors de la conception
Une fois toutes les données prêtes, on peut cliquer sur “Vérifier” bouton. Cette action nous donnera alors les résultats et les ratios de capacité pour la résistance et la facilité d'entretien.
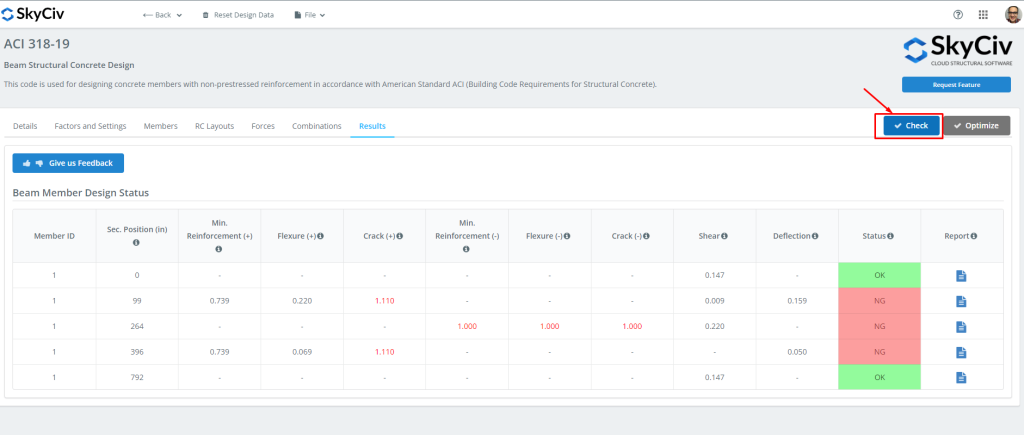
Figure 6: Résultats de conception du module de poutre.
Vous pouvez ensuite télécharger tous les rapports dont vous avez besoin pour!
Si vous êtes nouveau chez SkyCiv, Inscrivez-vous et testez le logiciel vous-même!
SkyCiv Structural 3D
Il est maintenant temps d'utiliser Structural 3D! Nous vous recommandons de revenir simplement au logiciel de faisceau et de cliquer sur le “Ouvrir dans S3D” bouton. Cela nous aidera à préparer le modèle et ses entrées en S3D.
Une fois que nous avons cliqué sur le bouton de modification, le modèle a été créé automatiquement. N'oubliez pas de le sauvegarder! (Si vous avez besoin de vous familiariser avec ce module, regarde ça lien tutoriel!)
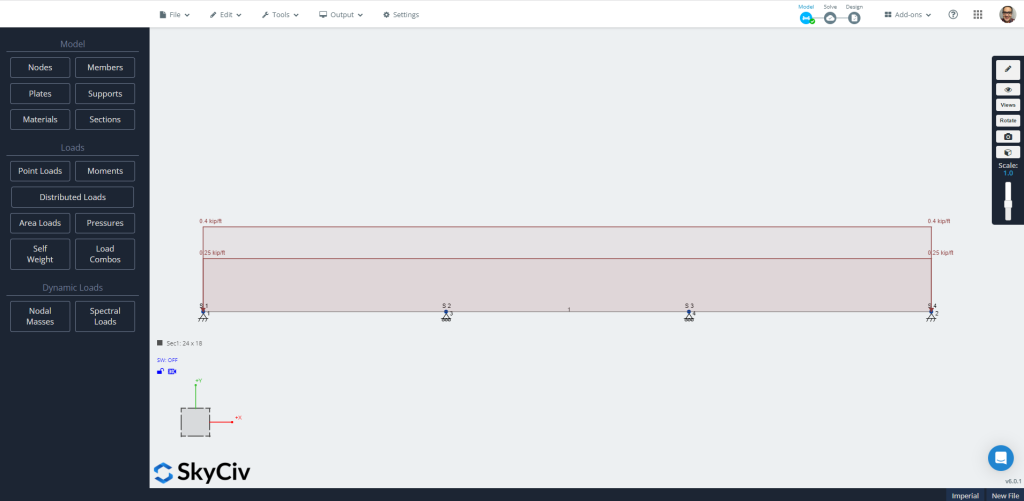
Figure 7: Modèle créé automatiquement en S3D.
Allez maintenant directement au “Résoudre” icône choisissant le “Analyse linéaire” option. N'hésitez pas à vérifier et comparer les résultats; nous utiliserons le “Conception” option. Il est temps de définir toutes les caractéristiques nécessaires pour évaluer le faisceau sur les différents onglets.
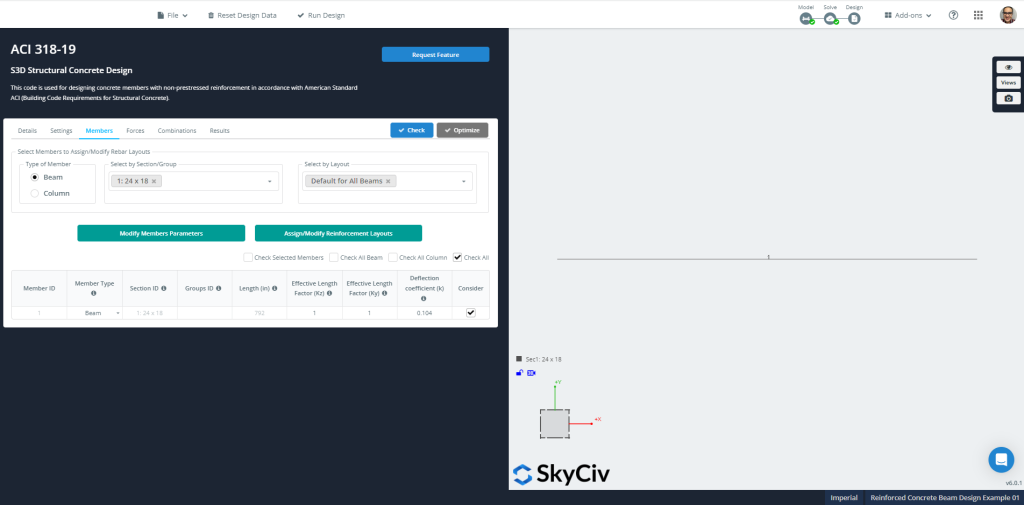
Figure 8: Membrures’ informations pour la conception
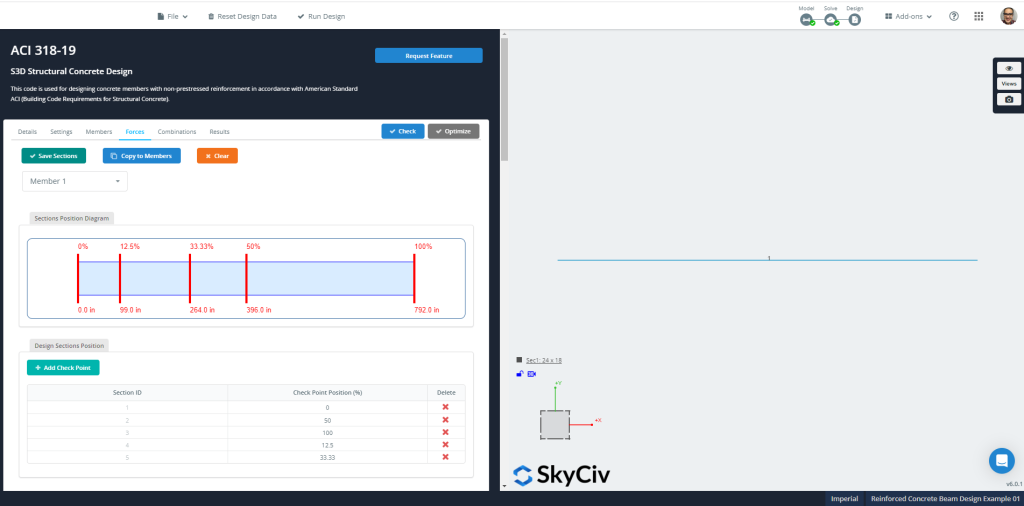
Figure 9: Membrures’ forces et sections pour la conception
SkyCiv peut vérifier une disposition RC définie particulière ou calculer une optimisation de renforcement de section. Nous aimerions vous suggérer d'exécuter cette dernière option.
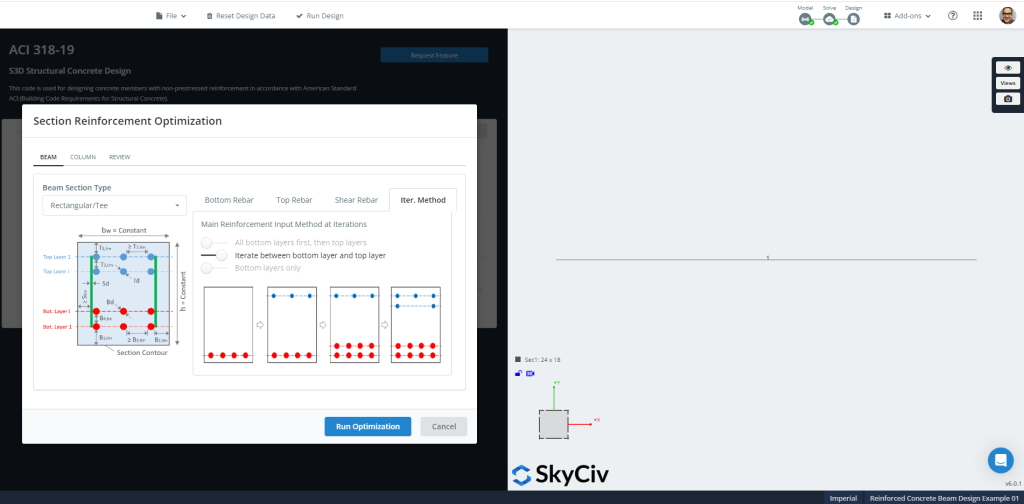
Figure 10: Optimisation du renforcement de section.
Les figures 11 et 12 montrer le résultat final et le ferraillage de section suggéré calculé pour la conception d'optimisation.
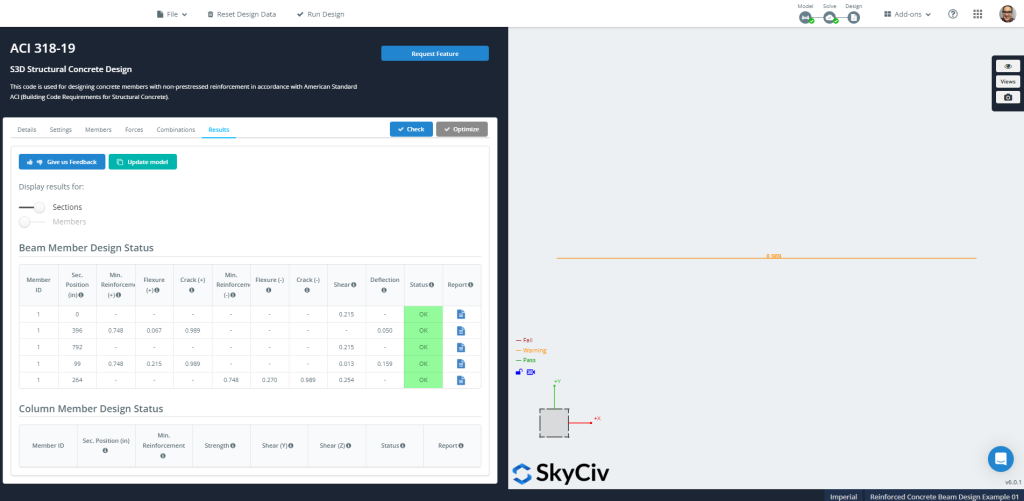
Figure 11: Résultats de la conception structurelle en béton
Vous pouvez ensuite télécharger tous les rapports dont vous avez besoin pour!
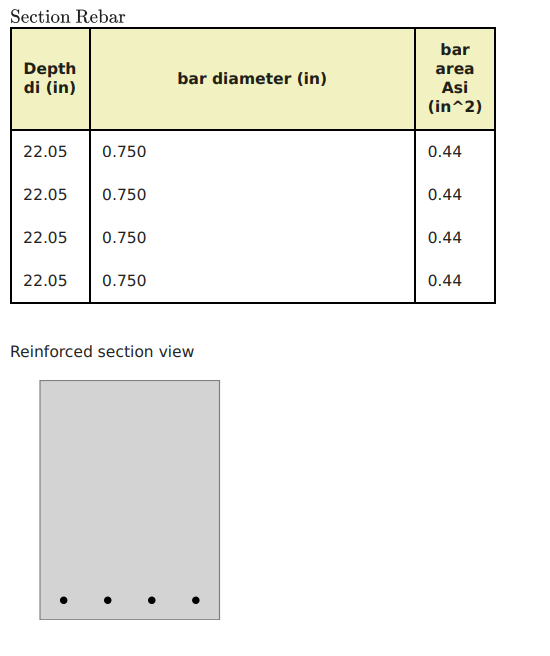
Figure 12: Optimisation dans l'acier d'armature de section
Si vous êtes nouveau chez SkyCiv, Inscrivez-vous et testez le logiciel vous-même!
ACI-318 Équations approximatives
Lors de la conception d'une poutre continue, ACI-318 permet d'utiliser des coefficients de moment pour les calculs de flexion. (Pour plus d'exemples, n'hésitez pas à visiter ces articles de SkyCiv sur Conception de dalle)
Les moments aux sections critiques sont calculés avec: \( M_u = coefficient times w_u times l_n^2 \). Où le coefficient peut être obtenu à partir de ce qui suit:
- Portée extérieure:
- Extérieur négatif: \(\frac{1}{16}\)
- Intervalle positif: \(\frac{1}{14}\)
- Intérieur négatif:\(\frac{1}{10}\)
- Portée intérieure:
- Négatif: \(\frac{1}{11}\)
- Intervalle positif: \(\frac{1}{16}\)
Nous sélectionnerons deux cas: la valeur maximale absolue pour les moments de flexion positifs et négatifs.
\(wu=1.2fois D + 1.6\fois L = 1.2 \fois 0.25 + 1.6 \fois 0.4 = 0.94 \frac{kip}{pi} \)
\(M_{u,négatif} = {\frac{1}{10}}{\fois 0.94 {\frac{kip}{pi}}}{\fois {(22 pi)}^ 2} = 45.50 {kip}{pi} \)
\(M_{u,position} = {\frac{1}{14}}{\fois 0.94 {\frac{kip}{pi}}}{\fois {(22 pi)}^ 2} = 32.50 {kip}{pi} \)
Calcul de la résistance à la flexion pour moment négatif, \({M_{u,négatif} = 45.50 {kip}{pi}}\)
- Section présumée à tension contrôlée. \({\phi_f = 0.9}\)
- Largeur du faisceau, \({b=18 po}\)
- Zone de renfort en acier, \({A_s = frac{M_u}{\phi_ffois 0,9dfois fy}= frac{45.50 kip-ft times 12 en -ft }{0.9\fois 0.9(17 in )\fois 60 KSI}=0,66 {in}^ 2}\)
- \({\rho_{min} = 0.003162}\). Zone d'armature minimale en acier, \({UNE_{s,min}=rho_{min}\fois bfois d = 0.003162 \fois 18 en temps 17 dans =0,968 {in}^ 2}\). Maintenant, vérifier si la section se comporte comme une tension contrôlée.
- \({a = frac{A_sfois f_y}{0.85\fois f'cfois b} = frac{0.968 {in}^2fois 60 KSI}{0.85\fois 4 ksifois 18 in }= 0.95 in}\)
- \({c = frac{a}{\bêta_1}= frac{0.95 in}{0.85} = 1.12 in }\)
- \({\varepsilon_t = (\frac{0.003}{c})\fois {(d – c)} = (\frac{0.003}{1.12 in})\fois {(17in – 1.12 in)} = 0.0425 > 0.005 }\) D'accord!, c'est une section à tension contrôlée!.
Calcul de la résistance à la flexion pour moment positif, \({M_{u,position} = 32.50 {kip}{pi}}\)
- Section présumée à tension contrôlée. \({\phi_f = 0.9}\)
- Largeur du faisceau, \({b=18 po}\)
- Zone de renfort en acier, \({A_s = frac{M_u}{\phi_ffois 0,9dfois fy}= frac{32.50 kip-ft times 12 en -ft }{0.9\fois 0.9(17 in )\fois 60 KSI}=0,472 {in}^ 2}\)
- \({\rho_{min} = 0.003162}\). Zone d'armature minimale en acier, \({UNE_{s,min}=rho_{min}\fois bfois d = 0.003162 \fois 18 en temps 17 dans =0,968 {in}^ 2}\). Maintenant, vérifier si la section se comporte comme une tension contrôlée.
- \({a = frac{A_sfois f_y}{0.85\fois f'cfois b} = frac{0.968 {in}^2fois 60 KSI}{0.85\fois 4 ksifois 18 in }= 0.95 in}\)
- \({c = frac{a}{\bêta_1}= frac{0.95 in}{0.85} = 1.12 in }\)
- \({\varepsilon_t = (\frac{0.003}{c})\fois {(d – c)} = (\frac{0.003}{1.12 in})\fois {(17in – 1.12 in)} = 0.0425 > 0.005 }\) D'accord!, c'est une section à tension contrôlée!.
Ensuite, nous pouvons voir que pour les deux moments, négatif et positif, le résultat est d'attribuer une armature de flexion minimale. La surface de barres d'armature en acier requise est égale à \(0.968 {in}^2).
Tutoriels associés
Si vous êtes nouveau chez SkyCiv, Inscrivez-vous et testez le logiciel vous-même!


