Aperçu
EN 1993-1-1: Conception de structures en acier (Eurocode 3) présente les lignes directrices de conception des éléments de construction en acier destinés à être utilisés dans les bâtiments utilisant la méthode de l'état limite. La conception à l'état limite implique de comparer les charges de conception pondérées avec des sections et des capacités réduites.. Ces facteurs sont destinés à tenir compte de la variabilité des conditions de chargement et des propriétés des matériaux.. Pour l’état limite ultime (ULS) concevoir pour être satisfait, la relation suivante doit être vraie:
\(ULS \;Facteur * Charge ≤ Réduction \;Facteur * Capacité)
Ce guide de conception décrit la procédure de conception d'un élément de construction en acier conformément à la norme EN 1993-1-1 en utilisant le EN 1993-1-1 Conception d'élément en acier module.
Regardez notre Eurocode 3 Démo de conception en acier
Contenu
Propriétés matérielles
Fabrication
EN 1993-1-1 fournit des conseils de conception pour quatre types de fabrication de structures en acier:
- Profilés laminés à chaud: Les sections laminées à chaud sont fabriquées en chauffant et en laminant des billettes d'acier dans un broyeur pour obtenir la forme requise.. Les exemples incluent les sections I UB/UC/UBP, Sections en T, Canaux et sections d'angle.
- Sections soudées: Soudé (ou fabriqué) les sections sont constituées de plusieurs plaques plates laminées à chaud soudées ensemble longitudinalement pour former une forme en acier. Les sections fabriquées sur mesure sont généralement soudées.
- Sections finies à chaud: Les sections finies à chaud sont produites en chauffant l'acier au-delà de sa température de recristallisation avant le laminage pour améliorer la résistance du produit final.. Ces profilés sont presque toujours des profilés creux structurels (RHS/SHS/CHS).
- Sections formées à froid: Les sections formées à froid sont fabriquées en pressant des billettes d'acier dans un broyeur à température ambiante.. Le formage à froid peut être utilisé pour produire des sections creuses structurelles et des sections ouvertes plus minces.. Note EN 1993-1-1 fournit uniquement des conseils pour les sections creuses formées à froid.
Nuance d'acier
L'Europe et le Royaume-Uni disposent de nombreuses qualités d'acier (forces) pouvant être utilisé pour la conception conformément à la norme EN 1993-1-1. Il existe plusieurs normes européennes de matériaux pour différents types de fabrication d'acier.:
- EN 10025: Produits laminés à chaud.
- EN 100210: Profilés creux structurels finis à chaud.
- EN 10219: Profilés creux structurels soudés formés à froid.
Profilés laminés à chaud (EN 10025)
Les disponibilités de nuances courantes et les limites d'élasticité indicatives pour les formes en acier laminées à chaud sont décrites ci-dessous.:
Limite d'élasticité minimale (MPa) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| Noter | ≤16mm | 16-40mm | 40-63mm | 63-80mm | 80-100mm | 100-150mm | 150-200mm | 200-250mm | 250-400mm |
| S 235 | 235 | 225 | 215 | 215 | 215 | 195 | 185 | 175 | 165 |
| S 275 | 275 | 265 | 255 | 245 | 235 | 225 | 215 | 205 | 195 |
| S 355 | 355 | 345 | 335 | 325 | 315 | 295 | 285 | 275 | 265 |
| S 460 | 460 | 440 | 420 | 400 | 390 | 390 | – | – | – |
Résistance à la traction minimale (MPa) |
||||||
|---|---|---|---|---|---|---|
| Noter | ≤3mm | 3-100mm | 100-150mm | 150-250mm | 250-400mm | |
| S 235 | 360 | 350 | 350 | 340 | 330 | |
| S 275 | 430 | 410 | 400 | 380 | 380 | |
| S 355 | 510 | 470 | 450 | 450 | 450 | |
| S 460 | – | 550 | 530 | – | – | |
Sections creuses structurelles finies à chaud (EN 100210)
Les disponibilités de qualités courantes et les limites d'élasticité indicatives pour les sections creuses structurelles finies à chaud sont décrites ci-dessous.:
Limite d'élasticité minimale (MPa) |
||||||
|---|---|---|---|---|---|---|
| Noter | ≤16mm | 16-40mm | 40-63mm | 63-80mm | 80-100mm | 100-120mm |
| S 235 H | 235 | 225 | 215 | 215 | 215 | 195 |
| S 275 H | 275 | 265 | 255 | 245 | 235 | 225 |
| S 355 H | 355 | 345 | 335 | 325 | 315 | 295 |
Résistance à la traction minimale (MPa) |
|||
|---|---|---|---|
| Noter | ≤3mm | 3-100mm | 100-120mm |
| S 235 H | 360 | 360 | 350 |
| S 275 H | 430 | 410 | 400 |
| S 355 H | 510 | 470 | 450 |
Rendement & Utilisez l'outil stylo pour ajouter rapidement des nœuds et des membres
La limite d'élasticité d'un matériau est la limite de contrainte au-delà de laquelle une déformation plastique se produira.. La résistance à la traction est la contrainte maximale qu'un matériau peut supporter avant de se rompre. / se brise. La limite d'élasticité et la résistance à la traction des sections en acier dépendent de la qualité et de l'épaisseur de l'acier.. Généralement, la résistance augmente avec la qualité de l'acier mais diminue avec l'augmentation de l'épaisseur de l'acier..
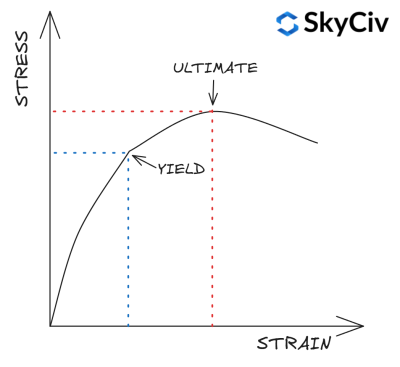
EN 1993-1-1 Le tableau 3.1 fournit une approche simplifiée pour calculer la limite d'élasticité et la résistance à la traction d'une section en fonction de sa qualité et de son épaisseur. Un calcul plus détaillé de la résistance du matériau peut être effectué en se référant à la norme de matériau pertinente.. Le SkyCiv FR 1993-1-1 Le module de conception des éléments en acier ne pas utiliser cette simplification et se référer aux normes de matériaux pertinentes pour le calcul de la résistance des matériaux.
Sélection d'une section dans SkyCiv FR 1993-1-1 Conception d'élément en acier
Le SkyCiv EN 1993-1-1 Conception d'élément en acier l'outil permet aux utilisateurs de sélectionner une section en acier standard dans la base de données SkyCiv ou de concevoir une section entièrement personnalisée. Le programme calcule automatiquement les valeurs de limite d'élasticité pour la semelle et l'âme de la section en fonction de la nuance d'acier sélectionnée.. Les utilisateurs peuvent également adopter une nuance d'acier personnalisée et saisir manuellement les propriétés des matériaux si nécessaire..
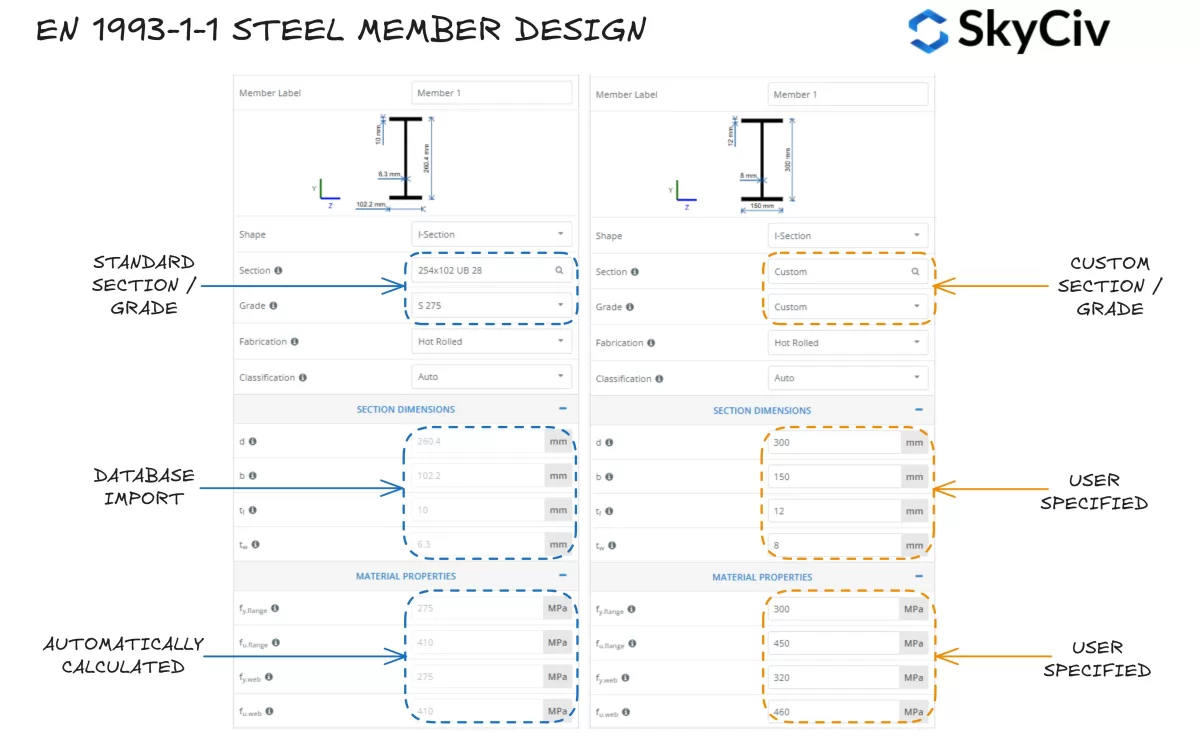
Classement des sections
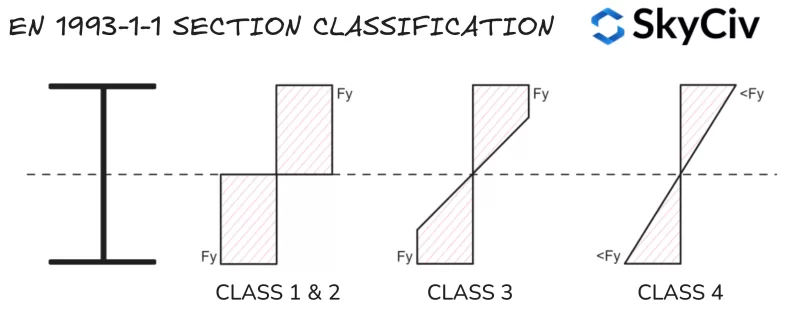
La classification des sections est un système utilisé par EN 1993-1-1 identifier la susceptibilité d'une section au flambement local avant d'atteindre sa pleine capacité plastique. Les grandes formes minces sont généralement plus sensibles au flambement local que les petites., formes trapues. Le SkyCiv EN 1993-1-1 Conception d'élément en acier l'outil calcule automatiquement la classification des sections en acier standard et personnalisées en fonction des conditions de chargement appliquées. Eurocode 3 comporte quatre catégories de classification de section:
- Classe 1: Sections pouvant former une charnière plastique et développer leur moment plastique/résistance axiale, ce qui signifie que la section entière peut atteindre sa limite d'élasticité sous flexion et/ou compression. Classe 1 les sections ont également une capacité de rotation élevée. Les propriétés des sections en plastique sont utilisées dans les calculs de capacité.
- Classe 2: Sections ayant la capacité de former une charnière en plastique mais ayant une capacité de rotation limitée. Eurocode 3 traite la classe 1 et classe 2 sections de la même manière pour presque tous les calculs de capacité.
- Classe 3: Sections pouvant atteindre la limite d'élasticité dans leur fibre à compression extrême, mais se déforme localement avant que la résistance du moment plastique ne soit atteinte. Les propriétés de la section élastique sont utilisées dans les calculs de capacité.
- Classe 4: Un flambage local se produira avant que la limite d'élasticité ne soit atteinte dans une ou plusieurs parties de la section.. Les propriétés de section élastique réduite sont utilisées dans les calculs de capacité.
Remarque, Classe 4 les sections incluent une complexité supplémentaire dans le calcul des propriétés de section / résistance et ne sont pas couverts dans ce guide.
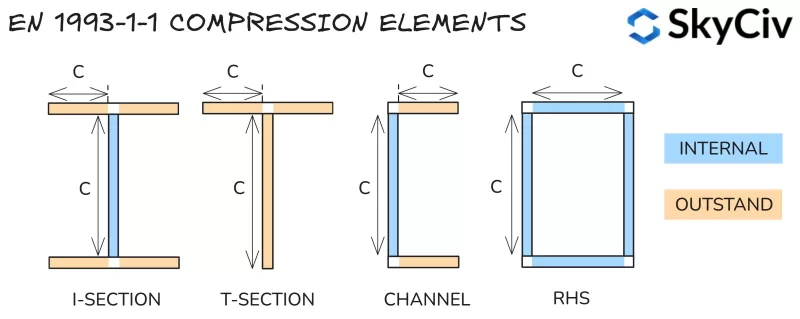
Éléments de compression
La classification des sections est déterminée en divisant une section en une série d'éléments de compression et en calculant leur élancement. (longueur claire par rapport à l'épaisseur). Les éléments sont classés comme suit ::
- Interne: Limité contre le flambage aux deux extrémités – e.g. toile d'une section en I.
- Exceptionnel: Uniquement retenu contre le flambage à une extrémité – e.g. bride d'une section en I.
Les valeurs d'élancement calculées sont comparées au tableau 5.2 en FR 1993-1-1 pour déterminer leur classe. Le classement de la section est considéré comme le classement le moins favorable de ses éléments de compression. Remarque, la classification des sections change en fonction des forces exercées sur la section (force axiale particulièrement variable). Les méthodes de classification de chaque type de chargement sont résumées ci-dessous.
Ratios de classification
Pièces soumises à la compression
Les éléments en compression pure sont classés en fonction de leur élancement uniquement en utilisant les limites indiquées ci-dessous..
| Classe | Pièces internes | Pièces exceptionnelles | |
| 1 | c / t ≤ 33ε | c / t ≤ 9ε | |
| 2 | c / t ≤ 38e | c / t ≤ 10ε | |
| 3 | c / t ≤ 42ε | c / t ≤ 14e | |
Où:
\(ε = sqrt{\frac{235}{f_y}}\)
Pièces sujettes à la flexion
Les éléments intérieurs en flexion pure sont classés en fonction de leur élancement dans les limites indiquées ci-dessous.
| Classe | Pièces internes | |
| 1 | c / t ≤ 72ε | |
| 2 | c / t ≤ 83e | |
| 3 | c / t ≤ 124e | |
Les éléments exceptionnels soumis à une flexion pure sont classés en fonction du rapport des contraintes de compression et de traction sous la valeur du moment de flexion, ce qui donne une contrainte de compression égale à la limite d'élasticité au niveau de la fibre extrême.. La méthode de calcul de ce ratio est détaillée dans la section ci-dessous.
Pièces soumises à la compression & Pliant
Les éléments soumis à une compression et une flexion combinées sont classés en fonction de leur capacité de compression. / répartition des contraintes de traction sous la charge de compression appliquée. Ce rapport est représenté par le symbole α pour la répartition des contraintes plastiques et le symbole ψ pour la répartition des contraintes élastiques..
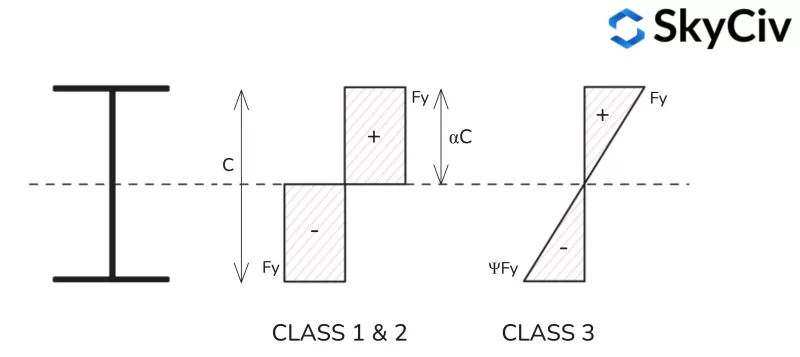
Répartition des contraintes plastiques
Formules de calcul du rapport de contrainte plastique (une) pour différents profils de forme sont fournis ci-dessous.
Répartition des contraintes plastiques en section I
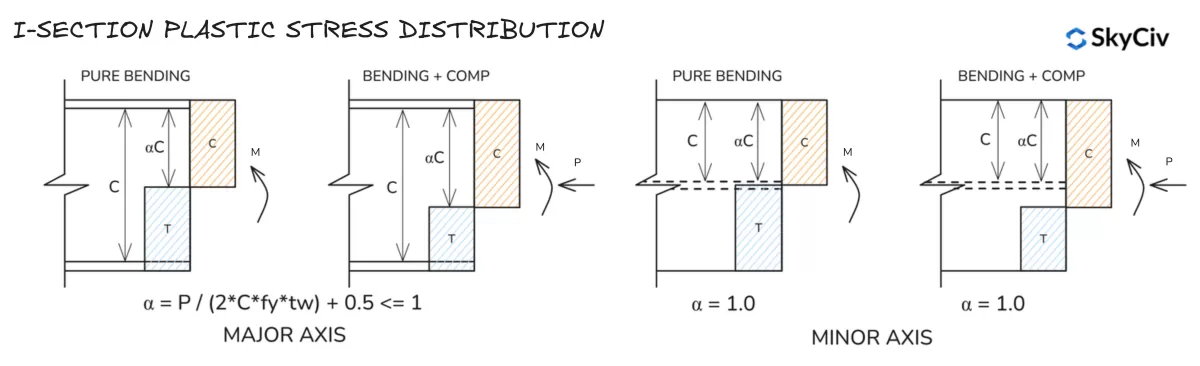
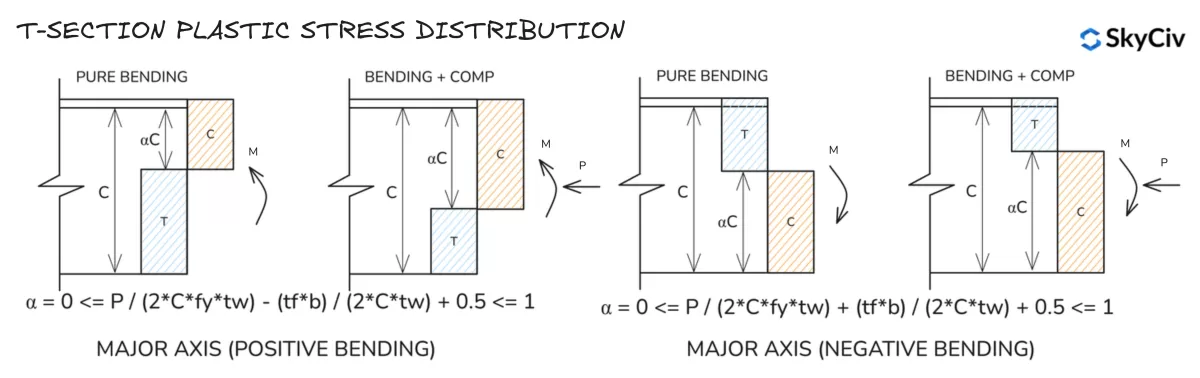
Répartition des contraintes plastiques en section en T
Notez que les distributions de contraintes des axes mineurs pour les sections en T sont similaires à celles d'une section en I..
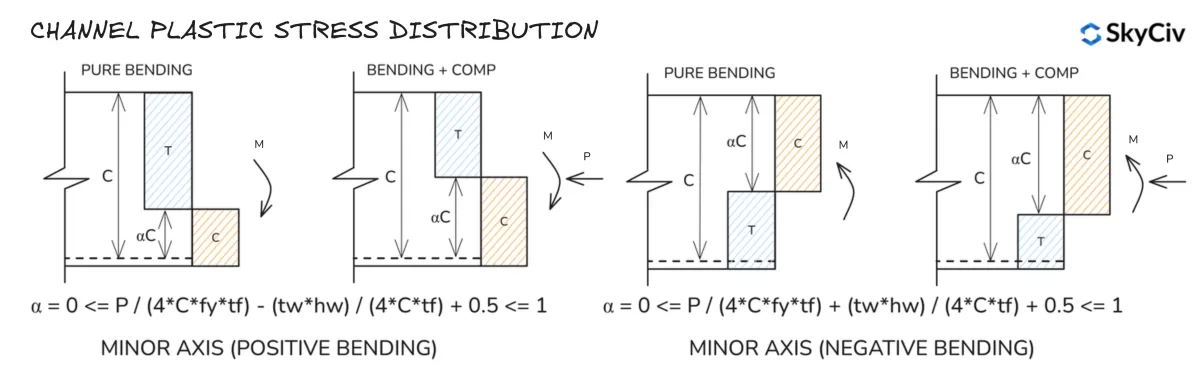
Répartition des contraintes de la section en plastique du canal
Notez que les distributions de contraintes sur les axes principaux des sections en T sont similaires à celles d'une section en I..
Répartition des contraintes plastiques RHS
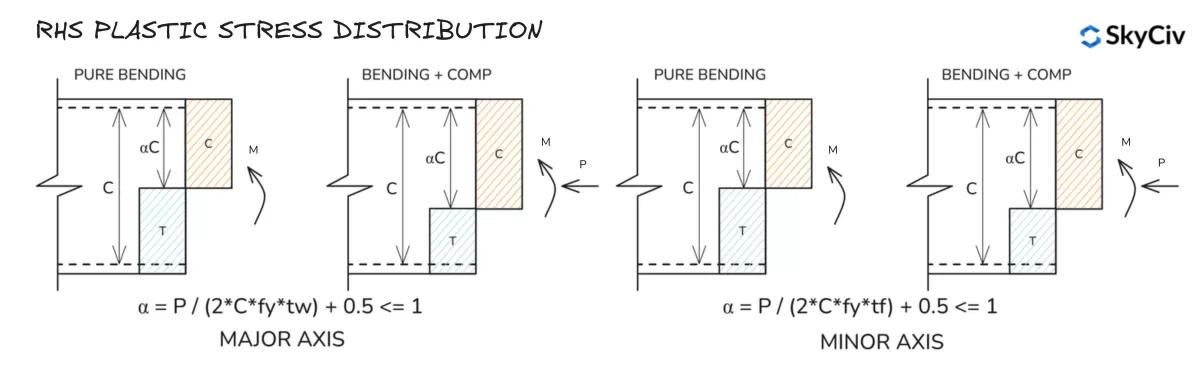
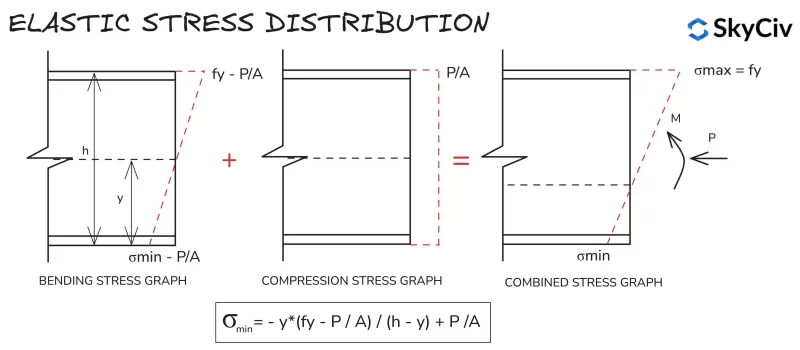
Répartition des contraintes élastiques
Les calculs de répartition des contraintes élastiques sont similaires pour toutes les sections et formes, en raison de la répartition linéaire des contraintes entre les fibres extrêmes. La formule de calcul de la contrainte minimale dans une section soumise à une compression et à une flexion appliquées est présentée ci-dessous..
Classification des sections dans SkyCiv FR 1993-1-1 Conception d'élément en acier
Ce logiciel SkyCiv UN 1993-1-1 Conception d'élément en acier L'outil détermine automatiquement la classification des sections des sections standard et personnalisées en fonction du chargement des entrées utilisateur.. Un exemple de sortie pour un Grade S 275, 430Le canal x100x64 avec 20 kN de charge de compression est détaillé ci-dessous.
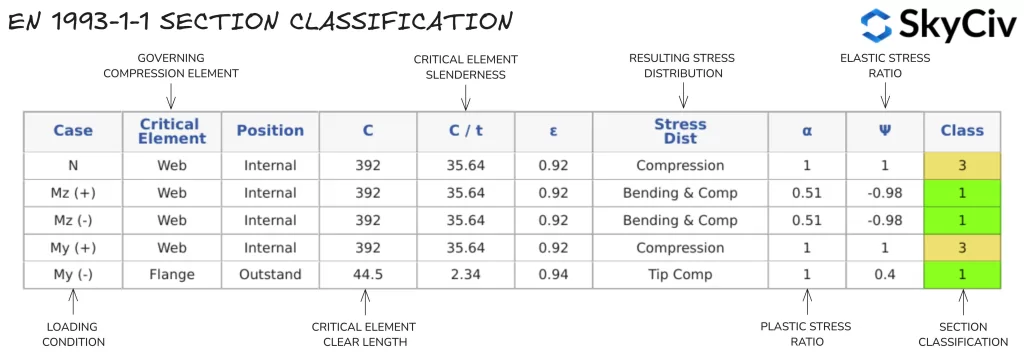
Une seule valeur de classification de section est utilisée pour tous les calculs basés sur la force axiale appliquée et la direction du moment de flexion appliqué.. Si un élément a un moment de flexion appliqué autour des deux axes, la classification la plus conservatrice de chaque direction est adoptée. Les utilisateurs peuvent également remplacer le calcul automatique de la classification des sections et spécifier une classification manuellement..
Remarque, Clause 5.4.1(3) spécifie que les sections symétriques (tels que les sections en T et les canaux) ne peuvent pas être conçus à l'aide de l'analyse plastique lorsqu'ils sont pliés autour de leur axe non symétrique. Par conséquent, les sections de cette nature se voient automatiquement attribuer une classe. 3.
Résistance des sections
Pliant
Résistance à la flexion des sections
La capacité de moment de flexion de la section est calculée à l'aide de la norme EN 1993-1-1 Clause 6.2.5.
\(M_{c,Rd} = W*f_y/γ_{M0}\)
Où W est le module de section plastique (WPL) pour la classe 1 & 2 les sections, ou le module de section élastique (Wil) pour la classe 3 les sections, FY est la limite d'élasticité du matériau et γ est le facteur de réduction partiel de sécurité.
Le module de section d'une forme est une propriété géométrique qui quantifie la résistance à la flexion d'une forme.. Le module de section plastique suppose que la section entière atteint sa limite d'élasticité en flexion. Le module de section plastique d'une section est calculé comme suit:
\(W_{PL} = A_{C} * y_{C} + UNE_{T} * y_{T} \)
Où unC et unT sont les zones de chaque côté de l’axe neutre plastique (ANP), Andyc / Yt sont la distance entre le PNA et le centre de gravité de ces zones. Remarque, l'emplacement du PNA est égal à l'emplacement du centre de gravité géométrique pour les formes symétriques mais sera ne pas égal à l'emplacement du centre de gravité géométrique pour les formes asymétriques.
Le module de section élastique assume toute la section (vers le bas) reste élastique en flexion, e.g. aucune partie de la section ne dépasse la limite d'élasticité (FY) du matériel. Le module de section élastique d'une section est calculé comme suit:
\(W_{il} = frac{I}{Y}\)
Où I est le deuxième moment de l'aire et y est le centre de gravité géométrique de la forme. Remarque pour une forme asymétrique, la valeur du module élastique utilisée dans la conception est la valeur la plus faible pour la flexion positive et négative autour de cet axe.
Calcul de la résistance à la flexion de section dans SkyCiv EN 1993-1-1 Conception d'élément en acier
Une fois que la classification de section pertinente a été calculée, le module calcule la capacité du moment de flexion de la section (Mc) autour de chaque axe principal. Les résultats pour le même canal 430x100x64 sont affichés dans l'exemple ci-dessous.

Tondre
Résistance au cisaillement des sections
La résistance au cisaillement est calculée selon EN 1993-1-1 Clause 6.2.6. Les calculs de capacité dépendent de la classification de section de l'élément en acier.. Capacité pour la classe 1 & 2 les sections sont calculées sur la base de la résistance au cisaillement plastique, alors qu'une résistance élastique au cisaillement est utilisée pour la classe 3 & 4 les sections.
La résistance au cisaillement plastique est calculée à l'aide de la formule ci-dessous:
\(V_{PL,Rd}=A_v * (f_y / \sqrt{3}) / c_{M0}\)
Où Av est l’aire de cisaillement de la section dans la direction de la force de cisaillement appliquée. Pour la plupart des sections, cette surface est équivalente à la surface de l'âme pour le cisaillement dans la direction de l'axe principal., et la surface des brides pour l'autre sens. Les formules de calcul de l'aire de cisaillement sont fournies dans EN 1993-1-1 Clause 6.2.6(3).
La résistance au cisaillement élastique est calculée à l'aide de la relation ci-dessous, ce qui garantit que la contrainte de cisaillement au point critique de la section transversale est inférieure à la limite d'élasticité.
\(t_{Ed}/(f_y / (\sqrt{3 * c_{M0}})) ≤ 1\)
La contrainte de cisaillement à ce point critique est calculée comme suit:
\(t_{Ed}=(V_{Ed} * S)/(I * t)\)
Où VEd est la force de cisaillement appliquée, S est le premier moment de l'aire, I est le moment de section et t est l'épaisseur à l'emplacement de contrainte critique.
La formule de contrainte de cisaillement élastique peut alors être arrangée pour représenter une valeur de résistance (en kN):
\(V_{il,Rd} = (I * t * \sqrt{3})/(S * f_y)\)
Flambage par cisaillement
Long, les âmes minces peuvent se déformer sous l'effet d'une force de cisaillement appliquée avant d'atteindre leur résistance élastique au cisaillement. Les âmes sont susceptibles de flamber par cisaillement si elles satisfont à la formule ci-dessous de l'EN 1993-1-1 Clause 6.2.6(6):
\(h / t > 72 * o/n \)
Où η est un facteur généralement pris comme 1.0. Les âmes sensibles au flambage par cisaillement doivent être vérifiées conformément à la section 5 de la norme EN 1993-1-5. Remarque, capacité de cisaillement selon EN 1993-1-5 n'est pas couvert dans le SkyCiv EN 1993-1-1 outil, mais un avertissement sera affiché si une section est susceptible de flamber par cisaillement.
Impact de la force de cisaillement sur la flexion & Résistance à la compression
Une force de cisaillement appliquée élevée peut avoir un impact négatif sur le moment et la résistance axiale d'une section.. En FR 1993-1-1, cet impact est capturé en réduisant la limite d'élasticité de la section par rapport à l'ampleur du cisaillement appliqué (se référer à la clause 6.2.8 & 6.2.10). Lorsque l'effort tranchant de section est de moins de la moitié de sa résistance au cisaillement plastique dans cette direction, cet impact peut être négligé. Si le cisaillement appliqué est supérieur à cette valeur, la limite d'élasticité réduite est calculée comme suit:
\(F_{Y,Rd} = (1 -ρ) * f_y \)
Où:
\(ρ = (2 * V_{Ed} / V_{PL,Rd} – 1)^2)
Ce logiciel SkyCiv UN 1993-1-1 Conception d'élément en acier le module calcule automatiquement toute réduction de la limite d'élasticité due à une force de cisaillement appliquée élevée et utilise cette valeur réduite dans les calculs de résistance à la flexion et à la compression des sections. Remarque, cette réduction ne s'applique que pour la résistance de section d'un élément, pas la résistance au flambage.
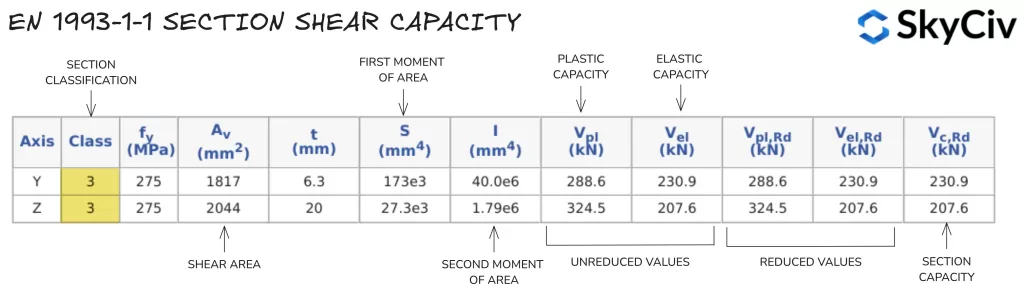
Calcul de la résistance au cisaillement dans SkyCiv EN 1993-1-1 Conception d'élément en acier
Ce logiciel SkyCiv UN 1993-1-1 Conception d'élément en acier l'outil calcule la capacité de cisaillement d'une section dans les deux directions de l'axe principal. Résultats des calculs de résistance au cisaillement pour un 254×102 UB 28 sont détaillés ci-dessous.
Compression
Résistance à la compression des sections
EN 1993-1-1 Clause 6.2.4 calcule la capacité de compression (Nc) d'une classe chargée de manière concentrique 1,2 ou 3 section comme suit:
\(N_{c,Rd} = A*f_y / c_{M0}\)
Où A est l’aire brute de la section transversale et fY est la limite d'élasticité de la section.
Calcul de la résistance à la compression de section dans SkyCiv EN 1993-1-1 Conception d'élément en acier
Ce logiciel SkyCiv Un 1993-1-1 Conception d'élément en acier l'outil calcule la résistance à la compression de la section (Nc,Rd) pour les sections européennes standard et les sections personnalisées définies par l'utilisateur. Résultats des calculs de résistance à la compression de section pour un 254×102 UB 28 sont détaillés ci-dessous.

Tension
Résistance à la traction des sections
EN 1993-1-1 Clause 6.2.3 calcule la capacité d'un élément de tension (NT) être la moindre entre la résistance à la tension plastique et la résistance à la tension ultime:
\(N_{t,Rd} = min(A*f_{Y}/c_{M0} \; ,\; 0.9*UNE_{n}*f_u /γ_{afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués})\)
Où A est la superficie brute de la section, An est l'aire nette de la section transversale (surface brute hors pénétrations/trous), FY est le limite d'élasticité de la rubrique, Fu est le traction (ultime) force de la section.
Calcul de la résistance à la tension dans SkyCiv FR 1993-1-1 Conception d'élément en acier
Ce logiciel SkyCiv UN 1993-1-1 Conception d'élément en acier le module suppose qu'aucun trou significatif n'est présent dans la section, donc An est pris égal à A. Résultats des calculs de résistance en traction de section pour un 254×102 UB 28 sont détaillés ci-dessous.

Pliant & Force axiale
Lorsqu'une section a appliqué une tension axiale ou une force de compression, l'effet de cette force sur la résistance du moment de flexion de la section doit être pris en compte. La méthode d'évaluation de cet effet décrite dans l'EN 1993-1-1 Clause 6.2.9 varie selon la classe 1 & 2 et classe 3 les sections.
Classe 1 & 2 Sections
La force de flexion et la force axiale combinées sont évaluées pour les sections en plastique en réduisant la résistance du moment plastique dans chaque direction d'une quantité proportionnelle à la force axiale.. Ce moment résistant réduit est désigné par le symbole MN,Rd. Calcul de MN,Rd varie en fonction de la forme de la section et est décrit dans EN 1993-1-1 Clause 6.2.9.1. Une fois le moment résistant réduit calculé, le critère suivant est utilisé pour évaluer la résistance combinée à la flexion et à la résistance axiale:
\( (M_{Y,Ed} / M_{Le,Rd})^un + (M_{z,Ed} / M_{Nouvelle-Zélande,Rd})^ b ≤ 1\)
Où α et β sont des constantes qui varient avec la forme de la section – Se référer à FR 1993-1-1 Clause 6.2.9.1.
Classe 3 Sections
La flexion combinée et la force axiale dans les sections élastiques sont plutôt évaluées à l'aide d'une formule générale de contrainte élastique détaillée ci-dessous.:
\( N_{Ed} / N_{c,Rd} + M_{z,Ed} / M_{cz,Rd} + M_{Y,Ed} / M_{cy,Rd} ≤ 1\)
Notez que toute réduction de la limite d'élasticité requise en raison de la force de cisaillement appliquée doit être utilisée dans le calcul des valeurs de résistance de section dans les formules ci-dessus..
Résistance au flambage
Pliant
Résistance au déversement par torsion latérale
Long, les éléments en acier non retenus peuvent se rompre en cas de déversement avant d'avoir atteint leur moment de résistance de section. Le déversement par torsion latérale se produit lorsque la section tourne de son grand axe vers son petit axe., ce qui signifie que la résistance du moment dans la direction de la flexion appliquée est réduite. Des lignes directrices pour le calcul de la résistance au déversement par torsion des éléments sont fournies dans l'EN. 1993-1-1 Clause 6.3.2.
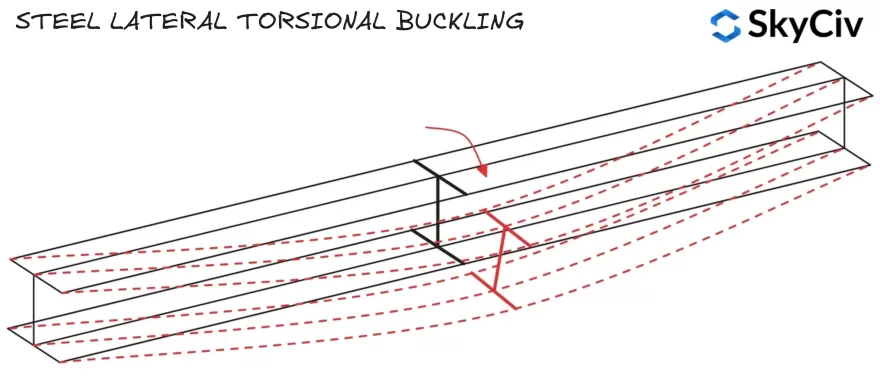
La résistance au déversement par torsion latérale est calculée à l'aide de la formule ci-dessous:
\(M_{b,Rd} = x_{LT}*W*f_y/ γ_{M1}\)
Où W est le module de section plastique (WPL) pour la classe 1 & 2 les sections, ou module de section élastique (Wil) pour la classe 3 les sections. hLT est un facteur de réduction du déversement, des indications pour le calcul de ce facteur sont fournies dans l'EN 1993-1-1 Clause 6.3.2.2 et 6.3.2.3.
Bride de compression
Les éléments échouent en cas de déversement par torsion lorsque la semelle comprimée tourne et se déplace latéralement.. Si la bride de compression d'un élément est suffisamment retenue, il ne sera pas sensible au déversement par torsion (Se référer à FR 1993-1-1 Clause 6.3.2.1(2)). Les emplacements des brides de compression pour les sections standard soumises à une charge verticale sont indiqués ci-dessous..
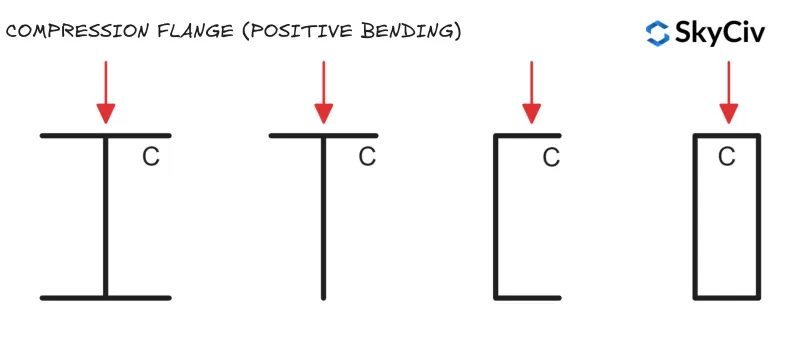
Sections creuses circulaires (CHS) et sections creuses carrées (SHS) ne sont pas sensibles au déversement par torsion, car ils ont un moment de résistance de section égale autour des deux axes (ce qui signifie que le déplacement latéral et la rotation n'affectent pas la résistance à la flexion de l'élément).
Facteur de réduction du flambement de la torsion latérale
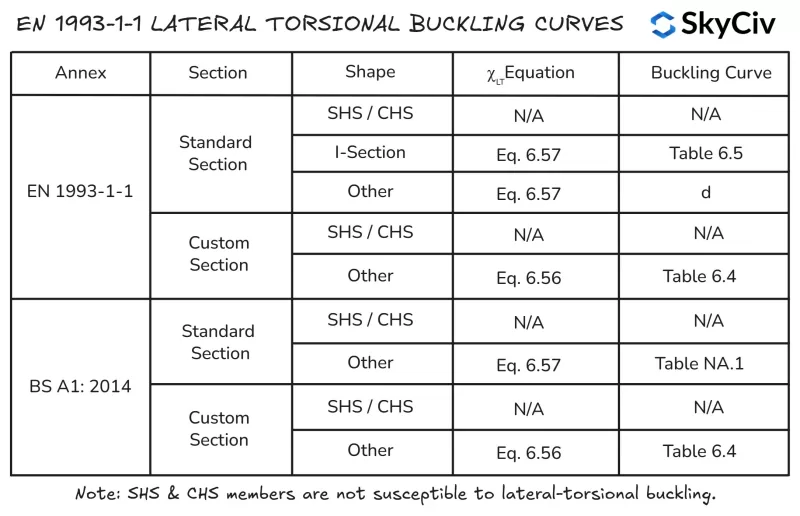
hLT est calculé dans EN 1993-1-1 en utilisant l'une ou l'autre section 6.3.2.2 (Cas général) ou section 6.3.2.3 (Sections roulées ou sections soudées équivalentes). Section 6.3.2.3 est applicable pour tous “nommée” sections et formes (y compris des sections creuses) et leurs équivalents soudés. Section 6.3.2.2 s'applique à toute section qui ne tombe pas dans la première catégorie, y compris des sections fabriquées et construites personnalisées.
Section 6.3.2.2 utilise l'équation 6.56 Pour le calcul de la réduction de la torsion latérale FACT0R χLT Alors que la section 6.3.2.3 utilise l'équation 6.57. Ce logiciel SkyCiv UN 1993-1-1 Conception d'élément en acier Le module suit la logique décrite ci-dessous pour l'application de l'équation 6.56 et 6.57.
Résistance au flambage par flexion des axes mineurs
La capacité de flexion d'un élément plié autour de son petit axe est égale à la résistance de section du petit axe autour de cet axe.. La capacité de section d'axe mineur est la capacité minimale qu'une section peut atteindre autour de n'importe quel axe., par conséquent, le membre ne peut pas tourner à partir de cet axe vers une orientation moins favorable.
Calcul de la résistance à la flexion des éléments en EN 1993-1-1 Conception d'élément en acier
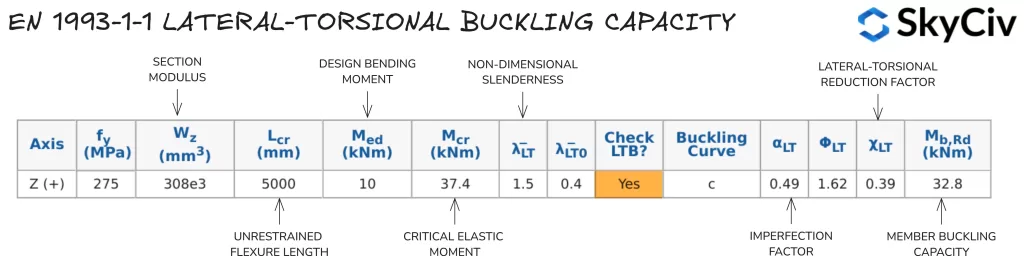
Ce logiciel SkyCiv UN 1993-1-1 Conception d'élément en acier l'outil calcule effectue des calculs de résistance à la torsion latérale conformément à la norme EN 1993-1-1 Clause 6.3.2.2 et clause 6.3.2.3, en fonction de la forme de la section et de l'Annexe Nationale appliquée. Les utilisateurs ont également la possibilité de spécifier un membre comme ayant “Retenue de torsion continue” qui ignorera automatiquement toutes les vérifications de déversement. Calculs de résistance au déversement par torsion pour un 254 de 5000 mm de long×102 UB 28 sont détaillés ci-dessous.
Compression
Résistance au flambement par flexion
La résistance au flambement par compression d'un élément est également affectée par sa longueur et sa rigidité latérale.. Effréné, les éléments plus longs sont susceptibles de se rompre en raison du flambement par flexion avant la section (squash) la capacité est atteinte. EN 1993-1-1 Clause 6.3.1.3 fournit des conseils sur le calcul de la résistance au flambement par flexion des éléments pour la classe 1, 2 & 3 des sections transversales:
\(N_{b,Rd} = x*A*f_y/ γ_{M1}\)
Où χ est un facteur de réduction pour le flambement par flexion. Des lignes directrices pour le calcul de ce facteur sont fournies dans EN 1993-1-1 Clause 6.3.1.3. Fla capacité lexurale doit être vérifiée autour des deux axes pour trouver la valeur déterminante pour le membre.
Calcul de la résistance au flambement par flexion en EN 1993-1-1 Conception d'élément en acier
Ce logiciel SkyCiv UN 1993-1-1 Conception d'élément en acier l'outil calcule la résistance au flambement par flexion autour des deux axes principaux en fonction des longueurs de retenue et des facteurs de longueur effective spécifiés par l'utilisateur. Résistance au flambage par flexion d'un 254×102 UB 28 avec une longueur libre de 6 000 mm et 5 000 mm dans les axes Z et Y (respectivement) sont détaillés ci-dessous.

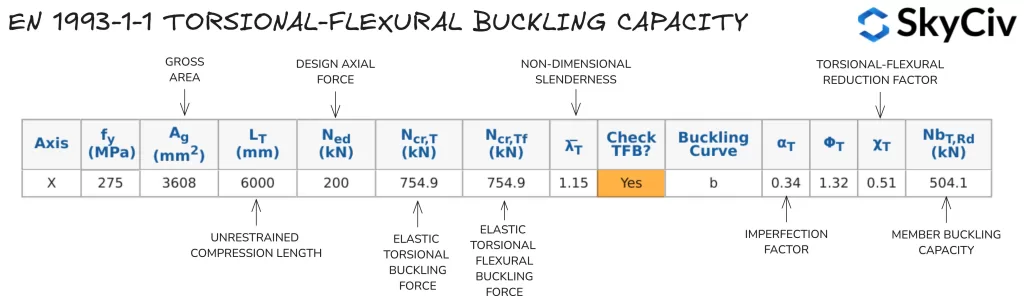
Résistance au flambage torsion-flexion
Les sections transversales ouvertes sont également sensibles au flambement par torsion et flexion., qui peut être inférieure à la résistance de la barre au flambement par flexion. Sections creuses circulaires (CHS) et sections creuses carrées (SHS) les éléments ne sont pas sensibles au flambement par torsion-flexion. EN 1993-1-1 Clause 6.3.1.4 fournit des conseils sur le calcul de la résistance au flambement par torsion et flexion des éléments:
\(N_{bT,Rd} = χ_T*A*f_y/ γ_{M1}\)
Où hLT est un facteur de réduction pour le flambement par torsion-flexion. Des lignes directrices pour le calcul de ce facteur sont fournies dans EN 1993-1-1 Clause 6.3.1.3. Fla capacité lexurale doit être vérifiée autour des deux axes pour trouver la valeur déterminante pour le membre.
Calcul de la résistance au flambement par torsion et flexion en EN 1993-1-1 Conception d'élément en acier
Ce logiciel SkyCiv UN 1993-1-1 Outil de conception d'éléments en acier calcule la résistance au flambement par torsion et flexion pour les sections ouvertes et fermées applicables conformément à la norme EN 1993-1-1 Clause 6.3.1.4 basé sur la longueur de retenue en compression dans l'axe principal, comme spécifié par l'utilisateur. Résistance au flambement torsion-flexion d'un 254×102 UB 28 avec une longueur libre de 6000 mm sont détaillés ci-dessous.
Logiciel de conception structurelle SkyCiv
SkyCiv propose une large gamme de logiciels d'analyse structurelle et de conception technique, y compris:
-
- Eurocode 3 Steel Design
- Eurocode 9 Conception en aluminium
- Eurocode 3 Conception des pannes
- Eurocode 3 Calculateur de groupe de boulons
- Eurocode 3 Calculateur de groupes de soudure
- Eurocode 2 Calculateur de longueur de développement
- Eurocode 2 Calculateur de longueur de tour
- Eurocode 5 Calculateur de conception en bois
- Eurocode 3 Calculateur de conception d'échafaudage
Développeur de logiciels | Ingénieur en structure
BEng (Civil), DipEng (Logiciel)



