频率分析的定义?
在设计建筑物时, 那里有两个 负载类型 考虑: 静态和动态. 对于第一个, 只需要计算结构对以位移和应力形式施加的永久载荷的直接响应. 这可以使用刚度或有限元方法来实现.
在动态分析的情况下, 由于时间相关的载荷,考虑结构响应的可能变化范围更具挑战性. 因此, 一些新工具或功能变得必不可少,必须包含在分析中. 所以, 频率分析, 振动力学的基本方法, 出现.
该方法获得由于施加的动态载荷引起的结构运动随时间的变化. 进一步来说, 这意味着使用结构系统振动的自然特性来计算内力, 位移, 稳定性问题, 等等.
有关该主题的更多信息, 我们建议阅读一篇 SkyCiv 文章,该文章简要说明了如何执行 动态频率分析 使用 SkyCiv结构分析软件.
为什么频率分析与设计相关?
衡量设计中频率分析重要性的最佳方法是观察一些因不良动态行为而失败的结构案例. 北美的一座著名桥梁是塔科马海峡, 在风引起的持续周期性振动后最终倒塌. 下图将显示坍塌前沿桥增加的位移, 主要集中在道路上:

图一. 塔科马海峡大桥的横向扭转振动

图二. 倒塌前桥梁位移增加.

图三. 灾难性的桥梁坍塌
在这个案例研究中, 没有进行适当的频率分析,并且结构设计没有充分考虑结构的自然频率.
单摆
频率分析研究结构在受到外部动态作用时发展的不同形式. 这就是为什么你会得到几个不同的 模式. 然后使用这些表格, 我们可以通过保证平衡所需的内力来确定结构的元素大小.
在深入研究频率分析的技术和数学考虑之前, 复习下一个简单的摆柱系统,如图 iv 所示.
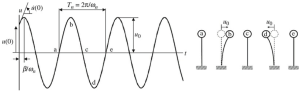
图四. 自由振动摆系统的动态响应
使用最后一张图片中所示的简单分析, 我们可以每次都定义摆柱顶部质量的运动. 本文的主要目标是涵盖两个典型案例的频率分析, 单自由度和多自由度.
单自由度
这种特殊情况对于动态分析来说是最简单的. 使用 D'Alembert 的平衡定律描述行为, 牛顿第二定律的扩展.
下图显示了 SDOF 系统的元素, 刚性 (ķ), 减震 (C), 和海量来源 (米) 对于惯性力. 施加在质量上的随时间变化的外力表示为 \({p(Ť)}\).
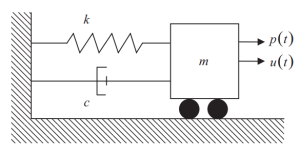
数字 1. 单自由度 (单自由度) 系统. (碗, 2017, 页 56)
所有元素都必须满足动态平衡条件:
\({米}{\点{ü}}+{C}{\点{ü}}+{ķ}{ü}={p(Ť)}\)
这是一个线性二阶微分方程, 它的解决方案有两个组成部分:
\({ü(Ť)}={ü}_{H}(Ť)+{ü}_{p}(Ť)\)
在哪里:
- \({ü(Ť)}\) 是绝对位移.
- \({ü}_{H}(Ť)\) 是齐次解, 通常涉及自由振动情况.
- \({ü}_{p}(Ť)\) 是根据施加的激励的特定解决方案.
我们将只关注描述振动行为和结构具有的最关键动态特性的均匀解.
让我们定义以下术语:
\({\钢底板设计欧洲规范{ñ}}={\sqrt(\压裂 {ķ}{米})}\) 角频率
\({\习}={\压裂{C}{{2}{米}{\omega_n}}}={\压裂{C}{{2}{\sqrt(\压裂 {ķ}{米})}}}\) 临界阻尼分数
当临界阻尼分数小于 1, 振动情况会欠阻尼; 那是, 在运动停止之前会有完整的循环.
解决方案具有以下一般形式
\({你_h}={e^{{-\习}{\钢底板设计欧洲规范{ñ}}{Ť}}}{[{一个}{cos}{\omega_d}{Ť}+{乙}{没有}{\omega_d}{Ť}]}\)
在哪里:
- A 和 B 是取决于运动初始条件的积分常数.
- \({\omega_d}={\omega_n}{\sqrt({{1}-{\习^2}})}\) 是阻尼角频率
一旦评估 A 和 B 常量, 无阻尼情况的一般解决方案是
\({你_h}={e^{{-\习}{\钢底板设计欧洲规范{ñ}}{Ť}}}{[{你_0}{cos}{\omega_d}{Ť}+{\压裂{{\点{你_0}}+{\习}{\omega_n}{你_0}}{\omega_d}}{没有}{\omega_d}{Ť}]}\)
在哪里:
- \({你_0}\) 是质量初始位移
- \(\点{你_0}\) 是质量初始速度
如果我们用一些初始条件值绘制解, 我们将得到下图.
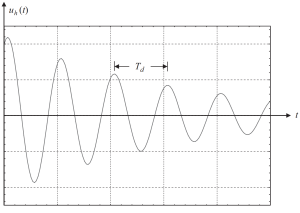
数字 2. 在亚临界阻尼情况下,位移导致解的均匀部分. (碗, 2017, 页 58)
在另一种情况下, 分析当临界阻尼分数的值为 1. \({\习}=1). 这种情况意味着具有完全阻尼的结构.
使用的方程是
\({你_h}={e^{{-\钢底板设计欧洲规范{ñ}}{Ť}}}{\{你_0+({\点{你_0}}+{\omega_n}{你_0}){Ť}}\}\)
他们的图表显示了不同的初始条件情况,如下图所示.
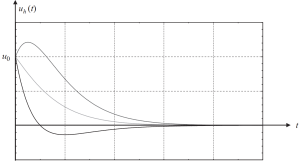
数字 3. 在临界阻尼情况下,位移导致解的均匀部分. (碗, 2017, 页 58)
响应参数
上一节帮助我们定义了 SDOF 系统中自由动态振动的解决方案. 两个主要参数是固有频率 \(\omega_n\) 这表明结构将如何自行振动, 和临界阻尼的分数 \(\习), 它定义了衰减振动的速度.
通常, 结构具有低阻尼,最大值为 \(\习)=10 %. 如果我们使用该值评估阻尼固有频率, 结果是 \({\omega_d}=0.995{\omega_n}\). 所以, 建议使用 \({\omega_d}{\厚约}{\omega_n}\).
我们可以在下表中总结动态属性.
| 角频率 (弧度/秒) | 固有频率 (赫兹) | 自然期 (s) | |
|---|---|---|---|
| 角频率 \({\omega_n}\) | \({\omega_n}\) | \(2{\pi}{f_n}\) | \(\压裂{2{\pi}}{T_n}\) |
| 固有频率 \({f_n}\) | \(\压裂{\omega_n}{2{\pi}}\) | \(f_n\) | \(\压裂{1}{T_n}\) |
| 自然期 \({T_n}\) | \(\压裂{2{\pi}}{\omega_n}\) | \(\压裂{1}{f_n}\) | \(T_n\) |
桌子 1. 角频率之间的关系, 自然频率, 和时期 (碗, 2017, 页 60)
多自由度
当结构中存在许多质量时, 我们必须定义多个坐标来随时描述这些质量的位置. 下图显示了一个特定且明显的示例, 由一个复杂的摆组成,其中需要不同的角度来确定每个运动时刻的位置.
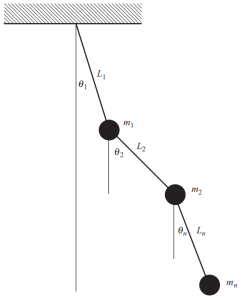
数字 4. 具有多个质量的摆. (碗, 2017, 页 53)
在这个部分, 我们分析结构’ 使用多自由度的属性频率分析扩展的一般动态响应.
在处理实际结构时必须了解建模过程. 下图描述了构建准备好应用频率分析来描述其动态响应的数学模型所需的步骤.
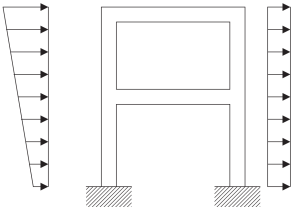
数字 5. 连续结构框架的物理模型. (碗, 2017, 页 23)
第一步涉及在梁和柱的每个水平交叉点集中质量. 每个节点都有三种可能的运动, 两个线性位移, 和一圈. 在分析中保持一致, 必须考虑质量和极惯性特性.
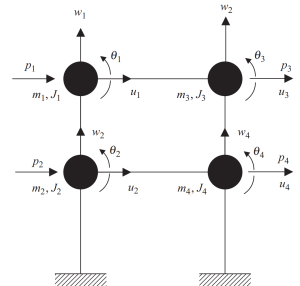
数字 6. 具有位移和旋转自由度的节点处的集中质量. 离散系统. (碗, 2017, 页 23)
静态冷凝法有助于降低分析的复杂性, 忽略旋转和平移惯性.
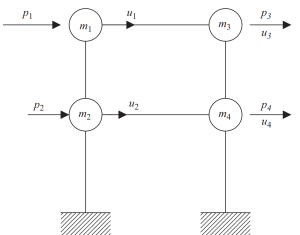
数字 7. 自由度静态压缩为仅水平位移. (碗, 2017, 页 23)
在最后一步, 我们可以仅将两个节点集中在这个框架示例的水平运动中.
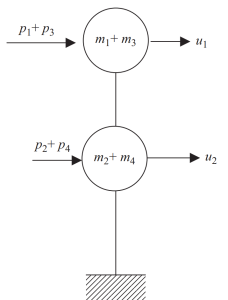
数字 8. 两节点最终静力凝结及水平位移自由度. (碗, 2017, 页 24)
正如我们在上一节中对 SDOF 系统所做的那样, 我们将开发多自由度运动方程的解.
运动方程写成矩阵形式为
\([m]\{\点{ü}\} + [C]\{\点{ü}\}+[ķ]\{你}={p(Ť)}\)
在哪里:
- \([m]\) 是质量矩阵
- \([C]\) 是库仑的阻尼矩阵
- \([ķ]\) 是个 刚度矩阵
我们必须研究自由振动解以获得响应参数. 系统没有阻尼和力, 仅评估初始条件.
\([m]\{\点{ü}\} +[ķ]\{你}={0}\)
类似于 SDOF 的第一种情况, 我们可以测试形式的正弦解.
\({ü(Ť)}={\φ}{({一个}{cos}{\欧米茄}{Ť}+{b}{没有}{\欧米茄}{Ť})}\)
\({\点{ü}{(Ť)}}={-{\欧米茄}^ 2}{\φ}{({一个}{cos}{\欧米茄}{Ť}+{b}{没有}{\欧米茄}{Ť})}\)
其中向量 \(\φ) 是一个不依赖于时间的形状向量. 系数 “一个” 和 “b” 是评估初始条件时获得的常数.
将测试解的两个表达式代入运动方程后, 我们得到线性特征值-特征向量问题:
\([ķ]{\φ}={{\欧米茄}^ 2}[m]{\φ}\)
在哪里:
- \({{\欧米茄}^ 2}\) 是特征值的集合
- \({\φ}\) 是特征向量集
最新图中框架示例的这个经典问题的解决方案显示了质量将如何振动. 这意味着每个质量将根据特征向量的值在水平方向上移动.
看下图这个行为.
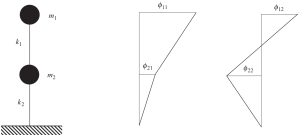
图 9. 显示两个特征向量结果的频率分析. (碗, 2017, 页 135)
SkyCiv结构3D
对您的结构执行频率分析 SkyCiv结构3D. 立即注册以开始使用!
参考资料:
- 爱德华多考塞尔, (2017). “高级结构动力学” 1st版, 剑桥大学出版社


