目录
支持的类型及其反应
在这篇文章中, 我们讨论反作用力公式以及如何找到支撑反作用力. 第一, 了解不同类型的支撑以及它们在分析模型中产生的反应也很重要. 以下是不同支持类型及其反应的简短备忘单:
| 支持类型 | 翻译 | 回转 | 笔记 |
|---|---|---|---|
固定支持 |
各个方向固定 X 中的反应,和,与 |
各个方向固定 X 中的反应,和,与 |
FFFFFF – 所有自由度的反应 |
水平滚轮支撑 |
固定在 Y 仅在 Y 方向发生反应 |
全方位释放 无旋转反应 |
射频FRRR – 反应仅在 Y 方向 |
固定或铰接支撑 |
固定在 X,和,与 X 中的反应,和,与 |
全方位释放 无旋转反应 |
FFFRRR – 所有翻译中的反应, 没有轮换 |
| 悬臂支撑 |
各个方向固定 X 中的反应,和,与 |
各个方向固定 X 中的反应,和,与 |
与固定相同 |
确定梁中支撑反应的分步指南:
确定梁中支撑反作用力的分步指南, 这通常是最简单的. 它涉及计算支撑处的反作用力 (在下面的示例中支持A和B) 由于作用在梁上的力. 您需要知道这一点才能进行并计算 弯矩图 (骨密度) 和 剪力图 (差价合约); 静力学和结构性大学课程的重要组成部分. SkyCiv提供了强大的功能 自由反应计算器 可以为任何光束建模并为您显示这些手的计算, 但这也是一个重要的概念.
视频教程: 确定支撑处的反应
解决此类问题时，我们首先要记住光束是静态的; 表示它没有动. 来自简单物理学, 这意味着y方向上的力之和等于零 (即. 向下总力等于向上总力). 要记住的第二个公式是，任何给定点的力矩之和等于零. 这是因为光束是静态的，因此不旋转.
确定支撑处的反应, 遵循以下简单步骤:
1. 矩之和 (ΣM= 0)
在此阶段，我们需要知道的是它们等于力乘以到一个点的距离 (即. 力x距点的距离). 考虑一个简单的例子，一个4m的梁在A处有销钉支撑，在B处有滚柱支撑。. 自由图如下所示，其中A和 和B和 是支撑的垂直反应: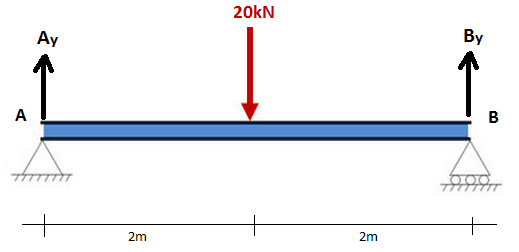
我们首先要考虑关于点 B 的矩的总和，让它等于零. 我们选择了点B来证明可以在光束的任一端完成此操作 (只要它受引脚支持). 然而, 您可以轻松地从A点开始工作. 所以, 现在我们求和B点的力矩，并求和 0:
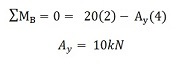
注意: 我们选择的符号约定是逆时针为正，顺时针为负. 这是最常见的符号约定，但取决于您. 您必须在整个问题中始终使用相同的符号约定. 从一开始就始终使用相同的符号约定. 现在我们有了第一个方程. 我们需要求解另一个方程式才能找到B和 (支撑B处的垂直反作用力).
2. 水平力之和 (ΣF和 = 0)
将y中的力求和 (垂直) 方向，使总和等于零. 记住要包括所有力，包括反作用力和法向载荷，例如点载荷. 因此，对于上面的示例，如果我们将y方向的力求和, 我们得到以下等式:
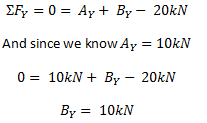
注意: 再次，我们坚持了一个标志惯例，那就是采取向上的力量 (我们的反应) 作为正面和向下的力量 (点负荷) 否定的. 请记住，符号约定取决于您，但是您必须在整个问题中始终使用相同的符号约定.
因此，我们有它, 我们使用了上面的两个方程 (力矩之和等于零，垂直力之和等于零) 计算得出载体A上的反应为 10 kN和载体B上的反应10kN. 这是有道理的，因为点载荷正好在梁的中间, 表示两个支撑件应具有相同的垂直力 (即. 它是对称的).
综上所述, 这是完整的 手工计算 由。。。生产 SkyCiv梁:
SkyCiv Beam软件
通过这篇文章, 您已经了解了支撑反作用力的概念以及如何计算支撑反作用力. SkyCiv 光束分析软件 允许用户轻松准确地分析梁结构. 你可以得到你的梁成员的分析, 包括反应, 剪力, 弯矩, 偏转, 压力, 和 不确定的光束 在几秒钟内.
如果你想先试一试, 自由光束计算器 是一个很好的开始方式, 或者今天就免费注册!
