静态确定性指南, 不确定性, 和不稳定

一旦结构完全建模并施加载荷, 是时候解决系统以找到来自分析阶段的所有结果: 反应, 内力 (剪力, 弯矩, 轴向力, 和扭转), 位移, 并强调. 有时事情并没有按预期进行，在解决问题时, 你可能会收到一条烦人的消息说 “解决失败! 检查您的结构设置, 因为模型可能不稳定”, 很可能你不知道模型到底出了什么问题. 本文解释了结构稳定性的概念以及非常相关的主题的静态确定性和不确定性, 它还提供了一些对不稳定模型进行故障排除的技巧.

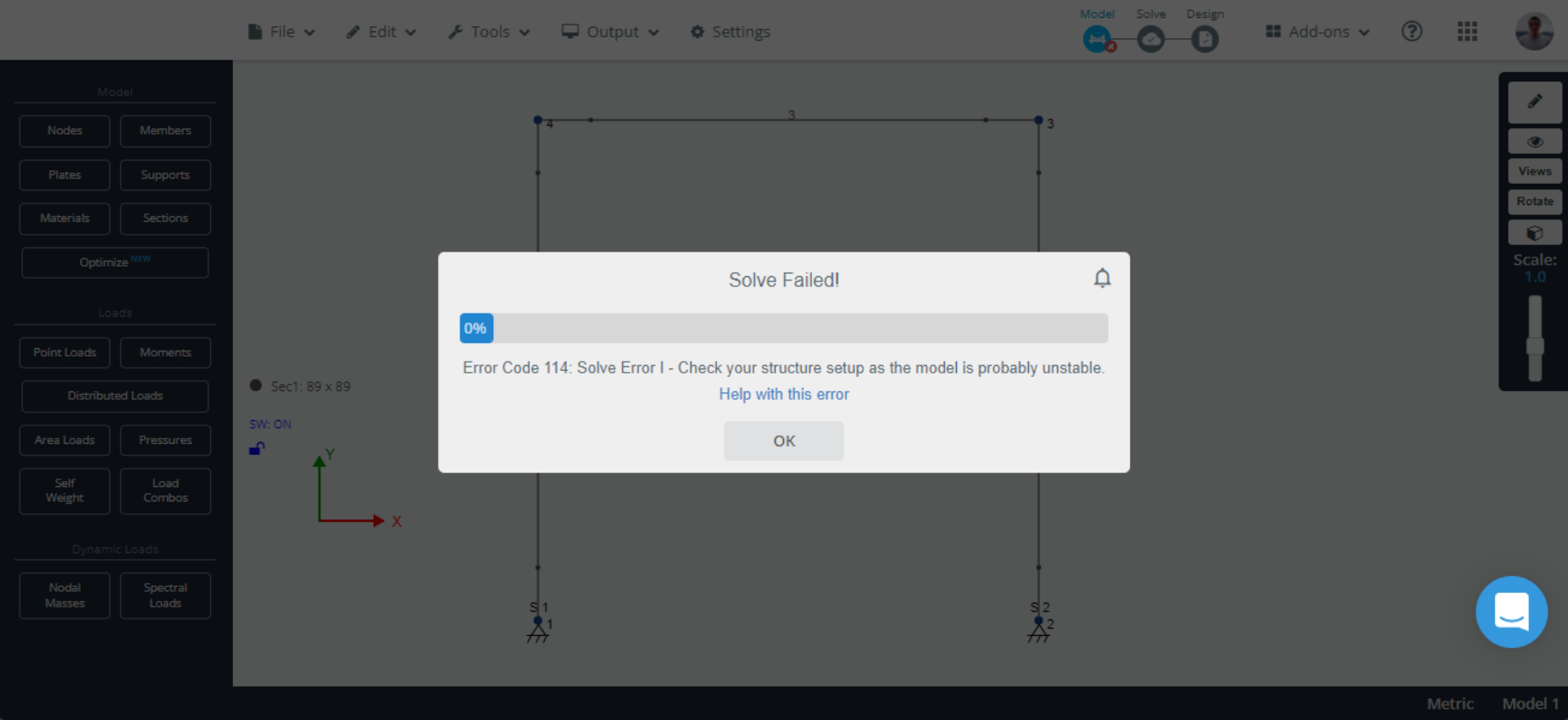
一般来说, 如果结构在移除支撑时保持其形状，则该结构被认为是内部稳定的. 反过来, 如果一个结构一旦与支撑分离，它就被认为是内部不稳定的, 结构无法保持其形状，可能会发生大位移甚至倒塌. 那说, 我们将仔细研究静态确定性公式, 适用于内部不稳定和稳定的结构. 静态确定性公式有助于将结构分类为外部不稳定, 静定, 或静态不确定的.

内部稳定结构的静力确定性

如果一个内部稳定结构的所有支撑反应都可以通过求解平衡方程来求解，那么它可以被认为是外部静定的. 对于平面内载荷下的平面结构, 结构平衡需要三个支持反应. 另外, 因为只有三个平衡方程可用, 最多可以找到三个反应, 所以应该正好有三个反应支持平面结构. 下图显示了一些外部静定平面结构的示例:

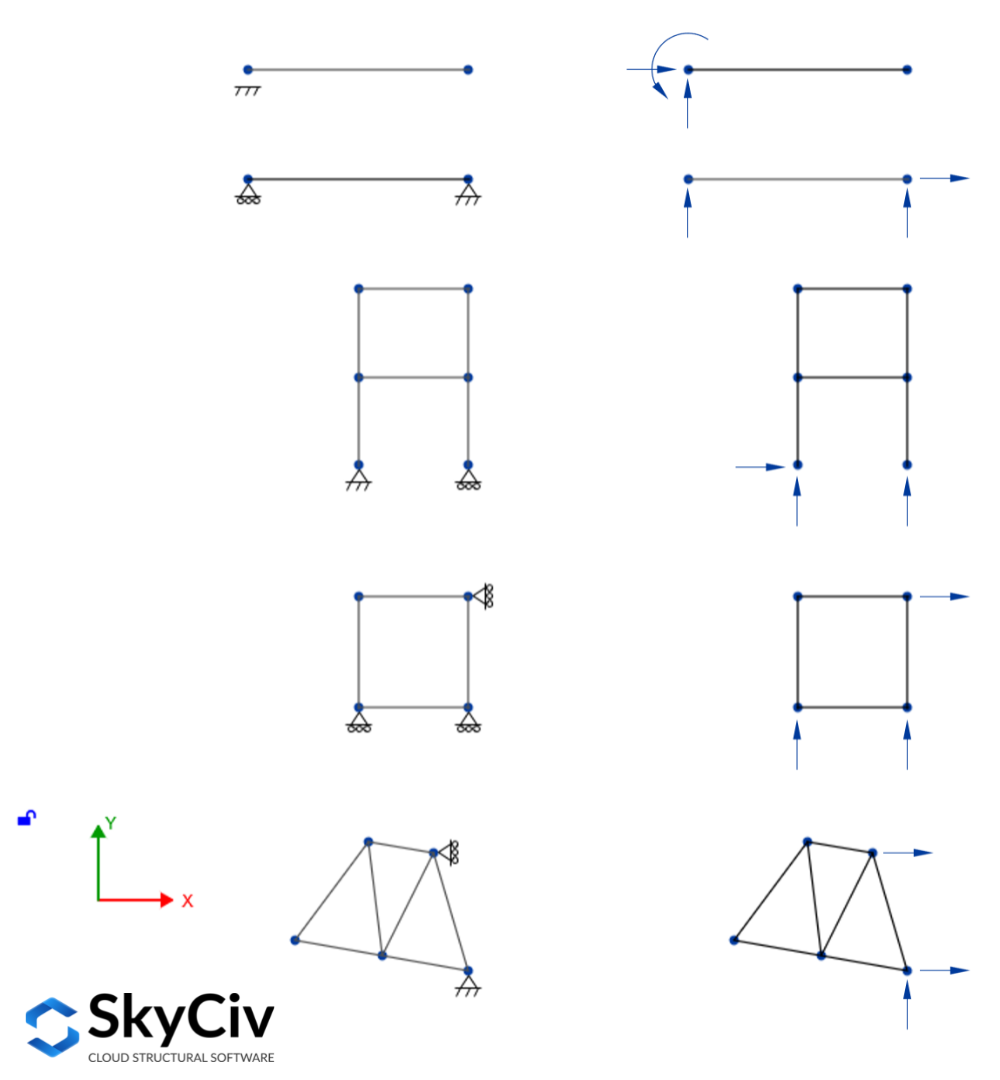
当超过三个反应支持结构时, 它被称为静态不确定的外部结构, 因为不可能使用三个平衡方程解决所有反应. 这些反应称为外部冗余，外部冗余的数量称为外部不确定度, 写成一个方程它看起来像这样:

\(i_e = r – 3\)

在哪里 \(r) 是支持结构的反应数量.

在结构由少于三个支撑反应支撑的情况下, 这些不足以阻止结构在其平面上移动, 由于该结构在一般载荷系统下不会保持平衡，因此称为外部静态不稳定. 根据反应次数 \(r), 可以确定静态确定性, 不确定性, 和内部稳定结构的不稳定性使用以下标准:

\( r 开始{案例} < 3, \; \文本{静态不稳定的外部结构} \\ = 3, \; \文本{静态确定的外部结构} \\ > 3, \; \文本{静不定外结构} \结束{案例}\)

值得一提的是，一旦满足最后两个条件, 不能保证结构会稳定. 这意味着即使结构由三个以上的反应支撑，如果支撑且布置不当，结构仍可能不稳定. 这称为几何外部不稳定性，主要由两个原因引起:

• 当所有反应’ 作用线是平行的，因为不会阻止结构在反应的垂直方向上位移
• 当所有反应’ 行动线在某一点是并发的，因为结构将被允许围绕并发点旋转

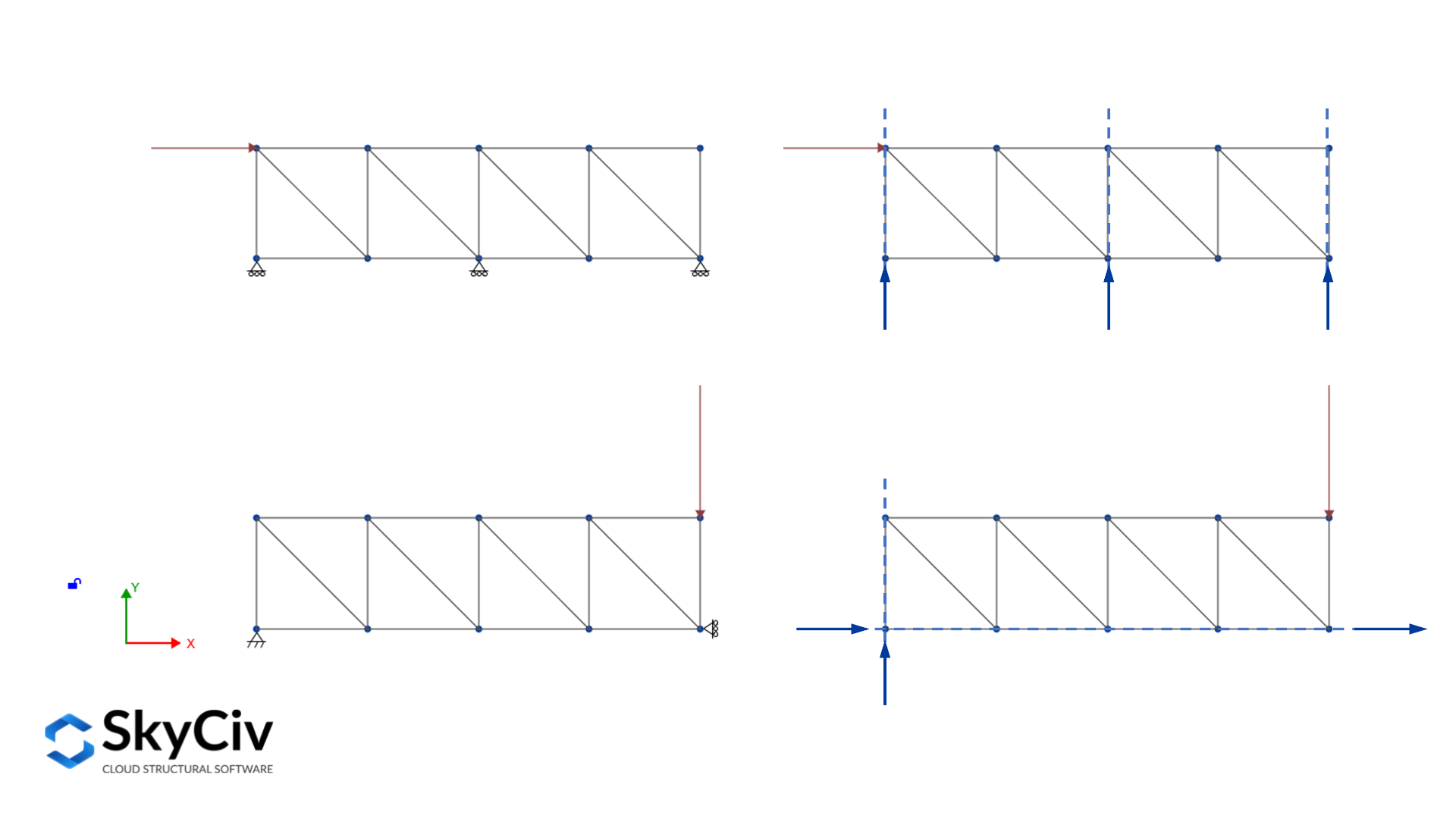
内部不稳定结构的静力测定

内部不稳定结构是指那些在与支撑分离时无法保持其原始形状的结构. 没有支撑, 结构的成员将发生相对于彼此的大位移. 定义静态确定性, 不确定性, 和这些结构的外部稳定性, 由于考虑到成员之间的特殊联系的附加条件方程起作用，方程发生了变化. 特殊连接是那些不传输时刻的连接, 剪力, 或轴向力.

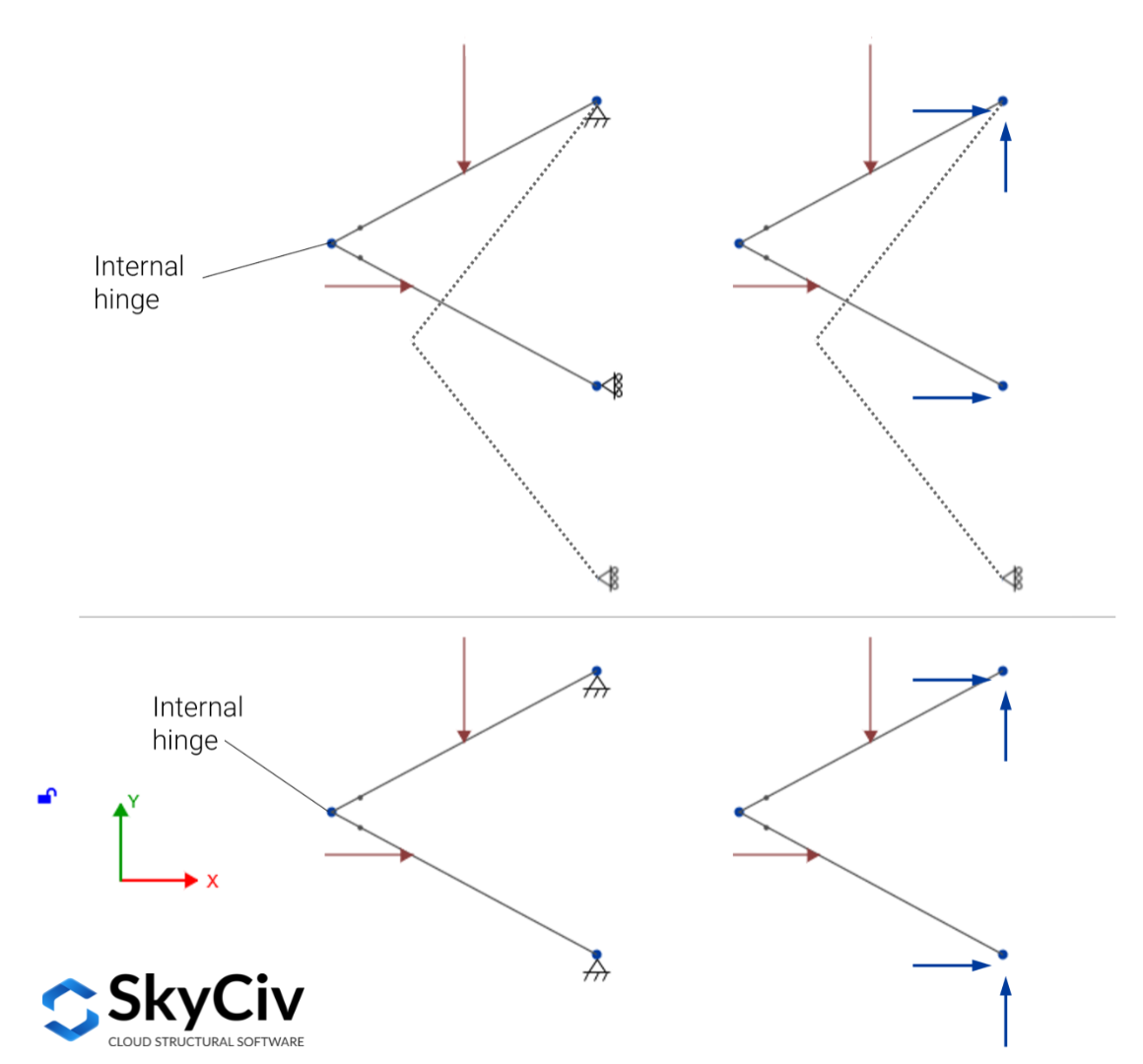
举个例子, 考虑下图中的结构 (顶部), 它得到三个反应的明确支持, 但由于构件之间存在铰链，这些不足以保证在施加的平面内力下的平衡, 它需要第四个非并行, 非同时反应以确保平衡 (底部).

一般来说, 对于内部不稳定的结构, 基于反应次数 \(r) 和条件方程 \(e_c), 可以确定静态确定性, 不确定性, 和内部稳定结构的不稳定性使用以下标准:

\( r 开始{案例} < 3 + e_c, \; \文本{静态不稳定的外部结构} \\ = 3 + e_c, \; \文本{静态确定的外部结构} \\ > 3 + e_c, \; \文本{静不定外结构} \结束{案例}\)

对于不确定的外部内部不稳定结构, 外部不确定性的程度可以表示为:

\(i_e = r – (3 + e_c)\)

包起来

对于内部稳定到外部稳定的平面结构, 意味着它在一般负载系统下保持平衡, 以下必须持有:

• 该结构由三个或更多反应支持
• 所有的反应不能并行也不能并发

对于内部不稳定到外部稳定的平面结构, 意味着它在一般负载系统下保持平衡, 以下必须持有:

• 支持结构的反应数大于等于条件方程数加三
• 所有的反应不能并行也不能并发

对 S3D 中的不稳定结构进行故障排除

当模型无法解决时，您可以尝试一些事情, 你得到了 “不稳定的结构” 错误信息:

• 选择所有成员并确保他们的成员最终固定为 “FFFFFF”, 并尝试运行模型. 如果某些成员需要在最终模型中具有不同的端部固定性, 开始一个一个地改变它并解决结构，看看哪个是导致不稳定的确切成员或一组成员.
• 选择所有成员并将其类型从正常更改为连续, 这将正确连接在交叉路口没有节点但打算连接的成员.
• 从分析中抑制所有电缆, 并尝试解决模型. 学习如何压制成员, 参考 本文.

参考资料

卡西马利, 阿斯拉姆. “3.4 静态确定性, 不确定性, 和不稳定。” 结构分析, 圣智学习, 2011.