如何检查列是否屈曲
在这个简短的教程中, 我们将介绍您需要了解的有关简单列的所有信息 屈曲 分析. 众所周知, 柱是承受高轴向压缩载荷的结构中的垂直构件. 承受压缩载荷的构件可能会遇到一种称为 “屈曲” 被描述为突然的侧向偏斜. 它不同于屈服, 但我们将在整个教程中对此进行解释.
欧拉屈曲理论
数学家莱昂哈德·欧拉(Leonhard Euler)研究了立柱的行为,并得出了使立柱弯曲所需的载荷的简单公式. 这称为 临界屈曲载荷:

这是一个相当简单的公式, 然而, 有一些重要的事情要注意. 首先, 成员的横截面有两个 惯性矩 价值观 (一世与 和我和), 所以你应该选择哪一个? 好吧,因为该公式与查找 批判的 屈曲负载,那么很明显,我们应该采取 最低 截面的惯性矩,因为这将产生最低的临界屈曲载荷 (即. 它将更快地弯曲). 其次, 而不是使用成员的实际长度, 大号, 我们改为使用 有效长度 列的, 吉隆坡. 那么这个K因子是什么,为什么有必要? 我们将在下一部分中讨论.
有效长度因子 (ķ)
欧拉是个聪明人,他很快就发现,立柱的长度需要根据两端的约束或支撑方式进行调整. 为此原因, 我们可以使用一个因素, 调整长度以得到KL的K. 有效长度因数的理论值和建议值 (ķ) 在下图中提供:
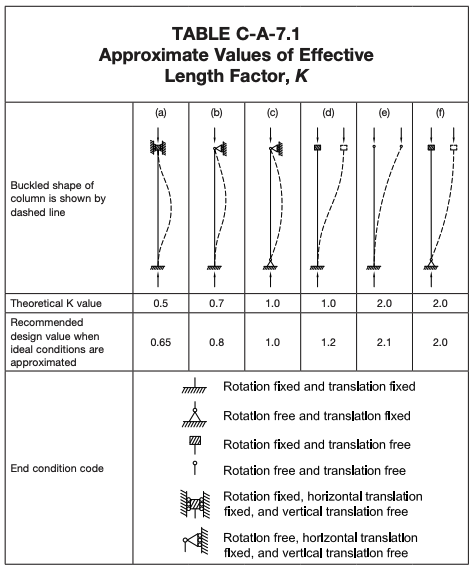
资源: AISC 360-22: 钢结构建筑规范
屈曲与屈服
屈曲和屈服是两种不同的失效形式. 当构件的应力超过材料的屈服强度时,就会发生屈服. 然而, 根据色谱柱的情况,屈服可能在屈服发生之前发生. 例如, 如果列’ 临界屈曲载荷为 20 kN,其面积仅为 1000 毫米2 那么它的临界屈曲应力将是:
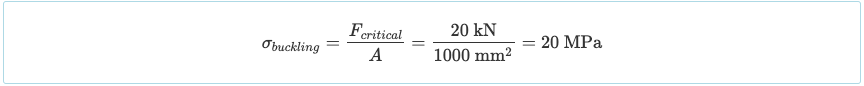
由于临界屈曲应力低于材料的屈服强度 (说 300 兆帕), 然后它会屈服才屈服.
列屈曲示例
让我们利用这些知识做一个例子:
假设我有一个100x20x3mm的RHS柱,它是由结构钢制成的 (E = 200 GPa). 如果长度为 3.0 米,固定在底部并固定在顶部, 在什么理论负荷下它将开始弯曲?
使用我们的 惯性矩免费计算器 我们可以看到RHS横截面的最低惯性矩为I = 45,172 毫米4. 对于结构钢E = 200 GPa = 200 千牛/毫米2. 使用上表,我们可以看到固定销柱的有效长度因子为K = 0.7 当然L = 3.0 m = 3000 毫米. 因此,我们可以使用欧拉的屈曲公式:

因此,一旦作用在构件上的轴向压缩力达到 20.22 kN以上,该成员理论上会弯曲!
我希望本教程可以帮助您了解有关如何简单计算列屈曲的更多信息. 看看我们的 免费的柱屈曲计算器, 列计算器 或立即注册以开始使用 SkyCiv 软件!


