钢结构分析与设计 受 AS 等标准管辖 4100:2020, 使用极限状态法来设计钢结构构件. 该方法涉及计算因子载荷和减少的容量,以考虑载荷条件和材料特性的变化. 对于最终极限状态 (超低硫) 设计要让人满意, 以下关系必须正确:
\(超低硫 \;因素 * 负载≤减少 \;因素 * 容量)
本文件概述了根据 AS 设计钢构件的程序 4100 使用 SkyCiv AS 4100:2020 钢构件设计 模块.
内容
材料特性
制造
在澳大利亚,钢结构制造有三种典型形式:
- 热轧型材: 钢坯 (块) 被加热, 通过磨机轧制成所需的形状, 然后冷却. 示例包括通用梁/柱, 平行法兰通道 (全氟辛烷磺酸) 和角截面.
- 冷弯型材: 钢坯在室温下被压制成所需的形状. 示例包括矩形空心截面 (RHS) 和圆形空心截面 (CHS).
- 预制型材: 将多块热轧平板焊接在一起形成型钢. 示例包括焊接梁/柱.
钢级
澳大利亚有多种钢种 (优势) 可用于符合AS的设计 4100:2020. 不同部分类型的等级可用性概述如下.
| 年级 | 世界银行 / 厕所 | UB / 加州大学 | 全氟辛烷磺酸 | 她 / UA | RHS / SHS | CHS |
|---|---|---|---|---|---|---|
| 250 | 不 | 不 | 不 | 不 | 不 | 是的 |
| 300 | 是的 | 是的 | 是的 | 是的 | 不 | 不 |
| 350 | 是的 | 是的 | 是的 | 是的 | 是的 | 是的 |
| 400 | 是的 | 不 | 不 | 不 | 不 | 不 |
| 450 | 不 | 不 | 不 | 不 | 是的 | 不 |
屈服强度
型钢的屈服强度取决于其牌号, 牌号越高,屈服应力越高. 热轧和加工型材的屈服强度根据型材厚度的不同而变化. 较厚的钢型材通常比相同等级的较薄钢型材具有较低的屈服强度.
冷成型型材是该规则的例外,并且每个钢种具有一致的屈服强度, 与截面厚度无关. 截面屈服强度和极限强度 (拉伸) 强度值可以使用表计算 2.1 在AS 4100:2020.
在 SkyCiv AS 中选择一个部分 4100 钢构件设计
的 SkyCiv AS 4100:2020 钢构件设计 工具允许用户从 SkyCiv 数据库中选择标准部分或设计完全自定义部分. 当选择标准部分时, 使用 AS 根据钢级自动计算翼缘和腹板屈服强度 4100 桌子 2.1. 当选择自定义部分时, 用户必须输入翼缘和腹板屈服强度值. 如果用户指定,标准型材也可以与定制钢种一起使用.

区段容量
弯曲
截面弯矩能力
作为 4100:2020 计算型钢的弯矩能力如下:
\(M_s = f_y*Z_e)
其中 f和 是材料的屈服应力, 和ZË 是有效截面模量. 形状的截面模量是量化形状抗弯强度的几何特性. 在结构工程中,我们使用两个截面模量值, 的 松紧带 (与) 和 塑料 (小号) 截面模量. 注意, 其他地区的设计标准有时会互换弹性截面模数和塑性截面模数的符号.
弹性截面模量假设整个截面 (形状) 在弯曲下保持弹性, 即. 截面没有任何部分超过屈服强度 (F和) 材料的. 当截面中的极端纤维时,通常会发生这种情况 (顶部/btm) 达到屈服. 截面的弹性截面模量计算如下:
\(Z = \frac{一世}{和}\)
其中 I 是面积二阶矩,y 是形状的几何质心.
塑性截面模量假设整个截面达到材料在弯曲下的屈服强度, 这意味着部分截面将超过屈服强度并经历塑性变形. 截面的塑性截面模量计算如下:
\(S = A_C*y_C + A_T*y_T \)
其中AC 和一个Ť 是塑性中性轴两侧的面积 (PNA), 和yC / 和Ť 是从 PNA 到这些区域质心的距离. 注意, PNA 位置等于对称形状的几何质心位置,但会 不是 等于不对称形状的几何质心位置.
栏目分类
某些型钢在达到屈服强度之前可能会出现局部弯曲的情况, 意味着无法达到弹塑性截面模量的全部能力. 这通常发生在较大的, 更薄的形状, 更容易受到局部屈曲的影响. 作为 4100 使用有效截面模数 (她) 考虑局部屈曲的可能性并相应降低截面的弯曲能力的值. 作为 4100 将部分分为三类:
- 袖珍的: 紧凑型截面不易受局部屈曲影响,可以充分发挥其性能 塑性力矩能力, 意味着整个截面在弯曲下可以达到其屈服强度.
- 非紧凑型: 非致密截面可以在截面的极端纤维处达到屈服强度 (弹性力矩能力) 但在局部屈曲发生之前无法达到其塑性力矩能力.
- 修长: 在发生局部屈曲之前,细长截面无法达到其弹性力矩能力.

断面细长度
作为 4100 通过计算截面内每个单元的长细度并找到 “关键要素” 首先会在压缩时弯曲. 对于 I 型截面, 元素细分如下所示. 仅计算突出元素的细长值, 即. 双向不受约束的元件. 翼缘和腹板之间的连接面积 (如下图白色所示) 在两个方向上受到限制,因此不易受到局部屈曲的影响.
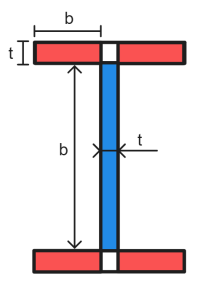
扁平元件的长细度计算如下:
\(λ_e = \frac{b}{Ť}\sqrt{\压裂{f_y}{250}}\)
作为 4100 桌子 5.2 包含塑性和屈服细长极限值 (λEP & λ哎呀) 用于基于应力分布的压缩板单元, 边缘支撑和残余应力. 一个部分的关键元素是具有最高值的元素 λË / λ哎呀 比率. 该元素的细长值 (λË) 用于对整个部分进行分类 (称为 λs).
如果 λs ≤ λsp 断面紧凑. 对于紧凑型截面, 有效截面模量计算如下:
\(Z_e = Z_c = 最小值(小号,1.5*与)\)
其中 S 是塑性截面模量, Z 为截面的弹性截面模量. 术语ZC 与紧凑截面的有效截面模数互换使用.
如果 λsp ≤ λs ≤ λ他的 该截面是非紧凑的. 对于非紧凑截面, 有效截面模量计算如下:
\(Z_e = Z + [(\压裂{l_{他的} – l_{s}}{l_{他的} – l_{sp}})(Z_c-Z)]\)
其中ZC 是紧凑截面的有效截面模量.
如果 λs > λ他的 截面细长. 对于具有均匀压缩的平板元件的细长截面, 有效截面模量计算如下:
\(Z_e = Z(\压裂{l_{他的}}{λ_s})\)
注意, 无支撑边缘处有张力的圆形空心型材或平板元件的有效截面模量的计算方式不同. 参考AS 4100 条款 5.2.5 了解更多信息.
计算 SkyCiv AS 中的截面弯曲能力 4100 钢构件设计
的 SkyCiv AS 4100:2020 钢构件设计 该工具可计算绕两个主轴的正向和负向弯曲的细长分类和截面弯曲能力. 细长分类检查结果 230 PFC详细说明如下.

很明显,根据弯曲方向的不同,长细值和截面分类也不同. 这是因为应力分布和边缘支撑值会根据哪些元素处于压缩或拉伸状态而变化, 导致不同的细长极限值.
一旦截面细长已知, 该模块计算截面弯矩能力 (检查锚容量) 围绕每个主轴进行正向和负向弯曲. 对于对称形状 (例如 I 部分), 这个值在正负方向上是相同的. 不对称形状将在正向和负向弯曲方向上具有不同的截面弯曲能力, 如那个 230 PFC 如下例所示.

剪力
截面剪切能力
作为 4100 仅考虑截面的腹板对其抗剪能力的贡献. 因此截面的抗剪承载力 (电压) 等于腹板剪切能力. 如果需要,可以在截面上添加垂直加强筋以增加其抗剪能力. 根据腹板上的剪应力分布是均匀还是不均匀,腹板的承载力计算方式有所不同. 对于标准截面形状,假设有以下剪切应力分布:
| 形状 | 剪应力分布 | |
|---|---|---|
| Y方向 | Z方向 | |
| I 型截面 | 制服 | 不均匀 |
| T 型截面 | 不均匀 | 不均匀 |
| 平行法兰槽钢 (全氟辛烷磺酸) | 制服 | 不均匀 |
| 角度 | 不均匀 | 不均匀 |
| 右侧/右侧 | 不均匀 | 不均匀 |
| CHS | 制服 | 制服 |
均匀剪应力分布
剪应力分布均匀截面的抗剪承载力 (Vü) 根据腹板的细长计算不同. 对于非细长的网络, 容量计算如下:
\(\压裂{d_p}{t_w} ≤ \frac{82}{\sqrt{\压裂{f_y}{250}}}\rightarrow V_u = V_w = 0.6*f_y*A_w\)
圆形空心 V 形截面的注意事项w = 0.36*f和*一个.
当截面腹板细长时, 容量计算如下:
\(\压裂{d_p}{t_w} > \压裂{82}{\sqrt{\压裂{f_y}{250}}}\rightarrow V_u = V_b = α_v*V_w\)
\(α_v = \left[\压裂{82}{(\压裂{d_p}{t_w})\sqrt{\压裂{f_y}{250}}}\对]^2)
哪里 dp 是网络面板的净深度 (即. 深度(不包括法兰)), Ťw 是腹板的厚度, F和 是腹板屈服强度,Aw 是腹板的总截面积. 注Aw 焊接截面和热轧截面的计算方式不同. 对于热轧型材, 一个w 将腹板深度作为整个截面深度 (d). 对于焊接型材, 一个w 仅采用翼缘之间的净腹板深度 (dp). 矩形空心型材也采用dp 用于计算Aw.
非均匀剪切应力分布
剪应力分布均匀截面的抗剪承载力 (Vv) 计算如下:
\(V_v = \frac{2*V_u}{0.9+\剩下(\压裂{F*_{虚拟机}}{F*_{弗吉尼亚州}}\对)} ≤ V_u\)
其中Vü 是具有均匀剪切应力分布的截面剪切能力,f*虚拟机 /F*弗吉尼亚州 是腹板中最大设计剪应力与平均设计剪应力之比.
计算 SkyCiv AS 中的剪切能力 4100 钢构件设计
它计算截面在两个主轴上的抗剪能力. 短轴 (与) 抗剪承载力是使用截面翼缘的贡献来计算的, 排除本节网络的任何贡献. 剪切承载力计算结果 200 UB 22.3 详细如下.

压缩
截面压缩能力
作为 4100 计算压缩能力 (ñs) 同心加载截面如下:
\(N_s = k_f*A_n*f_y\)
其中 kF 是截面的形状系数, 一个ñ 是横截面的净面积 (总面积,不包括穿透/孔洞) 和 f和 是截面的屈服强度. 截面的形状系数表示在发生局部屈曲之前,截面的压缩能力有多少. 形状因数计算如下:
\(k_f = \frac{A_e}{A_g}\)
其中AG 是截面的总面积, 和一个Ë 是个 “有效面积” 该部分的, 即. 该部分的总面积减去任何 “无效的” 受压区域. 无效区域是在压缩下达到屈服强度之前会弯曲的部分. 有效面积的计算方法是: “有效宽度” 截面内的每个平板单元并使用这些调整后的宽度值重新计算截面面积. 平板单元的有效宽度计算如下:
\(b_e = b\left(\压裂{l_{哎呀}}{l_{Ë}}\对) ≤ b\)
在哪里:
\(λ_e = \frac{b}{Ť}\sqrt{\压裂{f_y}{250}}\)
注意, 大多数设计软件使用截面屈服强度进行单元细长计算, 而不是腹板/法兰的特定屈服强度. 这总是会提供保守的结果. b 值用于 λË 计算与用于弯曲截面长细度检查的尺寸相同 (法兰围绕腹板分开), 但 b 用于 bË 计算结果为翼缘/腹板总宽度. λ哎呀 取自AS 4100 桌子 6.2.4, 取决于该元件的边缘支撑和残余应力.
圆形空心型材的有效宽度计算公式如下:
\(d_e = 分钟(d_{的}\sqrt{\剩下(\压裂{l_{哎呀}}{l_{Ë}}\对)}, d_{的}\剩下(\压裂{3*l_{哎呀}}{l_{Ë}}\对)^ 2) ≤ d_{的}\)
在哪里:
\(λ_e = \left(\压裂{做}{Ť}\对)\剩下(\压裂{f_y}{250}\对)\)
计算 SkyCiv AS 中的截面压缩能力 4100 钢构件设计
形状因数和截面压缩能力 (ñs) 针对标准澳大利亚路段和自定义用户定义路段进行计算. 610UB 截面压缩能力计算结果 125 详细如下.

张力
截面抗拉能力
作为 4100 计算受拉杆件的承载力 (Nt) 如下:
\(N_t = 最小值(一个_{G}*F_{和}\; ,\; 0.85*k_t*A_n*f_u)\)
其中AG 是截面的总面积, 一个ñ 是横截面的净面积 (总面积,不包括穿透/孔洞), F和 是截面的屈服强度, Fü 是拉伸力 (最终的) 截面强度和 kŤ 是拉力分布修正系数. kŤ 设计中使用的不同取决于截面形状和连接类型. 提供均匀力分布的连接导致 kŤ 的因素 1.0, 力分布不均的连接会导致 kŤ 之间的因素 0.75-1.0.
计算 SkyCiv AS 中的张力能力 4100 钢构件设计
我们的工具允许用户指定 k 部分Ť 设计使用价值. 较低的 kŤ 值将导致截面张力能力降低. SkyCiv AS 4100 构件设计计算器假定该部分不存在明显的孔, 因此Añ 被视为等于 AG. 610UB 截面抗拉能力计算结果 125 详细如下.

会员容量
弯曲
构件弯矩能力
钢构件的弯矩能力并不总是由截面的弯矩能力决定 (ms). 这是因为在达到该部分的容量之前,成员可以通过其他方法失败. 横向扭转屈曲是长/无约束钢构件的常见失效方法, 当截面旋转远离其主轴时会发生这种情况 (朝向其短轴) 减少弯曲方向的力矩能力.

作为 4100 包含计算名义会员容量的指南 (mb), 影响钢构件截面能力的因素 (ms) 考虑成员细长和约束条件的影响.
具有完全横向约束的成员
关键法兰
截面的临界翼缘是在屈曲过程中偏转最远的翼缘, 最终导致横向扭转屈曲失效. 这通常是构件的压缩凸缘. 垂直载荷下标准型材的关键法兰位置如下所示.

完全横向约束
具有高旋转/横向刚度的较短构件在负载下不太可能旋转出平面, 减少横向扭转屈曲失效的可能性. 如果构件足够短/刚性,它将能够达到其截面力矩容量 (ms) 在另一种故障方法发生之前. 满足此条件的会员被视为具有 “完全横向约束”.
\(满的 \; 侧 \; C3.1.2.1-6 \; \rightarrow M_b = M_s\)
作为 4100 条款 5.3.2 提供有关计算会员完全横向约束限制的指导. 圆形空心型材 (CHS) 和方形空心截面 (SHS) 不易受到横向扭转屈曲的影响, 因为它们具有高横向/扭转刚度和绕两个轴的等截面力矩能力. 因此,无论构件长度如何,通常假定这些部分能够实现完全横向约束.
持续横向约束
沿其整个长度对关键凸缘具有连续约束的构件被视为具有 “持续横向约束”. 在计算构件弯曲能力时,连续横向约束被认为等同于完全横向约束 (mb).
没有完全横向约束的成员
未实现完全侧向约束的构件的弯矩能力计算如下:
\(M_b = α_m*α_s*M_s ≤ M_s\)
其中 α米 是矩修正因子,αs 是细长折减系数. 作为 4100 条款 5.6 概述计算 α 的过程米 和αs.
短轴杆件弯曲能力
绕其短轴弯曲的构件的弯曲能力 (mb) 等于短轴截面容量 (ms) 绕该轴. 短轴截面承载能力反映的是截面绕任意轴所能达到的最小承载能力, 因此该构件不能从该轴旋转到不利的方向.
计算 SkyCiv AS 中的构件弯曲能力 4100 钢构件设计
该工具执行全面的横向约束检查并计算正负弯曲的绕两个主轴的构件弯矩能力. 用户还可以选择 “持续横向约束” 绕过完全横向约束检查. 3m 长 200UB22.3 的构件弯曲能力计算结果详述如下.

注意, 该计算器假设 βs = -1.0 在所有计算中.
压缩
成员压缩能力
构件的轴向压缩能力还受其长度的影响, 侧向刚度和约束条件. 无拘无束, 较长的构件可能会因截面前的弯曲屈曲而失效 (壁球) 容量已达到. 作为 4100 包含计算名义会员容量的指南 (ñC), 影响压缩段容量的因素 (ñs) 考虑成员细长和约束条件的影响.
\(N_c = α_c*N_s ≤ N_s\)
其中 αC 是杆件细长折减系数. 条款 6.3.3 的AS 4100 提供计算 α 的指导C. 必须检查两个轴的杆件压缩能力以找到控制值
\(α_c = ξ\left[1 – \sqrt{ 1 – \剩下( \压裂{ 90}{ETC} \对)^ 2} \对]\)
\(\xi = \frac{ \剩下( \压裂{ \拉姆达 }{90} \对)^ 2 + 1 + \和 }{2 \剩下( \压裂{ \拉姆达 }{90} \对)^ 2}\)
\(\lambda = \lambda_n + α_aα_b\)
\(小时= 0.00326(\拉姆达 – 13.5) \geq 0\)
\(\alpha_a = \frac{2100(\拉姆达_n – 13.5)}{\lambda_n^2 – 15.3\拉姆达_n + 2050}\)
\(\lambda_n = \left( \压裂{这}{[R} \对) \sqrt{k_f} \sqrt{\压裂{f_y}{250}}\)
在哪里 (大号Ë) r 是屈曲相关轴的有效长度和回转半径. 一种b 是成员部分常量, 这是使用 AS 确定的 4100 桌子 6.3.3. 该计算模块对α赋值所采用的逻辑b 概述如下:
| ķF | 残余应力 | 节类型 / 形状 | ŤF ≤ 40? | 一种乙 |
|---|---|---|---|---|
| < 1 | 人力资源 | I 型截面 | 是的 | 0 |
| 没有 | 1.0 | |||
| 其他 | – | 1.0 | ||
| 硬件 | I 型截面 | 是的 | 0.5 | |
| 没有 | 1.0 | |||
| RHS / SHS | – | 0 | ||
| 其他 | – | 1.0 | ||
| CF | 任何 | – | -0.5 | |
| = 1 | 人力资源 | I 型截面 | 是的 | 0 |
| 没有 | 1.0 | |||
| 其他 | – | 0.5 | ||
| 硬件 | I 型截面 | – | 0 | |
| RHS / SHS | – | 0 | ||
| 其他 | – | 0.5 | ||
| CF | 任何 | – | -0.5 |
注意:
– 假设空心截面未消除应力,以计算构件截面常数 (一种b).
– 在计算构件截面常数时,假设 WB/WC 截面和所有定制截面均由火焰切割板制成 (一种b).
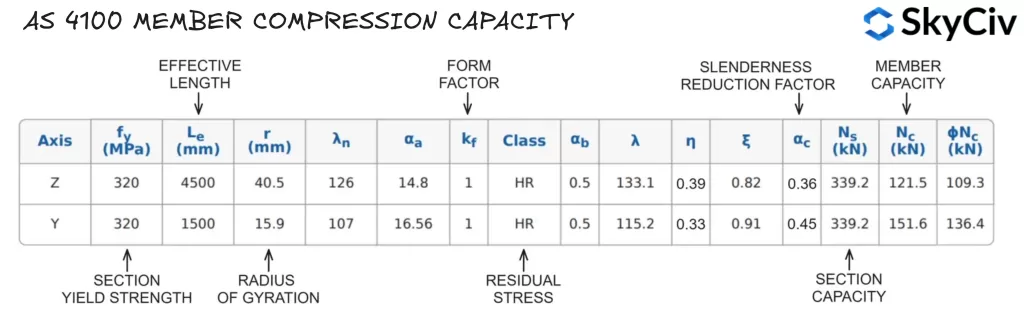
计算 SkyCiv AS 中的成员压缩容量 4100 钢构件设计
该工具根据用户指定的约束长度和有效长度系数计算两个主轴的构件压缩能力. Z 轴和 Y 轴无约束长度分别为 4500mm 和 1500mm 的 200UB22.3 的构件压缩能力计算结果 (分别) 详细如下.
SkyCiv 结构设计软件
SkyCiv 提供广泛的结构分析和工程设计软件, 包含:
- AS / NZS 1664 铝设计
- AS / NZS 4600 檩条设计
- 作为 3600 混凝土剪力墙设计
- 作为 2870 住宅楼板等级设计
- AS / NZS 1576 脚手架设计
- 作为 4055 风荷载计算器
软件开发师 | 结构工程师
ng (民用), 工程学士学位 (软件)
领英



