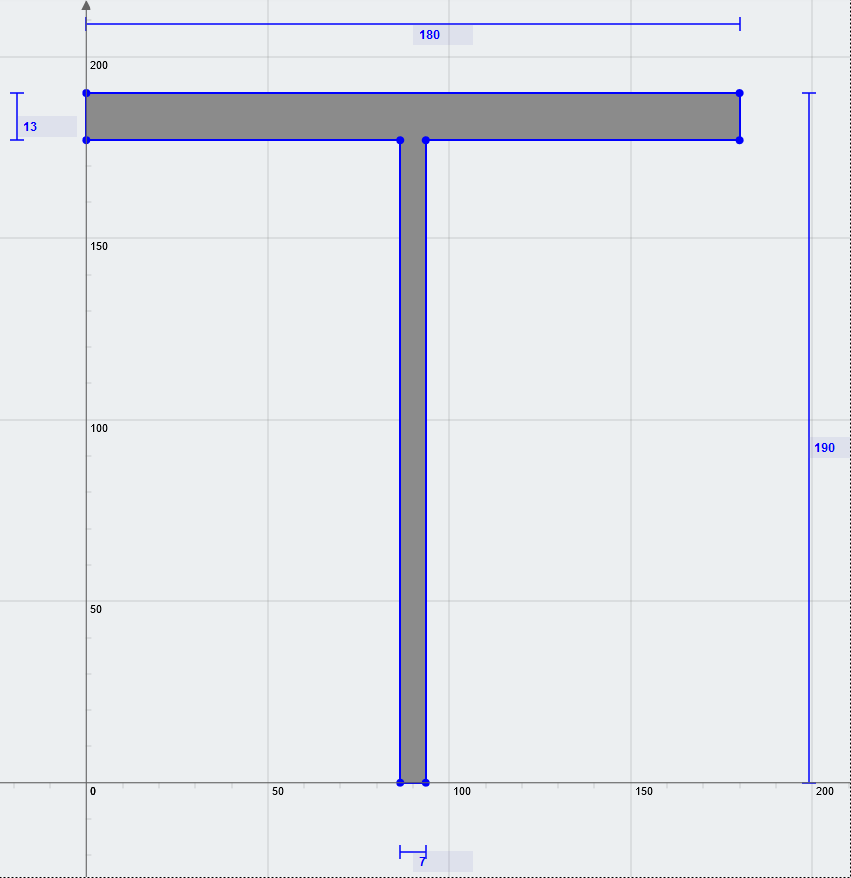
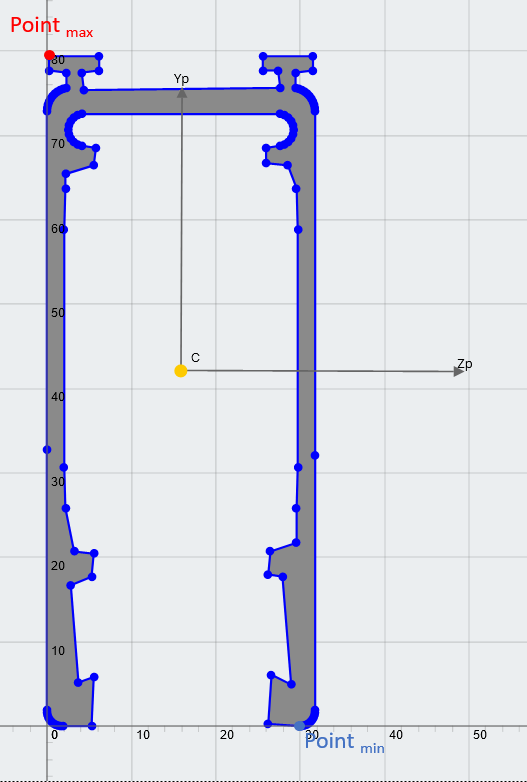
例 1
确定受合力作用的 T 形截面的应力.
| 截面尺寸 | 几何特性 | 势力 |
 |
惯性矩
最大和最小距离
剪切特性
扭转力
|
|
结果比较
| 结果 | 位置 | SkyCiv SB分析 | 手册 | 第三方 |
| 主要应力 (兆帕) | ||||
| 轴向的 | 最高 | 2.794 | \(\压裂{区}{轴向的}= 分数{10·1000}{3579} = 2.794\)
(0.00%) |
2.794
(0.00%) |
| 分 | 2.794 | \(\压裂{区}{轴向的}= 分数{10·1000}{3579} = 2.794\)
(0.00%) |
2.794
(0.00%) |
|
| 弯曲 Y | 最高 | 14.234 | \(\压裂{弯曲 Y}{我_y/y_{最高}}= 分数{1·100万}{6.32306·10^6/90} =14.234\)
(0.00%) |
14.234
(0.00%) |
| 分 | -14.234 | \(\压裂{弯曲 Y}{我_y/y_{分}}= 分数{1·100万}{6.32306·10^6/-90} =-14.234\)
(0.00%) |
-14.234
(0.00%) |
|
| 弯曲 Z | 最高 | 3.723 | \(\压裂{弯曲 Z}{我_z/z_{最高}}= 分数{1·100万}{1.05786·10^7/39.3877} =3.723\)
(0.00%) |
3.723
(0.00%) |
| 分 | -14.237 | \(\压裂{弯曲 Z}{我_z/z_{分}}= 分数{1·100万}{1.05786·10^7/-150.6123} =-14.237\)
(0.00%) |
-14.237
(0.00%) |
|
| 合成剪切 Y | 最高 | 1.123 | \(\压裂{剪切Y·Q_z}{I_z·t}= 分数{1·1000·7.93943·10^4}{1.05786·10^7·7} = 1.072\)
(4.54%) |
1.120
(0.26%) |
| 合成剪切 Z | 最高 | 0.698 | \(\压裂{剪切Z·Q_y}{I_y·t}= 分数{1·1000·5.25658·10^4}{6.32306·10^6·13} = 0.639\)
(8.45%) |
0.709
(1.57%) |
| 扭转力 | 最高 | 9.956 | \(\压裂{r_{最高}}{Ĵ}= 分数{0.1·1000000·13.5357}{1.46870·10^5} = 9.216\)
(7.43%) |
9.570
(3.87%) |
例 2
确定受合力作用的截面的应力.
| 截面尺寸 | 几何特性 | 势力 |
 |
惯性矩
最大和最小距离
剪切特性 剪Y
剪Z
扭转力
|
|
结果比较
| 结果 | 位置 | SkyCiv SB分析 | 手册 | 第三方 |
| 主要应力 (兆帕) | ||||
| 轴向的 | 最高 | 18.729 | \(\压裂{区}{轴向的}= 分数{10·1000}{533.9368} = 18.729\)
(0.00%) |
18.73
(0.00%) |
| 分 | 18.729 | \(\压裂{区}{轴向的}= 分数{10·1000}{533.9368} = 18.729\)
(0.00%) |
18.793
(0.00%) |
|
| 弯曲 Y | 最高 | 166.538 | \(\压裂{M_y·\cos(\α)}{\压裂{I_y}{z_{最高}}}+\压裂{M_y·\sin(\α)}{\压裂{I_z}{y_{最高}}}= 分数{1000000·\cos(-0.1562^ 圆)}{\压裂{3.84955·10^5}{-42.0526}}+\压裂{1000000·\sin(-0.1562^ 圆)}{\压裂{9.59281·10^4}{14.1016}}=166.694\)
(0.00%) |
166.5
(0.00%) |
| 分 | -165.951 | \(\压裂{M_y·\cos(\α)}{\压裂{I_y}{z_{分}}}+\压裂{M_y·\sin(\α)}{\压裂{I_z}{y_{分}}}= 分数{1000000·\cos(-0.1562^ 圆)}{\压裂{3.84955·10^5}{30.7351}}+\压裂{1000000·\sin(-0.1562^ 圆)}{\压裂{9.59281·10^4}{-15.9392}}=166.045\)
(0.00%) |
-166.0
(0.00%) |
|
| 弯曲 Z | 最高 | 97.189 | \(\压裂{M_z·\cos(\α)}{\压裂{I_z}{y_{最高}}}+\压裂{M_z·\sin(\α)}{\压裂{I_y}{z_{最高}}}= 分数{1000000·\cos(-0.1562^ 圆)}{\压裂{3.84955·10^5}{37.2424}}+\压裂{1000000·\sin(-0.1562^ 圆)}{\压裂{9.59281·10^4}{-15.7027}}=97.19\)
(0.00%) |
97.19
(0.00%) |
| 分 | -109.639 | \(\压裂{M_z·\cos(\α)}{\压裂{I_z}{y_{分}}}+\压裂{M_z·\sin(\α)}{\压裂{I_y}{z_{分}}}= 分数{1000000·\cos(-0.1562^ 圆)}{\压裂{3.84955·10^5}{-42.0526}}+\压裂{1000000·\sin(-0.1562^ 圆)}{\压裂{9.59281·10^4}{14.1016}}=-109.64\)
(0.00%) |
-109.6
(0.00%) |
|
| 合成剪切 Y | 最高 | 4.302 | \(\压裂{ShearY·\cos(\α)Qz}{伊兹普·t}+\压裂{ShearZ·\cos(\α)·Qy}{yp·t}= 分数{1000·\cos(-0.1562^ 圆)·6533.7159}{{3.84955·10^5·3.9624}}+\压裂{1000·\sin(-0.1562^ 圆)·4.2994}{9.59281·10^4·3.9624}=4.283\)
(0.44%) |
4.297
(0.12%) |
| 合成剪切 Z | 最高 | 16.629 | \(\压裂{ShearZ·\sin(\α)Qz}{伊兹普·t}+\压裂{ShearZ·\cos(\α)·Qy}{yp·t}= 分数{1000·\sin(-0.1562^ 圆)·929.3201}{{3.84955·10^5·2.8145}}+\压裂{1000·\cos(-0.1562^ 圆)·3337.6406}{9.59281·10^4·2.8145}=12.36\)
(25.67%) |
17.37
(4.46%) |
| 扭转力 | 最高 | 30.418 | \(\压裂{r_{最高}}{Ĵ}= 分数{0.1·1000000·4.6293}{1513.65} = 30.584\)
(0.55%) |
31.98
(5.14%) |
