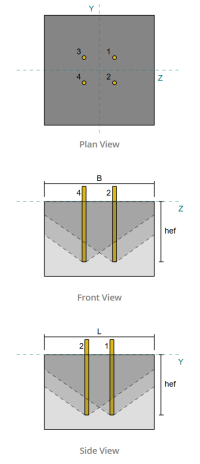
基本板设计示例使用AISC 360-22 和ACI 318-19
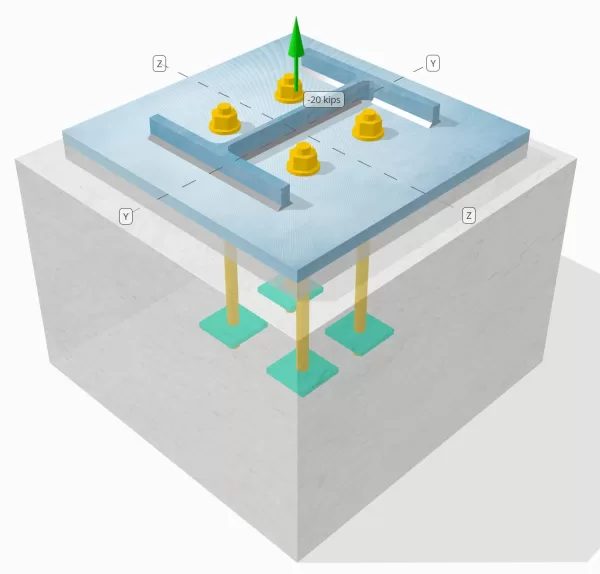
问题陈述
确定设计的列板连接是否足以容纳20千座张力负载.
给定数据
柱:
列部分: W12x53
列区域: 15.6 在2
列材料: A992
底盘:
基板尺寸: 18 在x 18 在
基板厚度: 3/4 在
底板材料: A36
灌浆:
灌浆厚度: 1 在
具体:
混凝土尺寸: 22 在x 22 在
混凝土厚度: 15 在
混凝土材料: 4000 压力
破裂或无裂缝: 破裂
锚:
锚直径: 3/4 在
有效嵌入长度: 12 在
嵌入式板宽: 3 在
嵌入式板厚度: 1/4 在
锚偏移距离列的面板网络的距离: 2.8275 在
焊缝:
焊缝尺寸: 1/4 在
填充金属分类: E70XX
锚数据 (从 SkyCiv计算器):
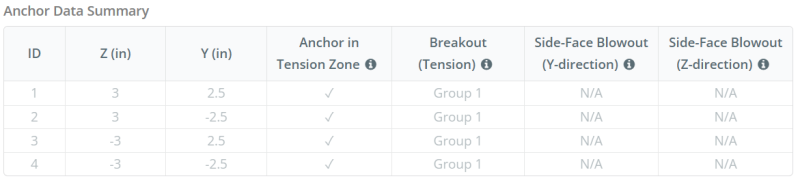
SkyCiv 免费工具中的模型
立即使用我们的免费在线工具对上面的底板设计进行建模! 无需注册.
定义
负载路径:
当底板受到抬高时 (拉伸) 军队, 这些力被转移到锚杆上, 这反过. 弯曲动作可以看到为 悬臂弯曲 发生在列的法兰或网络周围, 取决于锚定位的位置.
在里面 SkyCiv 底板设计软件, 只有位于 锚张带 被认为有效抵抗提升. 该区域通常包括列法兰或网络附近的区域. 该区域以外的锚点不会导致抗拉力抵抗力，并且被排除在隆起计算之外.
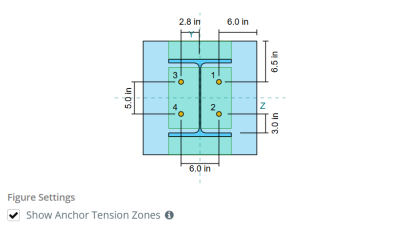
确定基本板的有效区域，以抵抗弯曲, 一个 45-学位分散 从每个锚杆的中心线朝向圆柱面假设. 这个分散定义了 有效的焊接长度 并帮助建立 有效的弯曲宽度 盘子的.
该假设通过近似抬高力如何通过板来简化基板分析.
锚群:
的 SkyCiv 底板设计软件 包括一个直观的功能，该功能标识哪些锚定为评估的锚点组的一部分 混凝土突破 和 混凝土侧侧电子面井喷 失败.
一个 锚群 由具有相似有效嵌入深度和间距的多个锚组成, 并且足够近，以至于他们 预计电阻区重叠. 当锚分组时, 它们的能力合并以抵抗施加到该组的总张力.
不符合分组标准的锚被视为 单锚. 在这种情况下, 仅检查单个锚点上的张力力与其自身的有效阻力区域检查.
分步计算
检查一下 #1: 计算焊接容量
开始, 我们需要计算每个锚的负载和每个锚的有效焊接长度. 有效的焊接长度取决于最短长度 45°分散, 受实际焊接长度和锚固间距的约束.
为此计算, 锚被归类为 结束锚 要么 中间锚. 最终锚位于行的末端或锚列的末端, 中间锚位于它们之间. 每种计算方法都不同，并取决于列的几何形状. 在这个例子中, 网上有两个锚, 两者都被归类为最终锚.
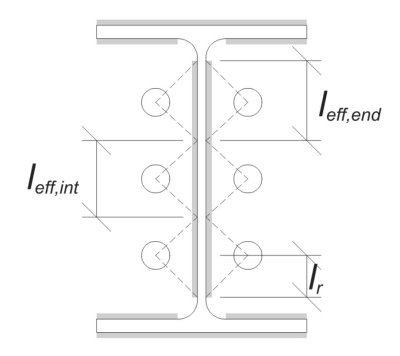
最终锚, 有效的焊缝长度受锚式中心线到圆柱圆角的可用距离的限制. 45°色散不得延伸到这个边界之外.
\(
l_r = \dfrac{d_{col} – 2t_f – 2r_{col} – s_y(n_{a,side} – 1)}{2} = \dfrac{12.1 \, \text{in} – 2 \times 0.575 \, \text{in} – 2 \times 0.605 \, \text{in} – 5 \, \text{in} \times (2 – 1)}{2} = 2.37 \, \text{in}
\)
内侧, 有效长度受锚间距的一半限制. 端锚的总有效焊接长度是外部和内部长度的总和.
\(
l_{eff,end} = \min(d_o, 0.5s_y) + \min(d_o, l_r)
\)
\(
l_{eff,end} = \min(2.8275 \, \text{in}, 0.5 \times 5 \, \text{in}) + \min(2.8275 \, \text{in}, 2.37 \, \text{in}) = 4.87 \, \text{in}
\)
对于这个例子, 的 最终有效焊接长度 因为网络锚是端锚的有效长度.
\(
l_{eff} = l_{eff,end} = 4.87 \, \text{in}
\)
下一个, 让我们计算 每个锚负载. 给定的四组 (4) 锚点, 每个锚的负载是:
\(
T_{u,anchor} = \dfrac{N_x}{n_{a,t}} = \dfrac{20 \, \text{kip}}{4} = 5 \, \text{kip}
\)
使用计算的有效焊接长度, 现在我们可以确定 焊缝上的每单位长度要求.
\(
r_u = \dfrac{T_{u,anchor}}{l_{eff}} = \dfrac{5 \, \text{kip}}{4.87 \, \text{in}} = 1.0267 \, \text{kip/in}
\)
现在, 我们将使用 AISC 360-22, 第J2.4章 计算圆角焊缝的设计强度.
由于施加的载荷纯粹是轴向张力, 角度 \(\theta\) 被视为90°, 并根据 AISC 360-22 情商. J2-5.
\(
k_{ds} = 1.0 + 0.5(\sin(\theta))^{1.5} = 1 + 0.5 \times (\sin(1.5708))^{1.5} = 1.5
\)
最后, 我们将申请 AISC 360-22 情商. J2-4 确定 每单位长度的圆角焊缝的设计强度.
\(
\phi r_n = \phi 0.6 F_{exx} E_{w,web} k_{ds} = 0.75 \times 0.6 \times 70 \, \text{ksi} \times 0.177 \, \text{in} \times 1.5 = 8.3633 \, \text{kip/in}
\)
以来 1.0267 KPI < 8.3633 KPI, 焊接容量是 充足的.
检查一下 #2: 计算由于张力负载而导致的基本板弯曲屈服能力
使用t他每个锚和O负载从锚的中心到柱面的FFSET距离 (充当负载偏心), 应用于基板的力矩可以使用 悬臂 假设.
\(
M_u = T_{u,\text{anchor}} e = 5 \, \text{kip} \times 2.8275 \, \text{in} = 14.137 \, \text{kip} \cdot \text{in}
\)
下一个, 使用计算d有效的焊接长度来回m先前的支票作为弯曲宽度, 我们可以计算 是一个设计模块，用于根据上部结构载荷设计扩展基础 使用底板的 AISC 360-22, 方程 2-1:
\(
\phi M_n = \phi F_{y,\text{bp}} Z_{\text{eff}} = 0.9 \times 36 \, \text{ksi} \times 0.68484 \, \text{in}^3 = 22.189 \, \text{kip} \cdot \text{in}
\)
在哪里,
\(
Z_{\text{eff}} = \dfrac{l_{\text{eff}} (t_{\text{bp}})^2}{4} = \dfrac{4.87 \, \text{in} \times (0.75 \, \text{in})^2}{4} = 0.68484 \, \text{in}^3
\)
以来 14.137 小鸡 < 22.189 小鸡, 基板弯曲屈服能力为 充足的.
检查一下 #3: 计算锚杆拉伸能力
评估锚杆的拉伸能力, 我们将使用 ACI 318-19 方程 17.6.1.2.
第一, 我们确定 指定的拉伸强度 锚钢. 这是允许的最低值 ACI 318-19 条款 17.6.1.2, 参考物质特性 AISC 360-22 表J3.2.
\(
f_{\text{uta}} = \min \left( 0.75 F_{u,\text{anc}}, 1.9 F_{y,\text{anc}}, 125 \right) = \min \left( 0.75 \times 120 \, \text{ksi}, 1.9 \times 92 \, \text{ksi}, 125.00 \, \text{ksi} \right) = 90 \, \text{ksi}
\)
下一个, 我们计算 有效的横截面区域 锚杆. 这是基于 ACI 318-19 评论条款R17.6.1.2, 哪个考虑线程几何形状. 每英寸的线数取自 ASME B1.1-2019表 1.
\(
A_{se,N} = \dfrac{\pi}{4} \left( d_a – \dfrac{0.9743}{n_t} \right)^2 = \dfrac{\pi}{4} \times \left( 0.75 \, \text{in} – \dfrac{0.9743}{10 \, \text{in}^{-1}} \right)^2 = 0.33446 \, \text{in}^2
\)
这些值, 我们申请 ACI 318-19 方程 17.6.1.2 计算 设计拉伸强度 锚杆.
\(
\phi N_{sa} = \phi A_{se,N} f_{\text{uta}} = 0.75 \times 0.33446 \, \text{in}^2 \times 90 \, \text{ksi} = 22.576 \, \text{kip}
\)
回想先前计算的 每个锚的张力负载:
\(
N_{ua} = \dfrac{N_x}{n_{a,t}} = \dfrac{20 \, \text{kip}}{4} = 5 \, \text{kip}
\)
以来 5 基普 < 22.576 基普, 锚杆拉伸能力为 充足的.
检查一下 #4: 计算张力的混凝土突破能力
在计算突破能力之前, 我们必须首先确定成员是否有资格 狭窄的成员. 根据 ACI 318-19 条款 17.6.2.1.2, 该成员符合狭窄成员的标准. 因此, 经过修改的有效嵌入长度必须用于计算.
确定 修改的有效嵌入长度, h’ef, 锚群是:
\(
h’_{\text{ef}} = 5.667 \, \text{in}
\)
使用 ACI 318-19 条款 17.6.2, 我们计算 最大投影混凝土锥体区域 对于单个锚点, 基于修改的有效嵌入长度.
\(
A_{N_{co}} = 9 \left( h’_{ef,g1} \right)^2 = 9 \times \left( 5.6667 \, \text{in} \right)^2 = 289 \, \text{in}^2
\)
相似地, 我们使用修改的有效嵌入长度来计算 实际投影混凝土锥体 锚群.
\(
A_{N_c} = \min \left( n_{a,g1} A_{N_{co}}, L_{N_c} B_{N_c} \right) = \min \left( 4 \times 289 \, \text{in}^2, 22 \, \text{in} \times 22 \, \text{in} \right) = 484 \, \text{in}^2
\)
在哪里,
\(
L_{N_c} = \min \left( c_{\text{left},g1}, 1.5 h’_{\text{ef},g1} \right)
+ \left( \min \left( s_{\text{sum},z,g1}, 3 h’_{\text{ef},g1} \left( n_{z,g1} – 1 \right) \right) \right)
+ \min \left( c_{\text{right},g1}, 1.5 h’_{\text{ef},g1} \right)
\)
\(
L_{N_c} = \min \left( 8 \, \text{in}, 1.5 \times 5.6667 \, \text{in} \right)
+ \left( \min \left( 6 \, \text{in}, 3 \times 5.6667 \, \text{in} \times \left( 2 – 1 \right) \right) \right)
+ \min \left( 8 \, \text{in}, 1.5 \times 5.6667 \, \text{in} \right)
\)
\(
L_{N_c} = 22 \, \text{in}
\)
\(
B_{N_c} = \min \left( c_{\text{top},g1}, 1.5 h’_{\text{ef},g1} \right)
+ \left( \min \left( s_{\text{sum},y,g1}, 3 h’_{\text{ef},g1} \left( n_{y,g1} – 1 \right) \right) \right)
+ \min \left( c_{\text{bottom},g1}, 1.5 h’_{\text{ef},g1} \right)
\)
\(
B_{N_c} = \min \left( 8.5 \, \text{in}, 1.5 \times 5.6667 \, \text{in} \right)
+ \left( \min \left( 5 \, \text{in}, 3 \times 5.6667 \, \text{in} \times \left( 2 – 1 \right) \right) \right)
+ \min \left( 8.5 \, \text{in}, 1.5 \times 5.6667 \, \text{in} \right)
\)
\(
B_{N_c} = 22 \, \text{in}
\)
下一个, 我们评估 基本的具体突破强度 使用一个锚 ACI 318-19 条款 17.6.2.2.1
\(
N_b = k_c \lambda_a \sqrt{\dfrac{f’_c}{\text{psi}}} \left( \dfrac{h’_{\text{ef},g1}}{\text{in}} \right)^{1.5} \, \text{lbf}
\)
\(
N_b = 24 \times 1 \times \sqrt{\dfrac{4 \, \text{ksi}}{0.001 \, \text{ksi}}} \times \left( \dfrac{5.6667 \, \text{in}}{1 \, \text{in}} \right)^{1.5} \times 0.001 \, \text{kip} = 20.475 \, \text{kip}
\)
在哪里,
- \(k_{c} = 24\) 用于预制锚栓
- \(\lambda = 1.0 \) 适用于正常的混凝土
现在, 我们通过计算 边缘效应因子 和 偏心率因子.
锚固组的最短边缘距离确定为:
\(
c_{a,\text{min}} = \min \left( c_{\text{left},g1}, c_{\text{right},g1}, c_{\text{top},g1}, c_{\text{bottom},g1} \right)
= \min \left( 8 \, \text{in}, 8 \, \text{in}, 8.5 \, \text{in}, 8.5 \, \text{in} \right) = 8 \, \text{in}
\)
根据 ACI 318-19 条款 17.6.2.4.1, 突破 边缘效应因子 是:
\(
\Psi_{ed,N} = \min \left( 1.0, 0.7 + 0.3 \left( \dfrac{c_{a,\text{min}}}{1.5 h’_{\text{ef},g1}} \right) \right)
= \min \left( 1, 0.7 + 0.3 \times \left( \dfrac{8 \, \text{in}}{1.5 \times 5.6667 \, \text{in}} \right) \right) = 0.98235
\)
由于张力负荷在锚群的质心上施加, 偏心率为零. 从而, 的 偏心率因子, 也来自条款 17.6.2.4.1, 是:
\(
\Psi_{ec,N} = \min \left( 1.0, \dfrac{1}{1 + \dfrac{2 e’_N}{3 h’_{\text{ef},g1}}} \right)
= \min \left( 1, \dfrac{1}{1 + \dfrac{2 \times 0}{3 \times 5.6667 \, \text{in}}} \right) = 1
\)
此外, 两者 开裂因子 和 分裂因子 被视为:
\(
\Psi_{c,N} = 1
\)
\(
\Psi_{cp,N} = 1
\)
然后, 我们结合了所有这些因素并使用 ACI 318-19 情商. 17.6.2.1b 评估 锚群的混凝土突破强度:
\(
\phi N_{cbg} = \phi \left( \dfrac{A_{N_c}}{A_{N_{co}}} \right) \Psi_{ec,N} \Psi_{ed,N} \Psi_{c,N} \Psi_{cp,N} N_b
\)
\(
\phi N_{cbg} = 0.7 \times \left( \dfrac{484 \, \text{in}^2}{289 \, \text{in}^2} \right) \times 1 \times 0.98235 \times 1 \times 1 \times 20.475 \, \text{kip} = 23.58 \, \text{kip}
\)
的 总施加负荷 在锚固组上是单个锚负荷的产物和锚的数量:
\(
N_{ua} = \left( \dfrac{N_x}{n_{a,t}} \right) n_{a,g1} = \left( \dfrac{20 \, \text{kip}}{4} \right) \times 4 = 20 \, \text{kip}
\)
以来 20 ps < 23.58 ps, 具体的突破能力是 充足的.
检查一下 #5: 计算锚推拉力
锚的拔出能力由嵌入端的电阻支配. 开始, 我们计算嵌入式板的轴承区域, 减去锚杆占用的区域后，这是净区域.
用于矩形嵌入式板, 的 轴承区 被计算为:
\(
A_{brg} = \left( \left( b_{embed\_plate} \right)^2 \right) – A_{rod} = \left( \left( 3 \, \text{in} \right)^2 \right) – 0.44179 \, \text{in}^2 = 8.5582 \, \text{in}^2
\)
在哪里,
\(
A_{rod} = \dfrac{\pi}{4} \left( d_a \right)^2 = \dfrac{\pi}{4} \times \left( 0.75 \, \text{in} \right)^2 = 0.44179 \, \text{in}^2
\)
下一个, 我们确定 基本的锚推力强度 使用 ACI 318-19 等式17.6.3.2.2a.
\(
N_b = 8 A_{brg} \left( f’_c \right) = 8 \times 8.5582 \, \text{in}^2 \times \left( 4 \, \text{ksi} \right) = 273.86 \, \text{kip}
\)
然后，我们应用适当的电阻因子和 拉裂因子:
- 对于 破裂 木结构, \(\Psi_{cp} = 1.0\)
- 对于 无裂 木结构, \(\Psi_{cp} = 1.4\)
使用这些, 我们计算 张力中的设计锚点拉力强度 每 ACI 318-19 方程 17.6.3.1.
\(
\phi N_{pn} = \phi \Psi_{c,p} N_b = 0.7 \times 1 \times 273.86 \, \text{kip} = 191.7 \, \text{kip}
\)
回想先前计算的 每个锚的张力负载:
\(
N_{ua} = \dfrac{N_x}{n_{a,t}} = \dfrac{20 \, \text{kip}}{4} = 5 \, \text{kip}
\)
以来 5 ps < 191.7 ps, 锚推拔出能力是 充足的.
检查一下 #6: 计算嵌入板弯曲能力
这是使用 SkyCiv底板设计软件 为了验证嵌入式板具有足够的弯曲能力，并且在施加的拔出载荷下不会产生.
第一, 我们确定免费的长度 (不支持) 嵌入式板的末端, 从支撑边缘到杆的脸部测量.
\(
b’ = \dfrac{b_{embed\_plate} – d_a}{2} = \dfrac{3 \, \text{in} – 0.75 \, \text{in}}{2} = 1.125 \, \text{in}
\)
下一个, 我们计算 弯矩 由均匀的轴承压力诱导. 这种压力表示从锚推动作转移到嵌入式板上的力.
\(
m_f = \dfrac{\left( \dfrac{T_a}{A_{brg}} \right) \left( b’ \right)^2}{2} = \dfrac{\left( \dfrac{5 \, \text{kip}}{8.5582 \, \text{in}^2} \right) \times \left( 1.125 \, \text{in} \right)^2}{2} = 0.36971 \, \text{kip}
\)
最后, 使用计算的力矩和给定的材料特性, 我们将确定 最小要求的板厚度 抵抗 弯曲屈服.
\(
t_{min} = \sqrt{\dfrac{4 m_f}{\phi F_{y\_ep}}} = \sqrt{\dfrac{4 \times 0.36971 \, \text{kip}}{0.9 \times 36 \, \text{ksi}}} = 0.21364 \, \text{in}
\)
回忆实际的嵌入式板厚度:
\(
t_{actual} = t_{embed\_plate} = 0.25 \, \text{in}
\)
以来 0.21364 在 < 0.25 在, 嵌入式板弯曲能力为 充足的.
检查一下 #7: 计算Y方向的侧面井喷容量
此计算不适用于此示例, 作为指定的条件 ACI 318-19 条款 17.6.4 没有满足. 因此, 不会发生Y方向的侧面井喷故障.
检查一下 #8: 计算Z方向的侧面井喷容量
此计算不适用于此示例, 作为指定的条件 ACI 318-19 条款 17.6.4 没有满足. 因此, 不会发生Z方向的侧面井喷故障.
设计概要
的 SkyCiv底板设计软件 可以自动为此设计示例生成逐步计算报告. 它还提供了执行的检查及其结果比率的摘要, 一目了然地使信息易于理解. 以下是示例摘要表, 报告中包括.
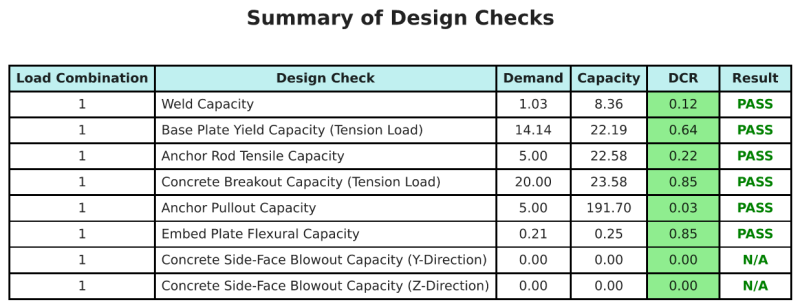
SkyCiv样本报告
查看 SkyCiv 底板设计报告的详细程度和清晰度. 该报告包括所有关键的设计检查, 方程式, 并以清晰易读的格式呈现结果. 完全符合设计标准. 单击下面查看使用 SkyCiv 底板计算器生成的示例报告.
购买基板软件
单独购买基本板设计模块的完整版本，而没有任何其他SkyCiv模块. 这为您提供了底板设计的完整结果, 包括详细报告和更多功能.
