Lors de l'exécution d'un Analyse du spectre de réponse sur un ouvrage, l'une des étapes les plus importantes pour obtenir les résultats souhaités est la définition de la méthode de combinaison modale qui sera utilisée par le logiciel pour obtenir un résultat unique pour le déplacement, réactions, Forces internes, etc… pour chaque degré de liberté parmi les résultats bruts obtenus pour chaque mode de vibration (réponses modales). Ces résultats combinés modaux sont ceux utilisés pour la conception de la structure, c'est pourquoi il est extrêmement important de bien définir la méthode de combinaison modale. Dans cet article, nous plongerons dans certaines méthodes de combinaison modale pour l'analyse du spectre de réponse.
Il est important de mentionner que l'une des étapes les plus importantes lors d'une analyse du spectre de réponse est l'évaluation de la fréquence propre pour chaque mode de vibration et sa contribution de masse, consultez notre documentation sur l'analyse dynamique des fréquences.
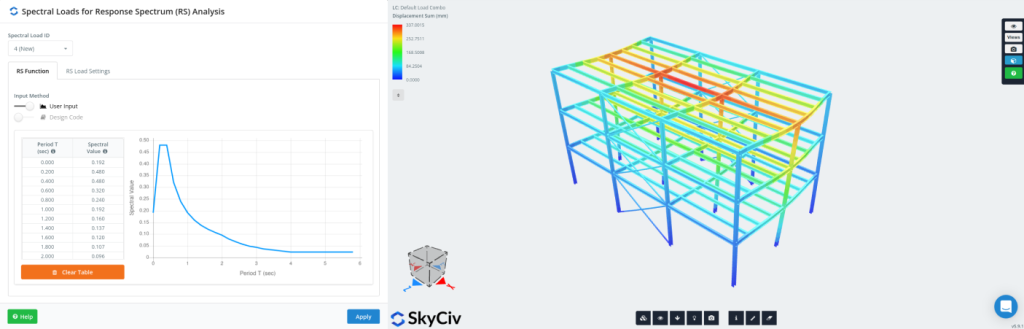
Méthodes de combinaison modale pour l’analyse du spectre de réponse
Certaines des méthodes les plus connues et utilisées pour la combinaison modale sont:
- abdos: Somme absolue
- SRSS: Racine carrée de la somme des carrés
- CQC: Combinaison quadratique complète
En général, valeurs maximales de la réponse totale (\(r_o\)) pour les déplacements, Forces internes, et les réactions sont intéressantes. Comme indiqué précédemment, cette valeur de crête est obtenue en combinant correctement les réponses modales de crête (\(r_{n, le}\))
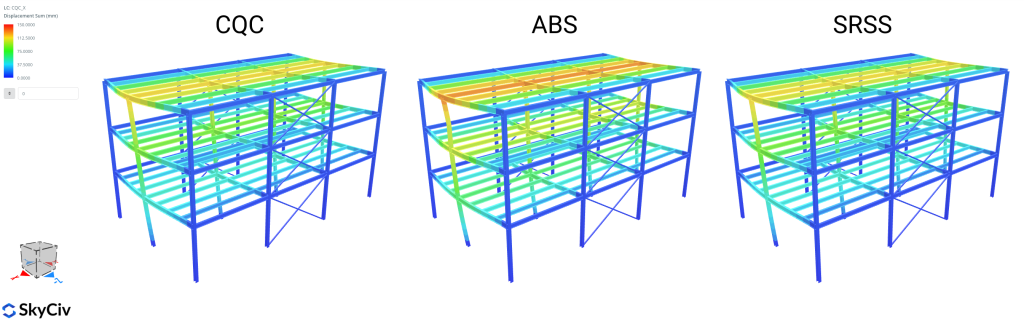
Somme absolue (abdos)
La méthode de combinaison modale Absolute Sum prend la valeur absolue du résultat (déplacement ou force interne) pour chaque mode de vibration et résume toutes ces valeurs absolues. Physiquement, il suppose que toutes les réponses modales de pointe se produisent en même temps. En faisant ça, c'est la méthode la plus conservatrice, car il rend chaque contribution modale positive, et donc, il n'est pas populaire dans les applications de conception structurelle. La formule de calcul de la valeur maximale de la réponse totale est:
\(r_o=\sum_{n=1}^{N} |r_{n,le}|\)
Où,
\(n\) est le \(n^{e}\) mode de vibration considéré dans l'analyse
\(N) est le nombre total de modes de vibration pris en compte dans l'analyse
\(r_o\) est la réponse totale maximale
\(r_{n,le}\) est la réponse modale maximale pour le \(n^{e}\) mode vibration
Racine carrée de la somme des carrés (SRSS)
La méthode de combinaison modale de la racine carrée de la somme des carrés prend la racine carrée de la somme des carrés du résultat pour chaque mode de vibration, fournissant une estimation du pic de la réponse totale. Cette méthode de combinaison modale fournit d'excellentes estimations de réponse pour les structures avec des fréquences naturelles bien séparées, pour les cas où les fréquences propres de la structure ne sont pas bien séparées, cette méthode ne doit pas être utilisée. Officiellement, la réponse totale maximale peut être exprimée comme suit:
\(r_o=\left(\somme_{n=1}^{N} r ^{2}_{n,le}\droite)^{1/2}\)
Où,
\(n\) est le \(n^{e}\) mode de vibration considéré dans l'analyse
\(N) est le nombre total de modes de vibration pris en compte dans l'analyse
\(r_o\) est la réponse totale maximale
\(r_{n,le}\) est la réponse modale maximale pour le \(n^{e}\) mode vibration
Combinaison quadratique complète (CQC)
La méthode de combinaison quadratique complète surmonte la limitation mentionnée pour SRSS lors de la combinaison de réponses modales dans une structure avec des fréquences naturelles étroitement espacées. Dans cette méthode, la réponse totale maximale est obtenue en appliquant la formule suivante:
\(r_o=\left(\somme_{je=1}^{N}\somme_{n=1}^{N} \rho_{in} \cdot r_{io} \cdot r_{non} \droite)^{1/2}\)
Où,
\(n, \; i\) est le \(n^{e}, \; je ^{e}\) mode de vibration considéré dans l'analyse
\(N) est le nombre total de modes de vibration pris en compte dans l'analyse
\(r_o\) est la réponse totale maximale
\(r_{n,le}, \; r_{je,le}\) est la réponse modale maximale pour le \(n^{e}, \; je ^{e}\) mode vibration
\(\rho_{in}\) est le coefficient de corrélation pour les deux modes combinés à chaque étape de sommation
La formule ci-dessus peut être réécrite en deux groupes distincts de sommations, la première étant identique à la méthode de combinaison modale SRSS. La deuxième double sommation inclut toutes les croix (\(i \neq n\)) termes, dont chacun peut être positif ou négatif, cela donne le fait que l'estimation de la réponse totale maximale à l'aide du CQC peut être supérieure ou inférieure à l'estimation fournie par le SRSS :
\(r_o=\left( \somme_{n=1}^{N} r ^{2}_{n,le} + \sous-couche{\somme_{je=1}^{N}\somme_{n=1}^{N}}_{i \neq n} \rho_{in} \cdot r_{io} \cdot r_{non} \droite)^{1/2}\)
Un seul terme dans l'équation pour CQC n'a pas été défini: le coefficient de corrélation. L'une des équations les plus utilisées pour ce coefficient est:
\(\rho_{in} = frac{\xi ^ 2(1+\afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués{in})^ 2}{(1-\afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués{in})^2+4\xi^2\beta_{in}}\)
Où,
\(\afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués{in}\) est le rapport entre les fréquences propres de la \(je ^{e}\) et \(n^{e}\) modes (\(\oméga_i / \omega_n\))
\(\xi\) est le coefficient d'amortissement de la structure
Références
Chopra, A. (2015, juin 4). Dynamique des Structures (4th ed.). Enseignement supérieur Pearson.
Nouveau sur SkyCiv Structural 3D? Inscrivez-vous aujourd'hui GRATUITEMENT!
Développeur de produit
BEng (Civil)



