Didacticiel: How to Solve a Truss Structure using Method of Sections

Dans ce tutoriel, nous explorerons et apprendrons les avantages de l'utilisation de la méthode des sections pour résoudre votre structure en treillis. What are trusses? If you’re unsure about this, visitez notre What is a truss de SkyCiv. La méthode des sections est utilisée pour résoudre rapidement des structures en treillis plus grandes., simple manner. It involves taking a ‘cut’ à travers un certain nombre de membres pour évaluer leurs forces axiales et l'utiliser comme base pour résoudre le reste de la structure en treillis.

La grande chose est, SkyCiv Truss le fait automatiquement pour vous. Modélisez vos propres fermes et le logiciel montrera l'élaboration interactive étape par étape de la méthode des sections!

Regardez le didacticiel vidéo

Exemple de question

Pour notre exemple travaillé, nous allons examiner la question suivante:

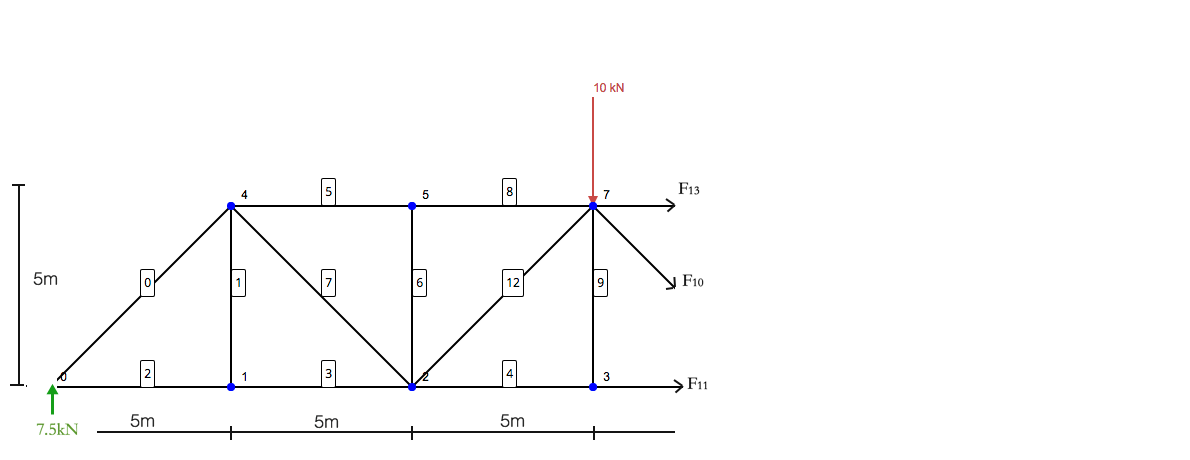
Question: Using the method of sections, determine the forces in members 10, 11, et 13 of the following truss structure:

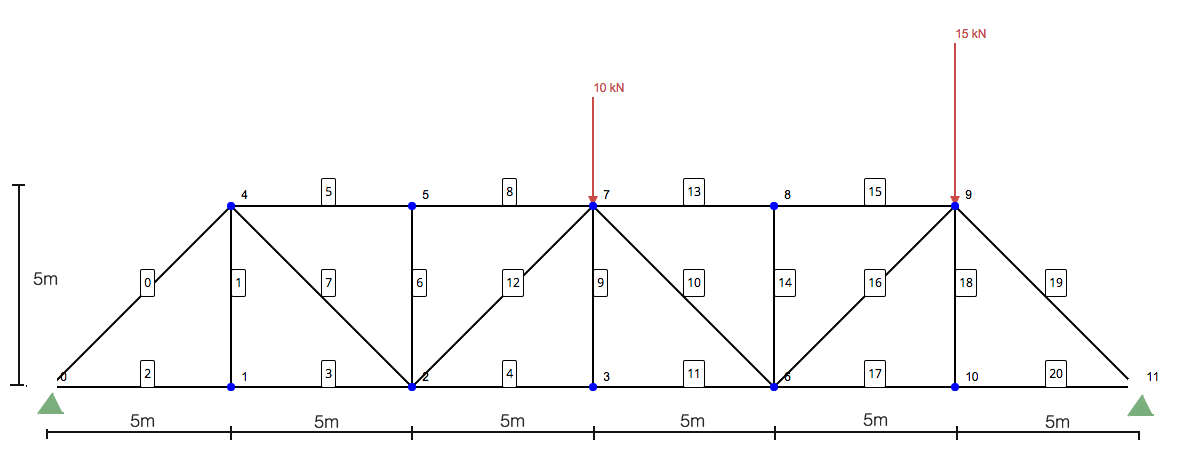
Étape 1: Calculer les réactions aux supports

Comme la plupart des analyses structurelles statiques, nous devons d'abord commencer par localiser et résoudre les réactions aux supports. Cela nous donnera les conditions aux limites dont nous avons besoin pour progresser dans la résolution de la structure en treillis. Simplifier la structure pour n'inclure que les charges et les supports:

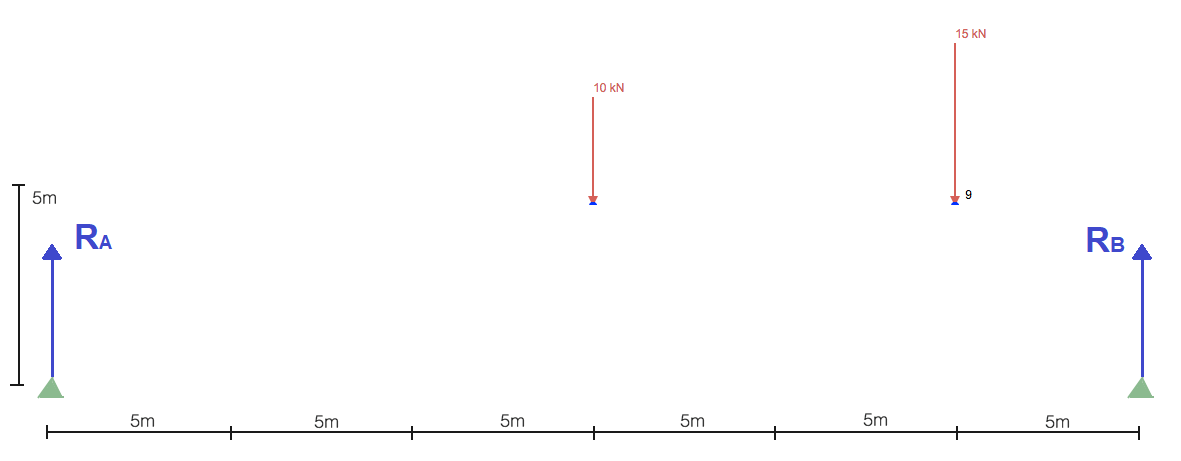
Sans passer trop de temps à calculer les réactions, vous commencez généralement par prendre la somme des moments sur un point. Prendre la somme des moments sur le support gauche nous permet:

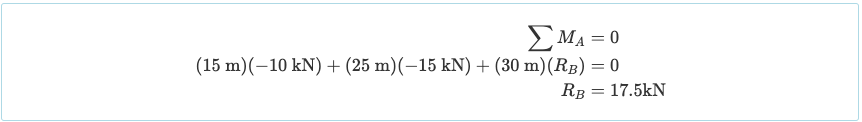
Donc la réaction au bon support (R_B) est 17.5 kN vers le haut. Maintenant, prendre la somme des forces dans y nous donne la réaction R_A comme 7,5 kN dans le sens ascendant:

Étape 2: Faites une coupe le long des membres d'intérêt

Voici la partie la plus importante de la résolution d'une ferme en utilisant la méthode des sections. Il s'agit de faire une part des membres que vous souhaitez résoudre. Cette méthode d'analyse structurelle est extrêmement utile lorsque vous essayez de résoudre certains des membres sans avoir à résoudre toute la structure en utilisant la méthode des joints. Donc, dans notre exemple ici serait notre tranche:

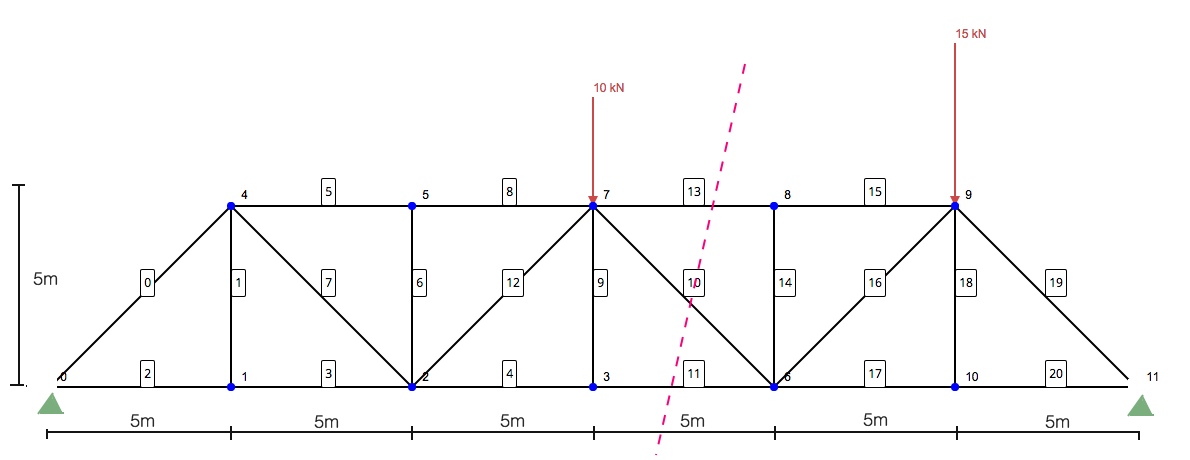
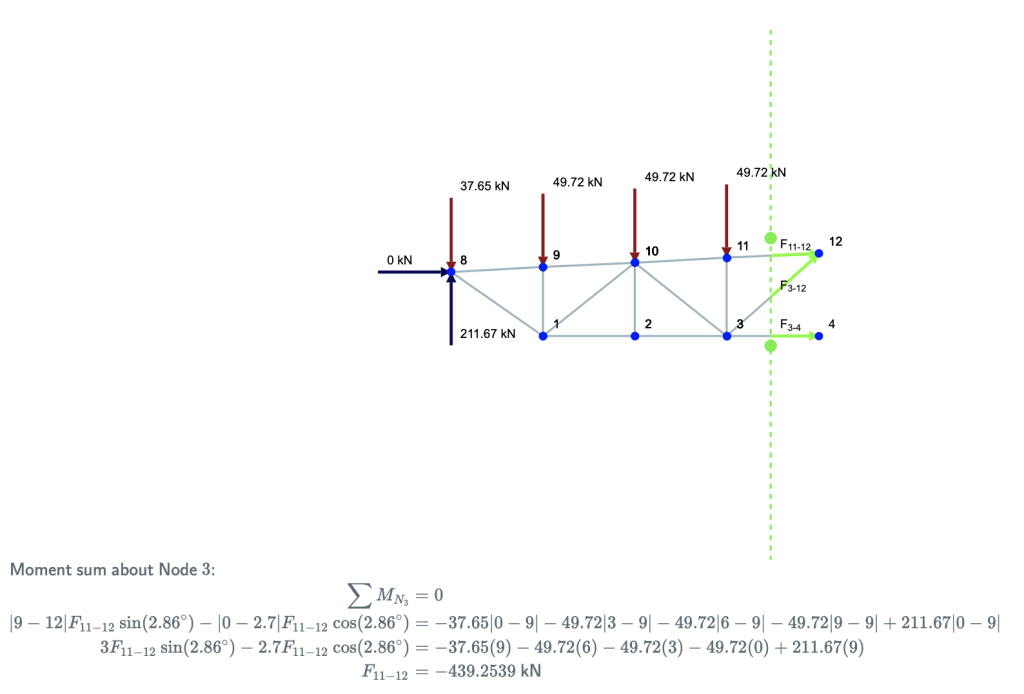
Se concentrer uniquement sur le côté gauche, il vous reste la structure suivante:

Considérez maintenant cette structure comme une structure unique. Les lois de la statique s'appliquent toujours – donc la somme des moments et des forces doit être égale à zéro. Les membres avec des flèches (F₁₃, F₁₀, F₁₁) sont ce qui stabilise la réaction et les forces appliquées à la structure. Notez que la somme des moments est prise sur le nœud 7 – comme cela exclurait les forces des membres 13 et 10 – laissant F₁₁ être isolé.

Utilisation du diagramme de corps libre ci-dessus, on peut obtenir les formules suivantes:

Somme des forces dans la direction y:

[math]
\commencer{aligner}
+\flèche vers le haut text{ } \somme{F_y} &= 0\\
7.5\texte{ kN} – 10 \texte{ kN} – F_{10}sin(45^{\cirque}) &= 0\\
F_{10} &= -3.536 \texte{ kN}
\fin{aligner}
[math]

Somme des moments sur le nœud 7:

[math]
\commencer{aligner}
+\cercleflèchegauche text{ } \somme{M_7} &= 0\\
-(15 \texte{ m})(7.5 \texte{ kN}) + (5 \texte{ m})F_{11} &= 0\\
F_{11} &= 22.5 \texte{ kN}
\fin{aligner}
[math]

Somme des forces dans la direction x:

[math]
\commencer{aligner}
+\flèche droite text{ } \somme{F_x} &= 0\\
F_{13} + F_{11} + F_{10}cos(45^{\cirque}) &= 0\\
F_{13} &= -F_{11} – F_{10}cos(45^{\cirque}) \\
F_{13} &= – (22.5 \texte{ kN}) – (-3.536 \texte{ kN})cos(45^{\cirque}) \\
F_{13} &= -22.5 \texte{ kN} + (3.536 \texte{ kN})cos(45^{\cirque}) \\
F_{13} &= -20 \texte{ kN}
\fin{aligner}
[math]

Solution finale

Nous pouvons utiliser ces résultats pour résoudre les membres restants de la structure en treillis. Nous espérons que cet exemple de calcul de ferme a été utile et n'hésitez pas à commenter avec vos questions ci-dessous. Pour référence, les résultats pour l'ensemble de la structure Truss se trouvent ci-dessous (en utilisant notre Calculatrice de fermes) ce qui est idéal pour vérifier vos réponses!

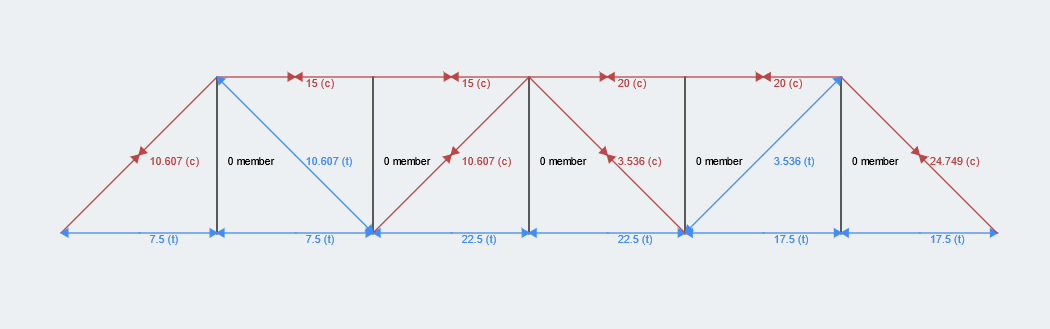
Résumé des étapes

• Commencez toujours par calculer les réactions aux supports
• Faites une part des membres que vous souhaitez résoudre
• Traitez la demi-structure comme sa propre ferme statique
• Résolvez la ferme en prenant la somme des forces = 0
• Prenez le moment d'un nœud de plus d'un membre inconnu

Logiciel SkyCiv Truss

Nous espérons que vous avez trouvé ce tutoriel utile pour vos projets. Visitez notre tutoriels sur les fermes pour plus d'informations utiles sur les fermes et n'oubliez pas de consulter notre guide pour résoudre le treillis par la méthode des joints.

SkyCiv Truss peut calculer la méthode des sections automatiquement pour vous. Ou essayez notre Calculatrice de fermes gratuite qui vous donnera la réponse finale (aucun calcul manuel).

Pour explorer plus de fonctionnalités du logiciel SkyCiv, inscrivez-vous aujourd'hui pour commencer!

Commencez gratuitement