Le moment d'inertie est une propriété géométrique importante utilisée en ingénierie structurelle. Il est directement lié à la résistance en flexion de votre section. En général, un moment d'inertie plus élevé implique une plus grande résistance de la section, ce qui a pour effet de minimiser la flèche lorsque la poutre est soumise à un effort transversal. La désignation “moment d'inertie” est couramment utilisée, mais elle n'est pas strictement adéquate, car cette propriété n'a rien à voir avec l'inertie. Une désignation technique plus approprié est le moment quadratique. Cette désignation décrit plus précisément ce qui est mesuré, qui pourrait être grossièrement décrit comme étant une mesure de la distance entre l'aire d'une section et l'axe neutre.

Table des matières

• Formule du moment d'inertie d'un rectangle
• Sections creuses rectangulaires (HSS)

Formule du moment d'inertie d'un rectangle

La formule générale utilisée pour déterminer le moment d'inertie d'un rectangle est:

[math] JE_{xx}[object Window]{BD ^ 3}{12} , JE_{yy}[object Window]{B^3D}{12} [math]

Où les axes xx et yy désignent respectivement l'axe, ou la direction, considérée.

En ingénierie structurelle, il est courant d'utiliser B pour désigner la largeur d'une section rectangulaire, parallèle à un axe horizontal X.

De manière similaire, D pour désigner la profondeur d'une section rectangulaire, parallèle à un axe vertical Y.

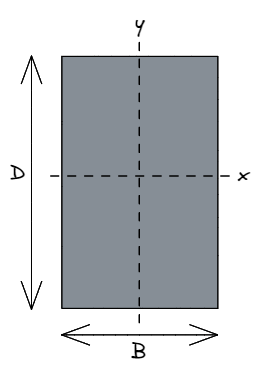
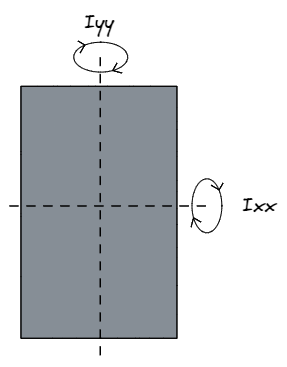
Lorsque les ingénieurs parlent de Ixx ils font référence à la résistance d'une section autour de l'axe des x, c’est-à-dire dans une direction parallèle à D (mm), ou l'axe y. De manière similaire, Iyy réfère à la résistance autour l'axe y, c’est-à-dire dans une direction parallèle à B (mm), ou axe x .

Sections creuses rectangulaires (HSS)

Bien que les ingénieurs pourraient utiliser des sections rectangulaires pleines lors de la conception, cela nécessiterait beaucoup de matière, augmentant ainsi le poids et le coût. Il est bien plus courant d'utiliser des sections creuses (généralement appelées HSS). Ici, nous pouvons utiliser la même équation définie ci-dessus pour un rectangle, toutefois, nous devons soustraire la surface intérieure creuse du rectangle:

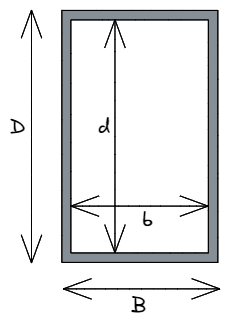
[math] JE_{xx}[object Window]{BD ^ 3}{12} – \dfrac{bd ^ 3}{12} [math]

Dans ce cas, les lettres minuscules b et d désignent les dimensions de la zone creuse à l'intérieur du rectangle que nous devons soustraire des dimensions extérieures, représentées par B et D. La différence entre chaque dimension correspondante fait référence à l'épaisseur du matériau dans cette direction – e.g. B – b = épaisseur totale du matériau parallèle à l'axe x.

Outre les exemples évidents de poids et d'utilisation des matériaux, pourquoi les sections creuses sont-elles souvent décrites comme plus efficaces que leurs équivalents pleins?

Prenons une poutre soumise à une charge verticale. Nous nous attendons à ce que les fibres supérieures du matériau subissent une force de compression, tandis que les fibres inférieures subissent une force de traction. Les fibres situées le long de l'axe neutre de la section (parallèle au centre de gravité de la section) toutefois, ne seront ni en compression ou en tension, d'où la désignation neutre de cet axe.

Également, l' intensité de ces forces de compression ou de traction dépend de la distance par rapport à l'axe neutre – des fibres plus proches de l'axe neutre doivent résister à moins d'effort.

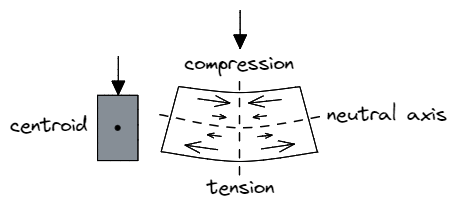
Donc, la partie intérieure d'une section pleine ne résiste qu'à une faible quantité de force tout en occupant une grande surface, alors que les fibres extérieures supportent la majeure partie de la charge! En retirant cette partie intérieure et en rendant la section creuse augmente l'efficacité de la section en termes de poids, de coût, et d'utilisation du matériau.

Conclusion

En résumé, la formule pour déterminer le moment d'inertie d'un rectangle est Ixx=BD³ ⁄ 12, Iyy=B³D ⁄ 12. Pour les sections creuses rectangulaires, la formule devient Ixx=BD³ ⁄ 12 – bd³ ⁄ 12.

Le moment d'inertie est important à la fois pour la force/les contraintes des moments de flexion et pour la déflexion. Cela est évident dans leurs formules, car dans les deux cas, I (Moment d'inertie) se trouve au dénominateur:

Source: Formule de contrainte de flexion

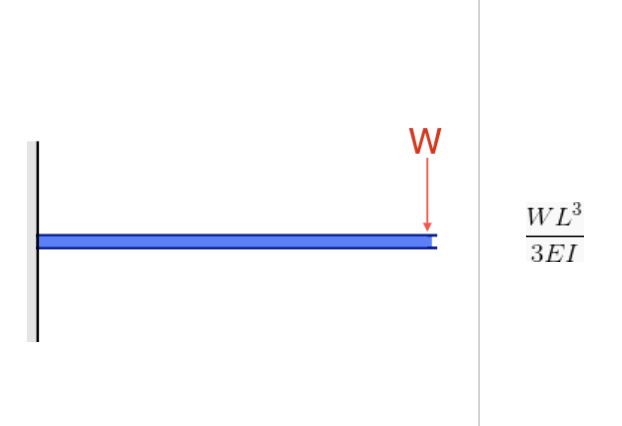
Source: Équation de déviation dans une poutre en porte-à-faux

Calculateur du moment d'inertie d'un cercle

Si vous souhaitez en savoir plus, consultez notre tutoriel sur le moment d'inertie d'un cercle pour comparer les formes de section circulaire et rectangulaire.

Calculateur de moment d'inertie gratuit