Analyse et conception de structures en acier est régi par des normes comme AS 4100:2020, qui utilise la méthode des états limites pour concevoir des éléments de construction en acier. Cette méthode implique le calcul des charges pondérées et des capacités réduites pour tenir compte de la variabilité des conditions de chargement et des propriétés des matériaux.. Pour l’état limite ultime (ULS) concevoir pour être satisfait, la relation suivante doit être vraie:
\(ULS \;Facteur * Charge ≤ Réduction \;Facteur * Capacité)
Ce document décrit la procédure de conception d'un élément en acier conformément à AS 4100 en utilisant le SkyCiv AS 4100:2020 Conception d'élément en acier module.
Contenu
Propriétés matérielles
Fabrication
En Australie, il existe trois formes typiques de fabrication de structures en acier:
- Profilés laminés à chaud: Billette d'acier (blocs) sont chauffés, roulé dans un moulin dans la forme désirée, puis refroidi. Les exemples incluent les poutres/colonnes universelles, Canaux à bride parallèle (PFC) et sections d'angle.
- Sections formées à froid: La billette d'acier est pressée à température ambiante pour lui donner la forme souhaitée. Les exemples incluent les sections creuses rectangulaires (HSS) et sections creuses circulaires (CHS).
- Sections fabriquées: Plusieurs plaques plates laminées à chaud sont soudées ensemble pour former une section en acier. Les exemples incluent les poutres/colonnes soudées.
Nuance d'acier
L'Australie possède de nombreuses qualités d'acier (forces) pouvant être utilisé pour la conception selon AS 4100:2020. Les disponibilités de notes pour différents types de sections sont décrites ci-dessous.
| Noter | BM / toilettes | UB / UC | PFC | ELLE / UA | HSS / SHS | CHS |
|---|---|---|---|---|---|---|
| 250 | NON | NON | NON | NON | NON | OUI |
| 300 | OUI | OUI | OUI | OUI | NON | NON |
| 350 | OUI | OUI | OUI | OUI | OUI | OUI |
| 400 | OUI | NON | NON | NON | NON | NON |
| 450 | NON | NON | NON | NON | OUI | NON |
Limite d'élasticité
La limite d'élasticité d'une section en acier dépend de sa nuance, les qualités supérieures ayant des contraintes d'élasticité plus élevées. La limite d'élasticité des sections laminées à chaud et fabriquées varie en fonction de l'épaisseur de la section. Les sections en acier plus épaisses ont généralement des limites d'élasticité inférieures à celles des sections plus minces de la même nuance..
Les sections formées à froid font exception à cette règle et ont une limite d'élasticité constante pour chaque nuance d'acier., quelle que soit l'épaisseur de la section. Limite d'élasticité et limite d'élasticité de la section (traction) les valeurs de résistance peuvent être calculées à l'aide du tableau 2.1 en AS 4100:2020.
Sélection d'une section dans SkyCiv AS 4100 Conception d'élément en acier
Ce logiciel SkyCiv AS 4100:2020 Conception d'élément en acier l'outil permet aux utilisateurs de sélectionner une section standard dans la base de données SkyCiv ou de concevoir une section entièrement personnalisée. Lorsqu'une section Standard est sélectionnée, les limites d'élasticité des brides et de l'âme sont automatiquement calculées en fonction de la nuance d'acier à l'aide de AS 4100 Le tableau 2.1. Lorsqu'une section personnalisée est sélectionnée, l'utilisateur doit saisir des valeurs pour la limite d'élasticité de la bride et de l'âme. Les sections standard peuvent également être utilisées avec une nuance d'acier personnalisée si l'utilisateur le spécifie..

Capacité des sections
Pliant
Capacité de moment de flexion de section
AS 4100:2020 calcule la capacité de moment de flexion d'une section en acier comme suit:
\(M_s = f_y*Z_e)
Où fY est la limite d'élasticité du matériau, et Ze est le module de section efficace. Le module de section d'une forme est une propriété géométrique qui quantifie la résistance à la flexion d'une forme.. En ingénierie des structures, nous utilisons deux valeurs de module de section, l' élastique (Z) et Plastique (S) module de section. Remarque, les normes de conception dans d'autres régions échangent parfois les symboles pour le module de section élastique et plastique.
Le module de section élastique assume toute la section (vers le bas) reste élastique en flexion, e.g. aucune partie de la section ne dépasse la limite d'élasticité (FY) du matériel. Cela se produit généralement lorsque les fibres extrêmes de la section (haut/bas) atteindre cédant. Le module de section élastique d'une section est calculé comme suit:
\(Z = frac{I}{Y}\)
Où I est le deuxième moment de l'aire et y est le centre de gravité géométrique de la forme.
Le module de section plastique suppose que la section entière atteint la limite d'élasticité du matériau en flexion, ce qui signifie que certaines parties de la section dépasseront la limite d'élasticité et subiront une déformation plastique. Le module de section plastique d'une section est calculé comme suit:
\(S = A_C*y_C + A_T*y_T \)
Où unC et unT sont les zones de chaque côté de l’axe neutre plastique (ANP), Andyc / Yt sont la distance entre le PNA et le centre de gravité de ces zones. Remarque, l'emplacement du PNA est égal à l'emplacement du centre de gravité géométrique pour les formes symétriques mais sera ne pas égal à l'emplacement du centre de gravité géométrique pour les formes asymétriques.
Classement des sections
Certaines formes en acier peuvent avoir des éléments de la forme qui se déforment localement avant d'atteindre leur limite d'élasticité, ce qui signifie que la pleine capacité du module de section élastique/plastique ne peut pas être atteinte. Cela se produit généralement dans des, formes plus fines, qui sont plus sensibles au flambage local. AS 4100 utilise le module de section efficace (Elle) valeur pour tenir compte de la possibilité de flambement local et réduire la capacité de flexion de la section en conséquence. AS 4100 classe les sections en trois catégories:
- Compact: Les sections compactes ne sont pas sensibles au flambement local et peuvent atteindre leur pleine capacité de moment plastique, ce qui signifie que la section entière peut atteindre sa limite d'élasticité en flexion.
- Non compact: Les sections non compactes peuvent atteindre la limite d'élasticité dans les fibres extrêmes de la section (capacité de moment élastique) mais ne peuvent pas atteindre leur capacité de moment plastique avant qu'un flambement local ne se produise.
- Mince: Les sections élancées ne peuvent pas atteindre leur capacité de moment élastique avant qu'un flambement local ne se produise.

Section Élancement
AS 4100 détermine la classification des sections en calculant l'élancement de chaque élément dans une section et en trouvant le “élément critique” qui se déformera en compression en premier. Pour une section en I, les éléments sont décomposés comme indiqué ci-dessous. Les valeurs d'élancement ne sont calculées que pour les éléments remarquables, e.g. éléments qui ne sont pas retenus dans les deux sens. La zone de connexion entre une bride et une âme (montré en blanc ci-dessous) est retenu dans les deux sens et n'est donc pas susceptible de flambage local.
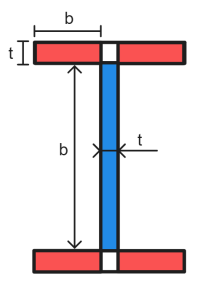
L'élancement d'un élément plat se calcule comme suit:
\(λ_e = frac{b}{t}\sqrt{\frac{f_y}{250}}\)
AS 4100 Le tableau 5.2 contient des valeurs pour les limites de plasticité et d'élancement (λép. & λhé) pour éléments à plaques de compression basés sur la répartition des contraintes, support des bords et contraintes résiduelles. L'élément critique d'une section est l'élément ayant le plus haut λe / λhé rapport. Les valeurs d'élancement de cet élément (λe) sont utilisés pour classer la section entière (appelé λs).
Si λs ≤ λsp la section est compacte. Pour sections compactes, le module de section efficace est calculé comme suit:
\(Z_e = Z_c = min(S,1.5*Z)\)
Où S est le module de section plastique, et Z est le module de section élastique de la section. Le terme Zc est utilisé de manière interchangeable pour le module de section efficace d'une section compacte.
Si λsp ≤ λs ≤ λle sien la section n'est pas compacte. Pour sections non compactes, le module de section efficace est calculé comme suit:
\(Z_e = Z + [(\frac{l_{le sien} – l_{s}}{l_{le sien} – l_{sp}})(Z_c-Z)]\)
Où Zc est le module de section efficace pour une section compacte.
Si λs > λle sien la section est fine. Pour une section élancée avec des éléments plats en compression uniforme, le module de section efficace est calculé comme suit:
\(Z_e = Z(\frac{l_{le sien}}{λ_s})\)
Remarque, le module de section effectif pour les profilés creux circulaires ou les éléments plats avec tension au niveau du bord non soutenu est calculé différemment. Référez-vous à AS 4100 Clause 5.2.5 pour plus d'informations.
Calcul de la capacité de flexion de section dans SkyCiv AS 4100 Conception d'élément en acier
Ce logiciel SkyCiv AS 4100:2020 Conception d'élément en acier l'outil calcule les classifications d'élancement et les capacités de flexion des sections pour la flexion positive et négative autour des deux axes principaux. Les résultats du contrôle de classification d'élancement pour un 230 Les PFC sont détaillés ci-dessous.

Il apparaît que les valeurs d’élancement et le classement des sections sont différents selon le sens de pliage.. En effet, les répartitions des contraintes et les valeurs de support des bords changent en fonction des éléments qui sont en compression ou en tension., ce qui entraîne des valeurs limites d'élancement différentes.
Une fois l’élancement de la section connue, le module calcule la capacité du moment de flexion de la section (afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués) autour de chaque axe principal pour une flexion positive et négative. Pour les formes symétriques (comme les sections en I), cette valeur sera la même dans le sens positif et négatif. Les formes asymétriques auront des capacités de flexion de section différentes dans les directions de flexion positive et négative., comme le 230 PFC montré dans l'exemple ci-dessous.

Tondre
Capacité de cisaillement des sections
AS 4100 considère uniquement l'âme d'une section comme contribuant à sa capacité de cisaillement. D'où la capacité de cisaillement d'une section (Vv) est égale à la capacité de cisaillement de l'âme. Des raidisseurs verticaux peuvent être ajoutés à une section pour augmenter sa capacité de cisaillement si nécessaire. La capacité d'une âme est calculée différemment selon que la répartition des contraintes de cisaillement sur l'âme est uniforme ou non uniforme.. Les distributions de contraintes de cisaillement suivantes sont supposées pour les formes de section standard:
| Forme | Répartition des contraintes de cisaillement | |
|---|---|---|
| Direction Y | Direction Z | |
| Section I | Uniforme | Non uniforme |
| Section en T | Non uniforme | Non uniforme |
| Canal à bride parallèle (PFC) | Uniforme | Non uniforme |
| Angles | Non uniforme | Non uniforme |
| RHS / SHS | Non uniforme | Non uniforme |
| CHS | Uniforme | Uniforme |
Répartition uniforme des contraintes de cisaillement
La capacité de cisaillement d'une section avec une répartition uniforme des contraintes de cisaillement (Vu) est calculé différemment selon l'élancement du panneau web. Pour une toile non fine, la capacité est calculée comme suit:
\(\frac{d_p}{t_w} ≤ frac{82}{\sqrt{\frac{f_y}{250}}}\flèche droite V_u = V_w = 0,6*f_y*A_w)
Remarque pour une section creuse circulaire Vw = 0,36*fY*A.
Quand l'âme de la section est fine, la capacité est calculée comme suit:
\(\frac{d_p}{t_w} > \frac{82}{\sqrt{\frac{f_y}{250}}}\flèche droite V_u = V_b = α_v*V_w)
\(α_v = gauche[\frac{82}{(\frac{d_p}{t_w})\sqrt{\frac{f_y}{250}}}\droite]^2)
Où dp est la profondeur claire du panneau Web (e.g. profondeur hors brides), tw est l'épaisseur du panneau Web, FY est la limite d'élasticité de l'âme et Aw est la surface brute de la section Web. Pas de théw est calculé différemment pour les sections soudées et laminées à chaud. Pour profilés laminés à chaud, Aw prend la profondeur de la bande comme profondeur totale de la section (d). Pour sections soudées, Aw prend uniquement la profondeur d'âme libre entre les brides (dp). Les sections creuses rectangulaires utilisent également dp pour le calcul de Aw.
Répartition non uniforme des contraintes de cisaillement
La capacité de cisaillement d'une section avec une répartition uniforme des contraintes de cisaillement (Vv) est calculé comme suit:
\(V_v = frac{2*V_u}{0.9+\la gauche(\frac{F*_{machine virtuelle}}{F*_{Virginie}}\droite)} ≤ V_u)
Où Vu est la capacité de cisaillement de la section avec une répartition uniforme des contraintes de cisaillement et f*machine virtuelle /F*Virginie est le rapport des contraintes de cisaillement de conception maximales et moyennes dans l'âme.
Calcul de la capacité de cisaillement dans SkyCiv AS 4100 Conception d'élément en acier
Il calcule la capacité de cisaillement d'une section dans les deux axes principaux. Petit axe (Z) la capacité de cisaillement est calculée en utilisant la contribution des brides de section, excluant toute contribution de la section web. Résultats des calculs de capacité de cisaillement pour un 200 UB 22.3 sont détaillés ci-dessous.

Compression
Capacité de compression des sections
AS 4100 calcule la capacité de compression (Ns) d'une section chargée de manière concentrique comme suit:
\(N_s = k_f*A_n*f_y)
Où kF est le facteur de forme de la section, An est l'aire nette de la section transversale (surface brute hors pénétrations/trous) et fY est la limite d'élasticité de la section. Le facteur de forme d'une section représente la mesure dans laquelle une section peut contribuer à sa capacité de compression avant qu'un flambage local ne se produise.. Le facteur de forme est calculé comme suit:
\(k_f = frac{A_e}{A_g}\)
Où ung est la surface brute de la section, et une est le “zone efficace” de la rubrique, e.g. la superficie brute de la section moins tout “inefficace” zones sous compression. Une zone inefficace fait partie de la section qui se déformera avant d'atteindre sa capacité d'élasticité sous compression.. Les surfaces efficaces sont calculées en trouvant le “largeur efficace” de chaque élément de plaque plate dans une section et recalculer la surface de la section à l'aide de ces valeurs de largeur ajustées. La largeur efficace d'un élément plat est calculée comme suit:
\(b_e = bgauche(\frac{l_{hé}}{l_{e}}\droite) ≤b)
Où:
\(λ_e = frac{b}{t}\sqrt{\frac{f_y}{250}}\)
Remarque, la plupart des logiciels de conception utilisent la limite d'élasticité des sections pour les calculs d'élancement des éléments, plutôt que la limite d'élasticité spécifique de l'âme/de la bride. Cela fournira toujours un résultat conservateur. Les valeurs b utilisées pour λe les calculs sont identiques aux dimensions utilisées pour le contrôle de l'élancement des sections de flexion (avec la bride fendue autour de l'âme), mais le b est utilisé pour be le calcul correspond à la largeur totale de la semelle/de l'âme. λhé est tiré de AS 4100 Le tableau 6.2.4, en fonction du support de bord et des contraintes résiduelles de cet élément.
La largeur efficace d'une section creuse circulaire est calculée comme suit:
\(d_e = min(ré_{le}\sqrt{\la gauche(\frac{l_{hé}}{l_{e}}\droite)}, ré_{le}\la gauche(\frac{3*l_{hé}}{l_{e}}\droite)^ 2) ≤ d_{le}\)
Où:
\(λ_e = gauche(\frac{faire}{t}\droite)\la gauche(\frac{f_y}{250}\droite)\)
Calcul de la capacité de compression de section dans SkyCiv AS 4100 Conception d'élément en acier
Le facteur de forme et la capacité de compression de section (Ns) sont calculés pour les sections australiennes standard et les sections personnalisées définies par l'utilisateur. Résultats des calculs de capacité de compression de section pour un 610UB 125 sont détaillés ci-dessous.

Tension
Capacité de tension des sections
AS 4100 calcule la capacité d'un élément de tension (NT) comme suit:
\(N_t = min(UNE_{g}*F_{Y}\; ,\; 0.85*k_t*A_n*f_u)\)
Où ung est la surface brute de la section, An est l'aire nette de la section transversale (surface brute hors pénétrations/trous), FY est la limite d'élasticité de la section, Fu est la traction (ultime) résistance de la section et kt est le facteur de correction de la répartition de la force de traction. Le Kt utilisé dans la conception varie en fonction de la forme de la section et du type de connexion. Les connexions qui assurent une répartition uniforme des forces donnent lieu à un kt facteur de 1.0, les connexions avec une répartition inégale des forces donnent lieu à un kt facteur entre 0.75-1.0.
Calcul de la capacité de tension dans SkyCiv AS 4100 Conception d'élément en acier
Notre outil permet aux utilisateurs de préciser la section kt valeur pour utilisé dans la conception. Un k inférieurt Cette valeur entraînera une capacité de tension de section inférieure. Le SkyCiv AS 4100 Le calculateur de conception de barres suppose qu'aucun trou significatif n'est présent dans la section., donc An est pris égal à Ag. Résultats des calculs de capacité de tension de section pour un 610UB 125 sont détaillés ci-dessous.

Capacité des membres
Pliant
Capacité de moment de flexion des membres
La capacité de moment de flexion d'un élément en acier peut ne pas toujours être régie par la capacité de moment de flexion de la section. (Ms). En effet, les membres peuvent échouer par une autre méthode avant que la capacité de la section ne soit atteinte.. Le déversement par torsion latérale est une méthode de rupture courante pour les éléments en acier longs/non retenus., ce qui se produit lorsque la section s'éloigne de son axe majeur (vers son petit axe) réduisant sa capacité de moment dans le sens de la flexion.

AS 4100 contient des conseils sur le calcul de la capacité nominale des membres (Mb), qui prend en compte la capacité de section d'un élément en acier (Ms) pour tenir compte de l'impact de l'élancement des membres et des conditions de retenue.
Membres avec retenue latérale complète
Bride critique
La semelle critique d'une section transversale est la semelle qui fléchirait le plus lors du flambage., entraînant finalement une rupture par déversement par torsion. Il s'agit généralement de la bride de compression d'un élément. Les emplacements critiques des brides pour les sections standard soumises à une charge verticale sont indiqués ci-dessous..

Retenue latérale complète
Les éléments plus courts avec une rigidité rotationnelle/latérale élevée sont moins susceptibles de tourner hors du plan sous charge, réduire la probabilité de rupture par déversement par torsion. Si un membre est suffisamment court/rigide, il pourra atteindre sa capacité de moment de section (Ms) avant qu'une autre méthode de défaillance ne se produise. Les membres qui satisfont à cette condition sont réputés avoir “Retenue latérale complète”.
\(Plein \; Latéral \; Rigidité en rotation \; \flèche droite M_b = M_s)
AS 4100 Clause 5.3.2 fournit des conseils sur le calcul de la limite de retenue latérale complète pour un membre. Sections creuses circulaires (CHS) et sections creuses carrées (SHS) ne sont pas sensibles au déversement par torsion, car ils ont une rigidité latérale/torsionnelle élevée et des capacités de moment de section égales autour des deux axes. Par conséquent, ces sections sont généralement supposées assurer une retenue latérale totale, quelle que soit la longueur de l'élément..
Retenue latérale continue
Les éléments qui ont une retenue continue sur la semelle critique sur toute leur longueur sont considérés comme ayant “Retenue latérale continue”. Le maintien latéral continu est considéré comme équivalent au maintien latéral complet pour le calcul de la capacité de flexion des éléments. (Mb).
Membres sans retenue latérale complète
La capacité de moment de flexion d'un élément qui n'atteint pas une retenue latérale complète est calculée comme suit:
\(M_b = α_m*α_s*M_s ≤ M_s)
Où αm est le facteur de modification du moment et αs est le facteur de réduction de l'élancement. AS 4100 Clause 5.6 décrit la procédure de calcul de αm et αs.
Capacité de flexion des membres de l'axe mineur
La capacité de flexion d'un élément plié autour de son petit axe (Mb) est égale à la capacité de la section du petit axe (Ms) autour de cet axe. La capacité de la section de l'axe mineur reflète la capacité minimale que la section peut atteindre autour de n'importe quel axe., par conséquent, le membre ne peut pas tourner à partir de cet axe vers une orientation moins favorable.
Calcul de la capacité de flexion des membres dans SkyCiv AS 4100 Conception d'élément en acier
Cet outil effectue des contrôles complets de retenue latérale et calcule les capacités de moment de flexion des éléments autour des deux axes principaux pour la flexion positive et négative.. Les utilisateurs ont également la possibilité de sélectionner “Retenue latérale continue” pour contourner la vérification du maintien latéral complet. Les résultats des calculs de capacité de flexion des éléments pour un 200UB22.3 de 3 m de long sont détaillés ci-dessous..

Remarque, cette calculatrice suppose βs = -1.0 dans tous les calculs.
Compression
Capacité de compression des membres
La capacité de compression axiale d'un élément est également affectée par sa longueur, conditions de rigidité latérale et de retenue. Effréné, les éléments plus longs sont susceptibles de se rompre en raison du flambement par flexion avant la section (squash) la capacité est atteinte. AS 4100 contient des conseils sur le calcul de la capacité nominale des membres (Nc), qui prend en compte la capacité de la section de compression (Ns) pour tenir compte de l'impact de l'élancement des membres et des conditions de retenue.
\(N_c = α_c*N_s ≤ N_s\)
Où αc est le facteur de réduction de l'élancement de la barre. Clause 6.3.3 d'AS 4100 fournit des conseils sur le calcul de αc. La capacité de compression des barres doit être vérifiée autour des deux axes pour trouver la valeur déterminante.
\(α_c = ξ\left[1 – \sqrt{ 1 – \la gauche( \frac{ 90}{etc.} \droite)^ 2} \droite]\)
\(\xi = \frac{ \la gauche( \frac{ \lambda }{90} \droite)^ 2 + 1 + \et }{2 \la gauche( \frac{ \lambda }{90} \droite)^ 2}\)
\(\lambda = \lambda_n + α_aα_b\)
\(h = 0.00326(\lambda – 13.5) \gq 0\)
\(\alpha_a = \frac{2100(\lambda_n – 13.5)}{\lambda_n^2 – 15.3\lambda_n + 2050}\)
\(\lambda_n = gauche( \frac{le}{r} \droite) \sqrt{k_f} \sqrt{\frac{f_y}{250}}\)
Où (Le) et r sont la longueur effective et le rayon de giration pour l'axe de flambement concerné. uneb la section membre est-elle constante, qui est déterminé à l'aide de AS 4100 Le tableau 6.3.3. La logique adoptée par ce module de calcul pour l'affectation de αb est décrit ci-dessous:
| kF | Stress résiduel | Type de section / Forme | tF ≤ 40? | uneB |
|---|---|---|---|---|
| < 1 | HEURE | Section I | Oui | 0 |
| Non | 1.0 | |||
| Autre | – | 1.0 | ||
| Matériel | Section I | Oui | 0.5 | |
| Non | 1.0 | |||
| HSS / SHS | – | 0 | ||
| Autre | – | 1.0 | ||
| FC | N'importe lequel | – | -0.5 | |
| = 1 | HEURE | Section I | Oui | 0 |
| Non | 1.0 | |||
| Autre | – | 0.5 | ||
| Matériel | Section I | – | 0 | |
| HSS / SHS | – | 0 | ||
| Autre | – | 0.5 | ||
| FC | N'importe lequel | – | -0.5 |
Remarque:
– Les sections creuses sont supposées ne pas être relâchées pour le calcul de la constante de section des éléments. (uneb).
– Les sections WB/WC et toutes les sections personnalisées sont supposées être fabriquées à partir de plaques oxycoupées lors du calcul de la constante de section des éléments. (uneb).
Calcul de la capacité de compression des membres dans SkyCiv AS 4100 Conception d'élément en acier
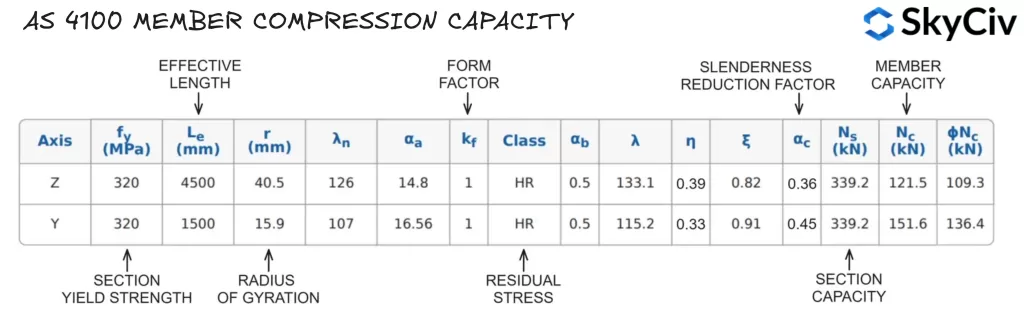
L'outil calcule la capacité de compression des éléments autour des deux axes principaux en fonction des longueurs de retenue et des facteurs de longueur effective spécifiés par l'utilisateur.. Résultats des calculs de capacité de compression des éléments pour un 200UB22.3 avec une longueur non retenue de 4 500 mm et 1 500 mm dans les axes Z et Y. (respectivement) sont détaillés ci-dessous.
Logiciel de conception structurelle SkyCiv
SkyCiv propose une large gamme de logiciels d'analyse structurelle et de conception technique, y compris:
- AS / NZS 1664 Conception en aluminium
- AS / NZS 4600 Conception des pannes
- AS 3600 Conception de murs de cisaillement en béton
- AS 2870 Dalle résidentielle sur conception de niveau
- AS / NZS 1576 Conception d'échafaudages
- AS 4055 Calculateur de charges de vent
Développeur de logiciels | Ingénieur en structure
BEng (Civil), DipEng (Logiciel)



