Un exemple pleinement travaillé de NBCC 2015 calculs de charge de neige
L'accumulation de neige sur les structures peut être très dangereuse pour les membres du toit ou d'autres éléments structurels exposés. Ce logiciel Code national du bâtiment du Canada (2015) Division B – Section 4.1.6 fournit un calcul détaillé des charges de neige et des charges de pluie associées. Utilisation de ce guide, nous montrerons comment calculer les charges de neige à l'aide d'un exemple structurel 3D (S3D) modèle d'entrepôt, comme indiqué ci-dessous:
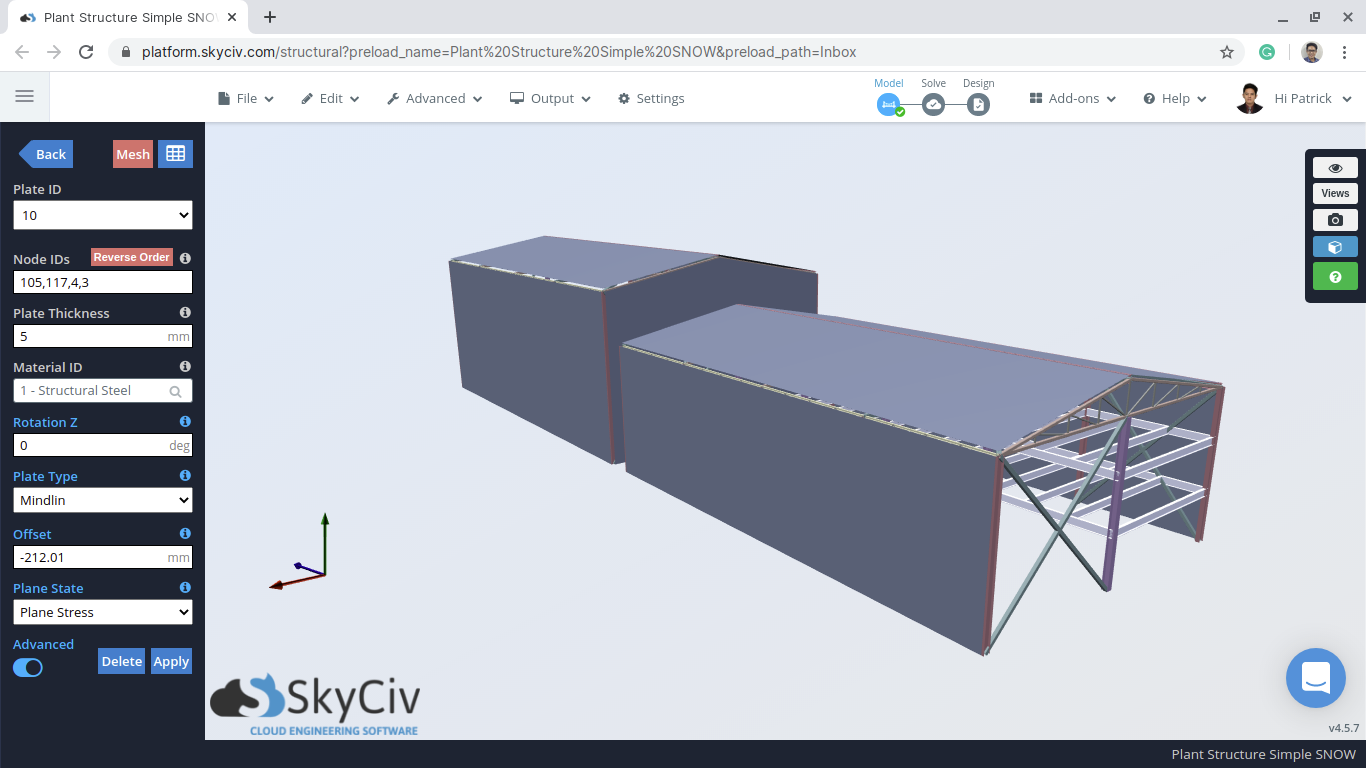
Figure 1: Exemple de modèle d'entrepôt S3D
Figure 2: Exemple d'emplacement de site à l'aide de Google Maps (à titre d'illustration uniquement).
Le tableau 1: Données du bâtiment nécessaires pour notre calcul de la charge de neige.
| Localisation | Ogden, Calgary, Alberta (à titre d'illustration uniquement) |
| Usage | Entrepôt ou stockage de matériaux |
| Dimensions | 19.508 m x 31.70 m pour chaque structure Hauteur d'avant-toit d'un petit bâtiment 9.144 m Hauteur de l'apex du petit bâtiment 11.941 m La différence de toit supérieur et inférieur est 3.50 m Angle d'inclinaison du toit 16° |
| Détails supplémentaires | Le toit a une surface glissante L'écart entre les structures est 2.30 m |
De la table 1, la charge de neige spécifiée, \(S ), peut être calculé à l'aide de la formule:
\(S = {I}_{s}[{S}_{s}{C}_{b}{C}_{w}{C}_{s}{C}_{a} +{S}_{r}]\) (1)
Où:
\({I}_{s}\) = facteur d'importance pour la charge de neige, Tableau 4.1.6.2-A
\({S}_{s}\) = 1-charge de neige au sol en 50 ans, kPa, Sous-section 1.1.3
\({C}_{b}\) = facteur de charge de base pour la neige du toit, 4.1.6.2 (2)
\({C}_{w}\) = basé sur le facteur d'exposition au vent, 4.1.6.2 (3) et (4)
\({C}_{s}\) = facteur de pente, 4.1.6.2 (5), (6), et (7)
\({C}_{a}\) = facteur d'accumulation, 4.1.6.2 (8)
\({S}_{r}\) = Charge de pluie associée 1 en 50 ans, kPa, Sous-section 1.1.3, mais pas supérieur à \({S}_{s}{C}_{b}{C}_{w}{C}_{s}{C}_{a}\)
Chaque paramètre sera examiné individuellement dans les sections suivantes. Les cas de charge de neige suivants seront calculés: charge de neige équilibrée et déséquilibrée sur chaque toit (vent normal à la crête), ainsi que la dérive générée sur le toit inférieur compte tenu de l'accumulation de glissement.
Facteur d'importance, \({I}_{s}\)
La première chose qui est déterminée est le facteur d'importance, \({I}_{s}\), qui se trouve en utilisant Tableau 4.1.6.2-A comme référencé. Puisque la structure est un bâtiment de stockage qui a un faible impact direct sur la vie humaine en cas de panne, la catégorie d'importance est Faible. De plus, le calcul sera dans l'état limite ultime (ULS). Donc de Tableau 4.1.6.2-A, \({I}_{s}\) est égal à 0.80.
| Catégorie d'importance | Facteur d'importance, \({I}_{s}\) | |
|---|---|---|
| ULS | SLS | |
| Faible | 0.8 | 0.9 |
| Ordinaire | 1.0 | 0.9 |
| Haute | 1.15 | 0.9 |
| Après la catastrophe | 1.25 | 0.9 |
Charge de neige au sol, \({S}_{s}\), et charge de pluie associée, \(({S}_{r})\)
La charge de neige au sol, \({S}_{s}\), et charge de pluie associée, \(({S}_{r})\), les valeurs sont tabulées dans Annexe C, Division B du NBCC 2015 selon l'emplacement et la province. Dans cet exemple, le correspondant \({S}_{s}\) et \(({S}_{r})\) in Calgary, Alberta est égal à 1.10 kPa et 0.1 kPa, respectivement.
Avoir du mal à rechercher la neige au sol et la charge de pluie associée pour le NBCC 2015? Essayez l' Outil générateur de charge libre SkyCiv pour accélérer votre recherche et obtenir les \({S}_{s}\) et \({S}_{r}\) en fonction de l'emplacement de votre structure.
Facteur d'exposition au vent, \({C}_{w}\)
Pour le facteur d'exposition au vent, \({C}_{w}\), il doit être autorisé à être égal à 1.0 basé sur 4.1.6.2 (3). Ce facteur peut encore être réduit tant que les conditions 4.1.6.2 (4) est satisfait. Dans cet exemple, \({C}_{w}\) doit être égal à 1.0 puisque l'emplacement n'est pas un terrain dégagé qui expose complètement la structure au vent.
Facteur de charge de neige de base du toit, \({C}_{b}\)
Le facteur de charge de base de la neige sur le toit, \({C}_{b}\), peut être calculé à l'aide des formules suivantes, comme référencé dans 4.1.6.2 (2):
\({C}_{b} = 0.8\) (2) pour \({l}_{c} ≤ (70/{{C}_{w}}^{2})\) et
\({C}_{b} = (1/{C}_{w}) [1 – (1 – 0.8{C}_{w})exp(-0.01({l}_{c}{{C}_{w}}^{2} – 70))] \) (3) pour \({l}_{c} > (70/{{C}_{w}}^{2})\)
Où:
\({l}_{c}\) = longueur caractéristique du toit supérieur ou inférieur définie comme: \(2w -{w}^{2}/[object Window])
\([object Window]) = plus grande dimension en plan du toit
\(w ) = plus petite dimension en plan du toit
Dans cet exemple,\([object Window]) et \(w ) est égal à 31.7 m et 19.51 m, respectivement, donc, \({l}_{c}\) est égal à 27.01. Puisque \({l}_{c}\) est inférieur à \((70/{1.0}^{2})\), le facteur de charge de neige de base du toit, \({C}_{b}\), est égal à 0.8.
Facteur de pente, \({C}_{s}\)
Le calcul du facteur de pente est \({C}_{s}\) détaillé dans 4.1.6.2 (5), (6), et (7) est montré ci-dessous.
Pour toiture glissante dégagée:
\({C}_{s} = 1.0\) pour \(α ≤ 15°\)
\({C}_{s} = 0\) pour \(une > 60°\)
\({C}_{s} = (60° – une)/45°\) pour \(15° < α ≤ 60°\)
Pour les autres cas:
\({C}_{s} = 1.0\) pour \(α ≤ 30°\)
\({C}_{s} = 0\) pour \(une > 70°\)
\({C}_{s} = (70° – une)/40°\) pour \(30° < α ≤ 70°\)
Poids spécifique de la neige, \(γ\)
Le poids spécifique de la neige est spécifié dans 4.1.6.13 et doit être considéré comme:
\(γ = 0.43{S}_{s} + 2.2 kN /{m}^{3} ≤ 4,0 kN /{m}^{3}\) (4)
Dans cet exemple, \(γ\) est égal à \(2.673 kN /{m}^{3}\).
Facteur d'accumulation, \({C}_{a}\)
Facteur d'accumulation, \({C}_{a}\), w w 4.1.6.2 (8). w.
Charge de neige spécifiée, \(S )
Dans cette section, la charge de neige spécifiée, \(S ), sera calculé pour les cas équilibré et dérivé.
Boîtier équilibré / non dérivé
Pour le boîtier équilibré / non dérivé, l' facteur d'accumulation \({C}_{a}\) est égal à 1.0. De plus, w \(α\) est \(16°\) et la surface du toit est supposée être non obstruée et glissante, le facteur de pente, \({C}_{s}\), pour notre exemple est égal à 0.978. Utiliser l'équation (1), la charge de neige spécifiée, \(S ), pour le cas équilibré / non dérivé est:
\(S = 0.8((1.10)(0.8)(1.0)(0.978)(1.0) +0.1)\) = 0.769 kPa
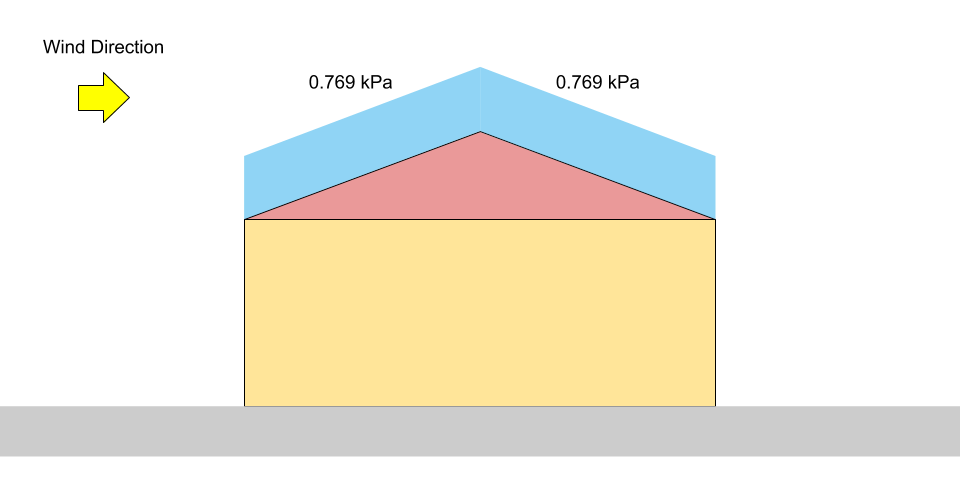
Figure 3: Diagramme de charge pour une charge de neige équilibrée sur un toit à pignon.
Boîtier déséquilibré / dérivé
Vent agissant normalement à la crête
Puisque les structures ont des toits à pignon, la charge de neige déséquilibrée (vent agissant normalement à la crête) facteur d'accumulation \({C}_{a}\) est trouvé en utilisant 4.1.6.9:
\({C}_{a, au vent} = 0\)
\({C}_{a, sous le vent} = 0.25 +α / 20 ) pour \(15° ≤ α ≤ 20°\)
\({C}_{a, sous le vent} = 1.25\) pour \(20° < α ≤ 90°\)
Parce que les deux structures ont un angle d'inclinaison du toit égal à 16 °, les facteurs d'accumulation \({C}_{a, au vent}\) et \({C}_{a, sous le vent}\) sont égaux à 0 et 1.05, respectivement. De plus, w \(α\) est \(16°\) et la surface du toit est supposée être non obstruée et glissante, le facteur de pente, \({C}_{s}\), pour notre exemple est égal à 0.978.
Dans le cas déséquilibré / dérivé normal à la crête, \({C}_{a}\) doit être calculé en fonction de 4.1.6.9 pour une caisse de toit à pignon. D'après le calcul ci-dessus, \({C}_{a, au vent} = 0\) et \({C}_{a, sous le vent} = 1.05\). Donc, les charges de neige spécifiées pour chaque côté sont:
\({S}_{au vent} = 0.8((1.10)(0.8)(1.0)(0.978)(0) +0.1)\) = 0.08 kPa = \({p}_{1}\)
\({S}_{sous le vent} = 0.8((1.10)(0.8)(1.0)(0.978)(1.05) +0.1)\) = 0.803 kPa = \({p}_{2}\)
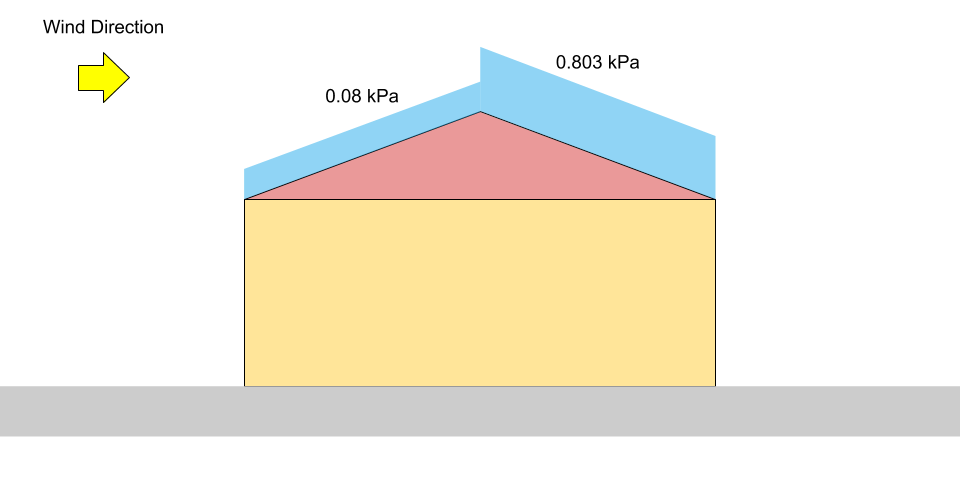
Figure 4: Diagramme de charge pour une charge de neige déséquilibrée sur un toit à pignon (Pas à l'échelle).
Vent agissant parallèlement à la crête – Cas I – Vent du toit supérieur au toit inférieur
Lorsque le vent agit parallèlement à la crête, une traînée de neige se développera très probablement sur le toit inférieur. w facteur d'accumulation \({C}_{a}\), les formules suivantes de 4.1.6.2 (8) par exemple:
\({C}_{a} ={C}_{A0} – ({C}_{A0} – 1)(X/{X}_{d})\) pour \(0 ≤ x ≤ {X}_{d}\)
\({C}_{a} = 1.0\) pour \(X > {X}_{d}\)
Où:
\({C}_{A0}\) = valeur de crête de \({C}_{A0}\) à x = 0
\(X) = distance de la marche du toit
\({X}_{d}\) = longueur de la dérive comme indiqué sur la figure 3 ci-dessous
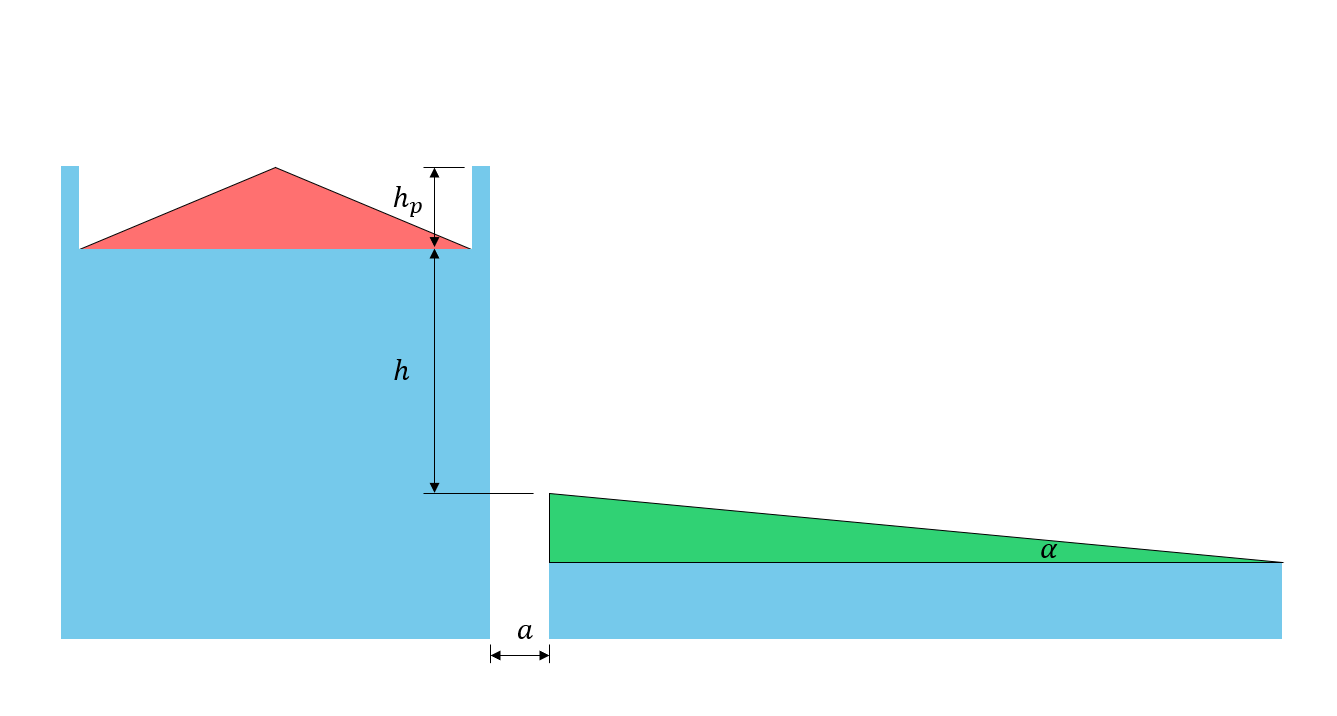
Figure 5: Illustration des paramètres de dimension du toit
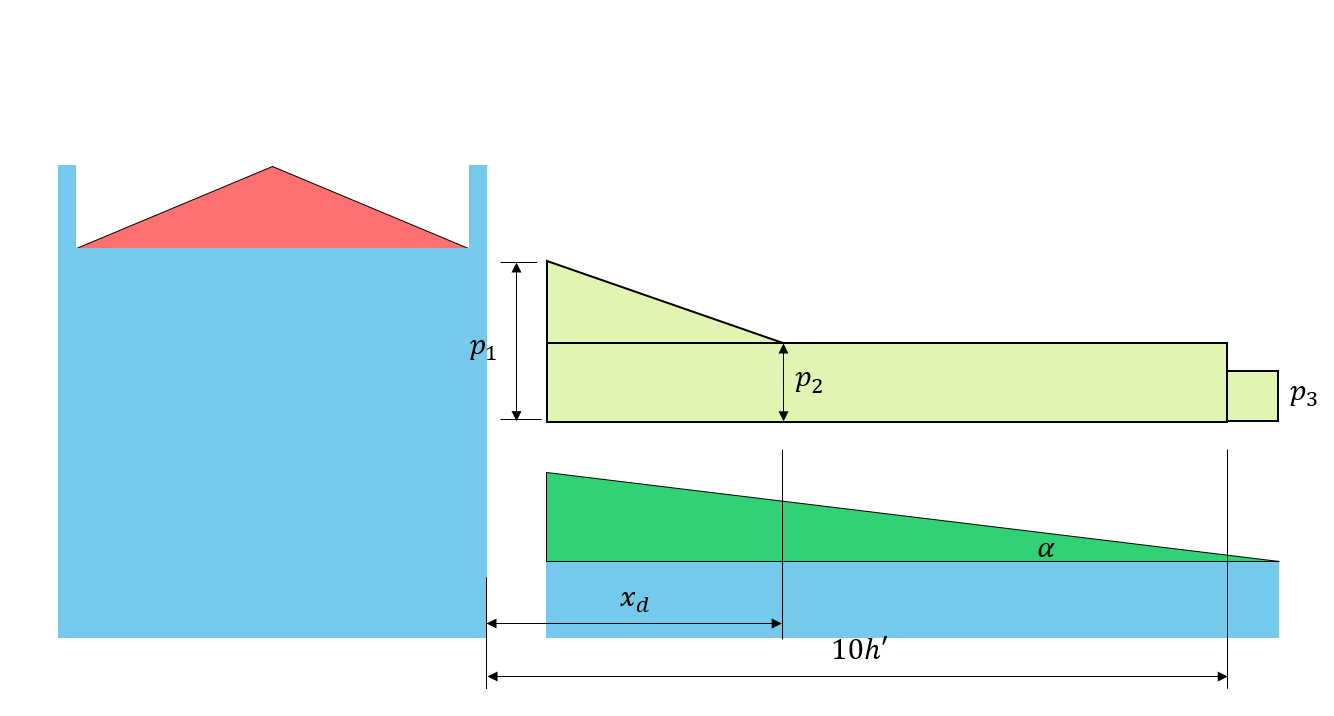
Figure 6: Charge de dérive correspondante sur le toit inférieur en fonction de Graphique 4.1.6.5-A.
\({C}_{A0}\) et \({X}_{d}\) peut être calculé à l'aide des formules suivantes:
\({C}_{A0} = frac{βγh}{{C}_{b}{S}_{s}}\) ou \({C}_{A0} = frac{F}{{C}_{b}}\) (5), celui qui est le moins élevé
\({X}_{d} = 5 \frac{{C}_{b}{S}_{s}}{c}({C}_{A0} – 1)\) (6)
\(F = 0,35β sqrt{\frac{c({l}_{cs} – 5{{h}_{p}}^{«})}{{S}_{s}}} +{C}_{b}\) mais \(F ≤ 5\) pour \({C}_{ws} = 1.0\) (7)
\({h}^{«} = h – \frac{{C}_{b}{C}_{w}{S}_{s}}{c}\) (8)
\({{h}_{p}}^{«} ={h}_{p} – \frac{0.8{S}_{s}}{c}\) mais \(0 ≤ {{h}_{p}}^{«} ≤ \frac{{l}_{cs}}{5}\) (9)
Où:
\({h}_{p}\) = hauteur du parapet sur le toit supérieur (0 dans ce cas puisqu'il n'y a pas de parapet)
\(h ) = différence de hauteur entre le niveau supérieur et inférieur du toit
\({C}_{ws}\) = valeur de \({C}_{w}\) applicable à la source de dérive
\({l}_{cs}\) = longueur caractéristique de la zone source définie comme: \(2{w}_{s} -{{w}_{s}}^{2}/{l}_{s}\)
\({l}_{s}\) = plus grande dimension en plan de la zone source comme indiqué sur la figure 7 et 8, indiquée ci-dessous
\({w}_{s}\) = dimension de plan plus petite de la zone source comme indiqué sur la figure 7 et 8, indiquée ci-dessous
\(β\) = 1.0 pour le cas I, et 0.67 pour les cas II et III.
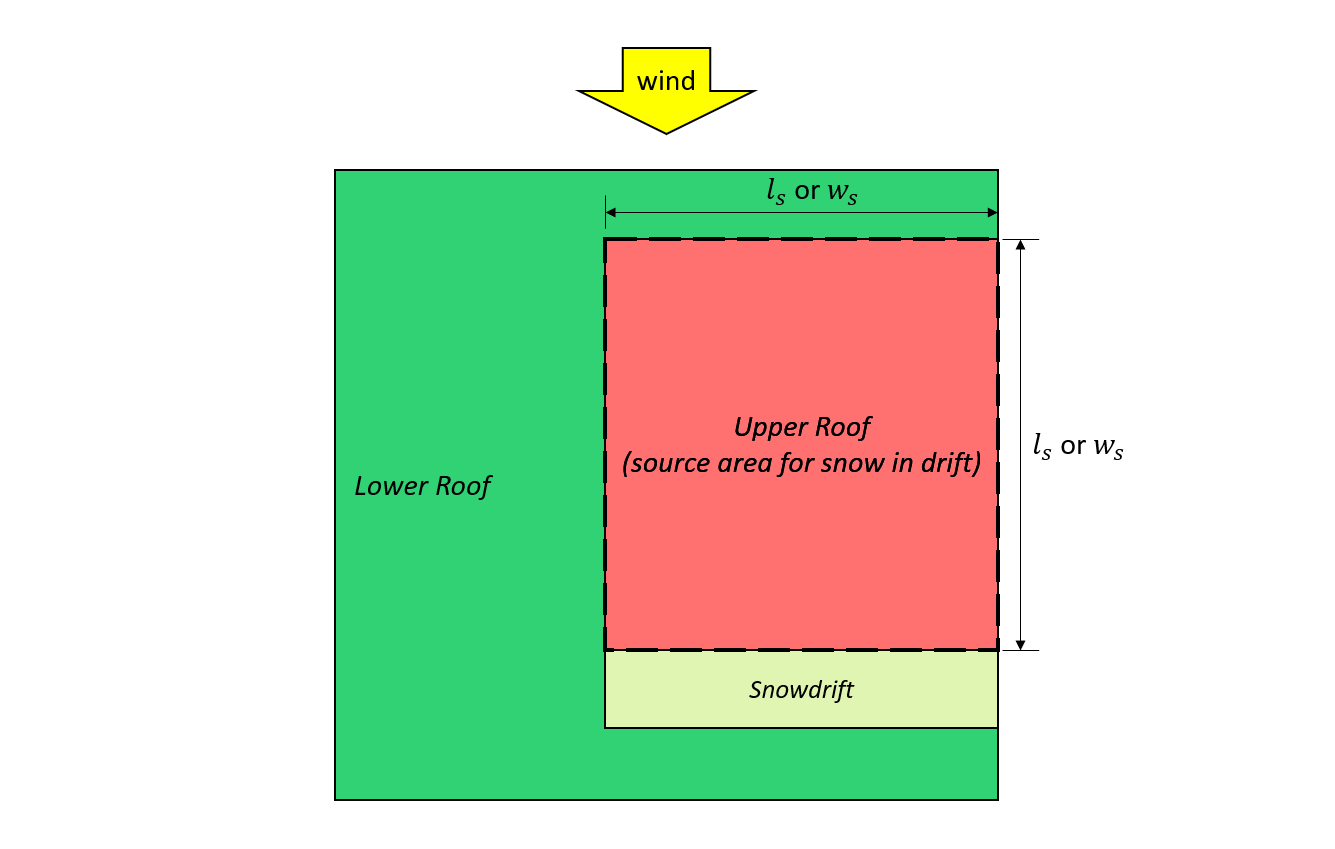
Figure 7: Cas I – neige formée par le vent venant du toit supérieur basé sur Graphique 4.1.6.5-B.
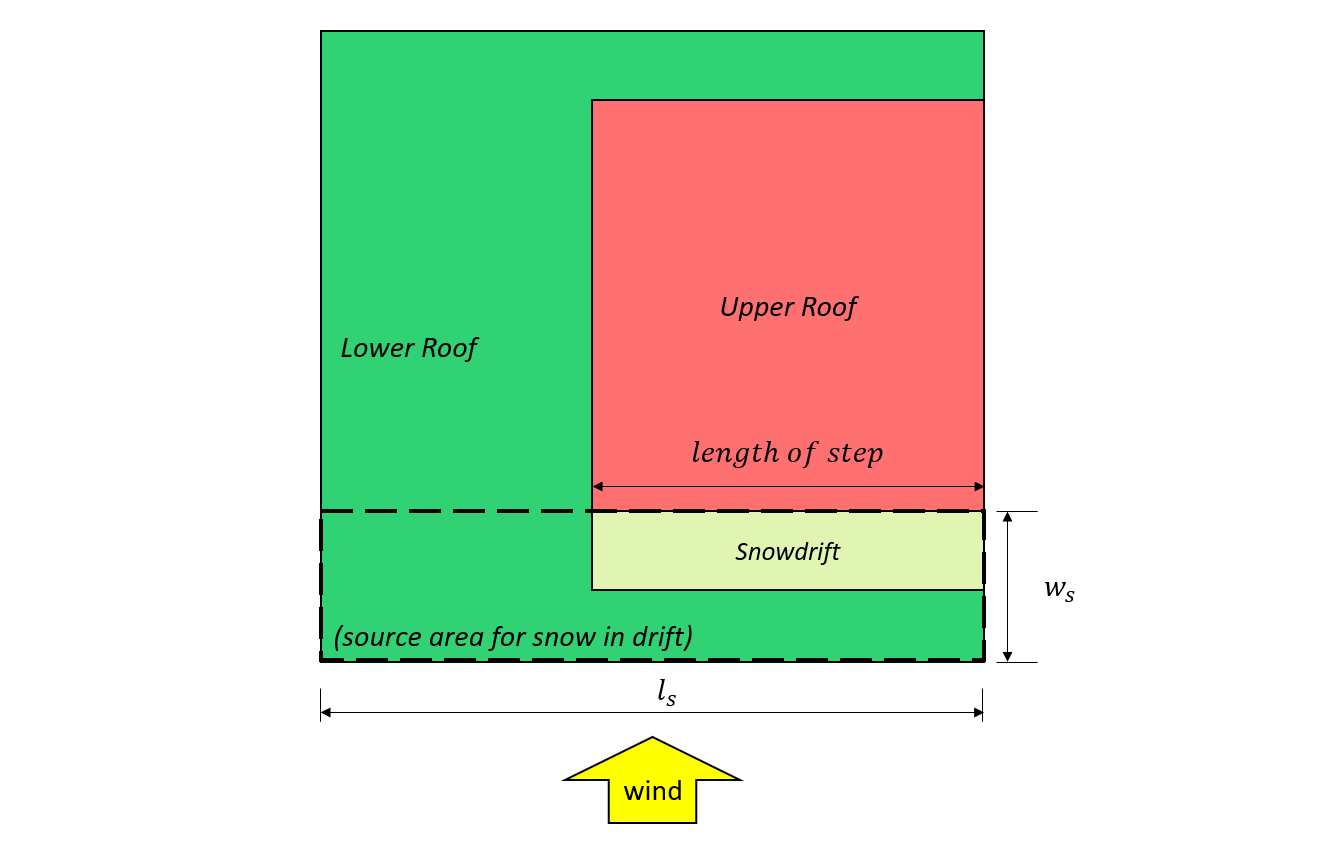
Figure 8: Cas II – neige formée par le vent provenant du toit inférieur basé sur Graphique 4.1.6.5-B.
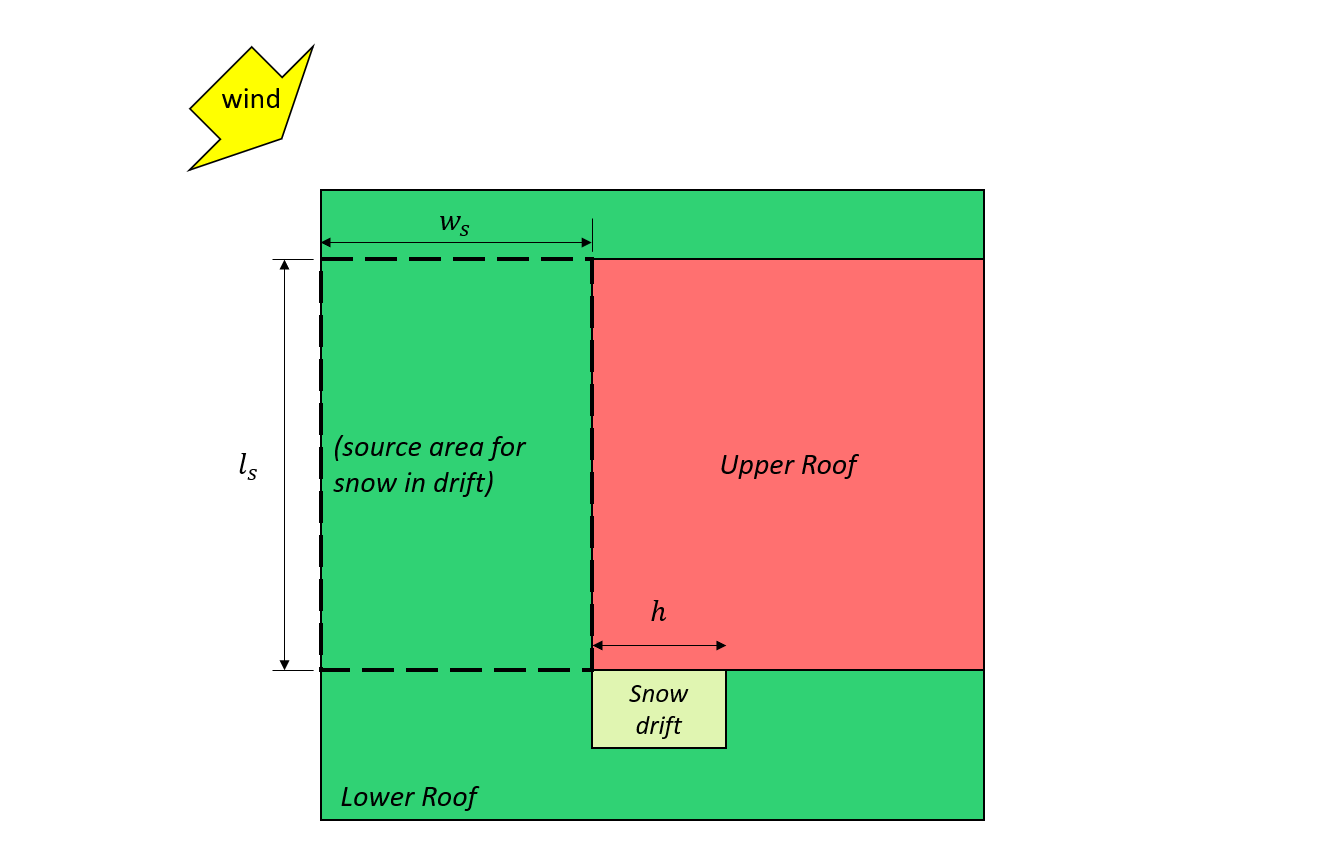
Figure 7: Cas III – neige partielle formée par le vent provenant du toit inférieur basé sur Graphique 4.1.6.5-B.
Dans cet exemple, Les cas I et II seront considérés.
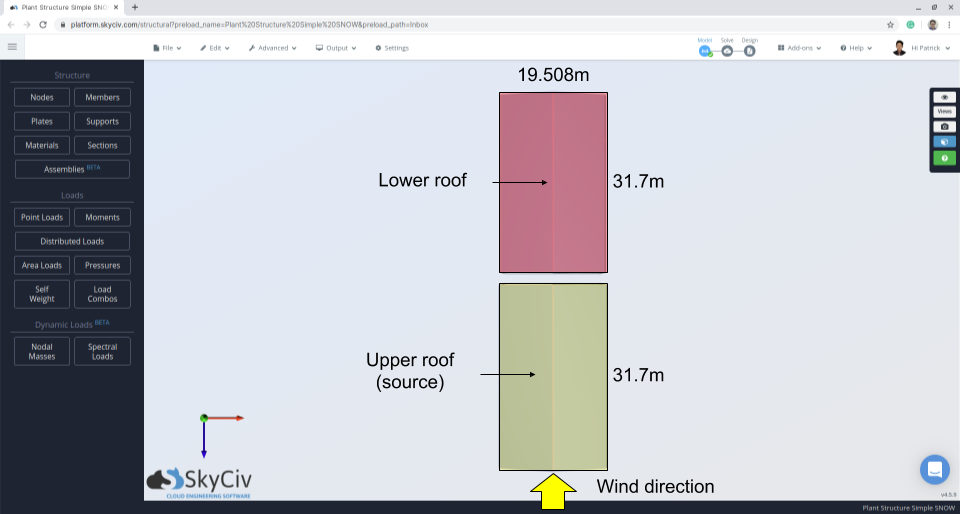
Figure 10: Plan de structure indiquant la direction du vent et la zone source.
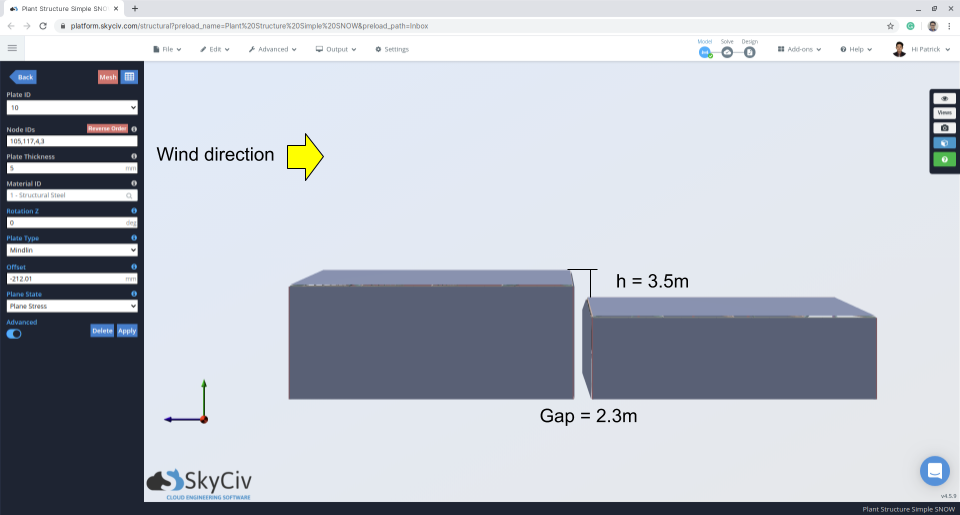
Figure 11: Vue d'élévation indiquant l'écart et la différence du toit supérieur et inférieur.
Pour le cas déséquilibré / dérivé parallèle à la crête, \({C}_{a}\) sont calculés pour les cas I et II sur la base 4.1.6.5 pour le toit à plusieurs niveaux. Pour le cas I, ces paramètres suivants doivent d'abord être calculés à l'aide des différentes équations mentionnées précédemment dans cet exemple:
\(β = 1.0\)
\({h}^{«} = (3.5) – \frac{(0.8)(1.0)(1.10)}{(2.673)} = 3.17 m )
\({h}_{p} = 0\)
\({{h}_{p}}^{«} =0\)
\({l}_{cs} = 2(19.507) -{(19.507)}^{2}/(31.7) = 27.01 m )
\(F = 0.35(1.0)\sqrt{\frac{(2.673)((27.01) – 5(0))}{(1.10)}} +(0.8) = 3.636\)
\({C}_{A0} = frac{(1.0)(2.673)(3.5)}{(0.8)(1.10)} = 10.631\) ou \({C}_{A0} = frac{3.66}{0.8} = 4.544\)
\({C}_{A0} = 4.544\)
\({X}_{d} = 5 \frac{(0.8)(1.10)}{2.673}(4.544 – 1) = 5.835 m )
À partir de ces paramètres, le facteur d'accumulation, \({C}_{a}\), peut être calculé en remplaçant la valeur de \({C}_{A0}\) à chaque \(X) distance. Notez que nous devons calculer \({C}_{a}\) à \(x = a ) où \(une) est l'écart entre le toit puisque l'écart du toit est inférieur à 5 m comme spécifié dans 4.1.6.6.
à \(x = 0\): \({C}_{a} = 4,544 – (4.544 – 1)(0/5.835) = 4.544\)
à \(x = a ): \({C}_{a} = 4,544 – (4.544 – 1)(2.3/5.835) = 3.147\)
à \(x = {X}_{d}\): \({C}_{a} =1.0\)
à \(x = 10{h}^{«}\): \({C}_{a} =1.0\)
w w w, \({C}_{s} = 1.0\). De plus, lors de la recherche de la charge de neige spécifiée sur le toit supérieur, le facteur d'accumulation, \({C}_{a}\), et facteur de pente, \({C}_{s}\), sont tous deux égaux à 1.0. Donc, l'ampleur des charges de neige spécifiées à chaque emplacement sont:
à \(x = 0\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(4.544) +0.1) = 3.279 kPa)
à \(x = a ): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(3.147) +0.1) = 2.295 kPa = {p}_{1}\)
à \(x = {X}_{d}\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa ={p}_{2} = {p}_{3}\)
au niveau supérieur du toit: \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa)
Vent agissant parallèlement à la crête – Cas II – Vent du toit inférieur au toit supérieur
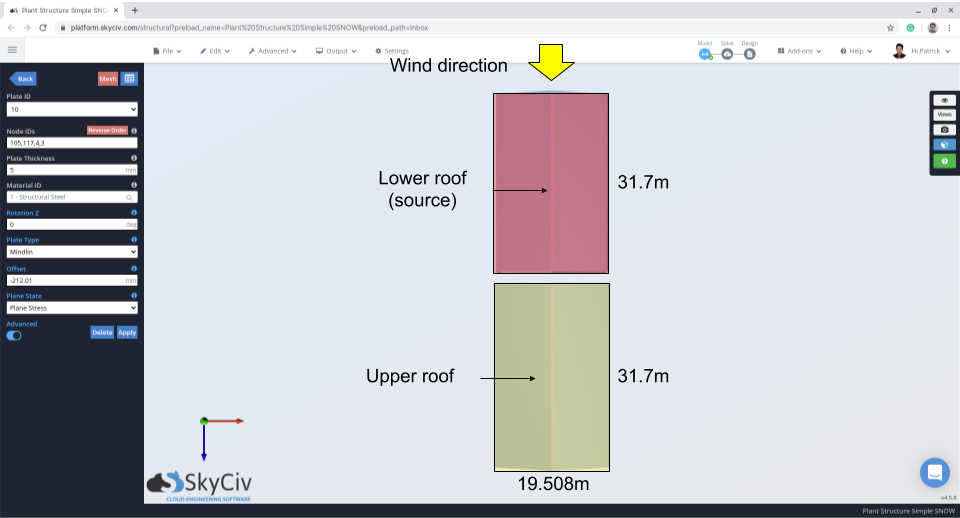
Figure 12: Plan de structure indiquant la direction du vent et la zone source – vent du bas du toit vers le haut.
Pour le cas II, le calcul est similaire au cas I mais a un \(β = 0.67\):
\(β = 0.67\)
\({h}^{«} = (3.5) – \frac{(0.8)(1.0)(1.10)}{(2.673)} = 3.17 m )
\({h}_{p} = 0\)
\({{h}_{p}}^{«} =0\)
\({l}_{cs} = 2(19.507) -{(19.507)}^{2}/(31.7) = 27.01 m )
\(F = 0.35(0.67)\sqrt{\frac{(2.673)((27.01) – 5(0))}{(1.10)}} +(0.8) = 2.70\)
\({C}_{A0} = frac{(1.0)(2.673)(3.5)}{(0.8)(1.10)} = 10.631\) ou \({C}_{A0} = frac{2.70}{0.8} = 3.375\)
\({C}_{A0} = 3.375\)
\({X}_{d} = 5 \frac{(0.8)(1.10)}{2.673}(3.375 – 1) = 3.909 m )
à \(x = 0\): \({C}_{a} = 3,375 – (3.375 – 1)(0/3.909) = 3.375\)
à \(x = a ): \({C}_{a} = 3,375 – (3.375 – 1)(2.3/3.909) = 1.978\)
à \(x = {X}_{d}\): \({C}_{a} =1.0\)
à \(x = 10{h}^{«}\): \({C}_{a} =1.0\)
à \(x = 0\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(3.375) +0.1) = 2.456 kPa)
à \(x = a ): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.978) +0.1) = 1.473 kPa = {p}_{1}\)
à \(x = {X}_{d}\): \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa = {p}_{2} = {p}_{3}\)
au niveau supérieur du toit: \(S = 0,8((1.10)(0.8)(1.0)(1.0)(1.0) +0.1) = 0.784 kPa)
Pour illustration, le correspondant \({p}_{1}\), \({p}_{2}\), et \({p}_{3}\) sont montrés dans les figures 13 et 14 ci-dessous pour les cas I et II, respectivement.
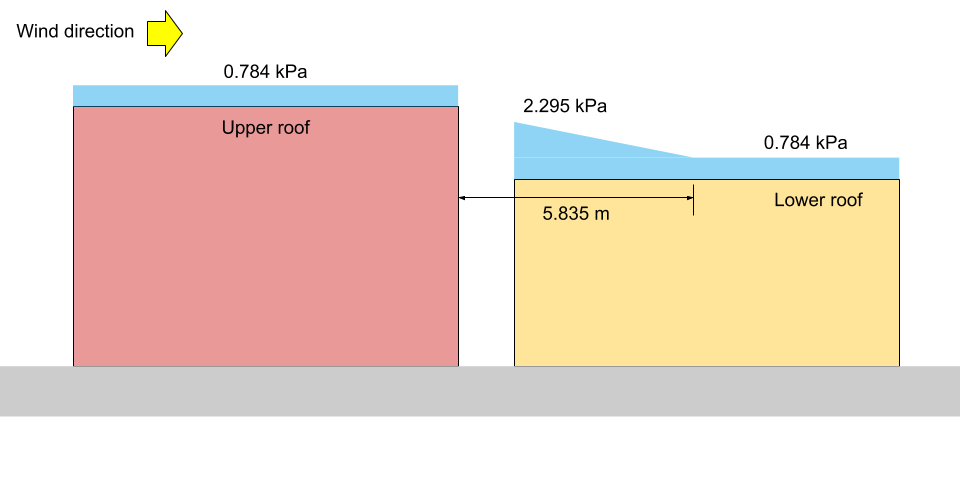
Figure 13: Illustration de la charge de neige pour le cas I (Pas à l'échelle).
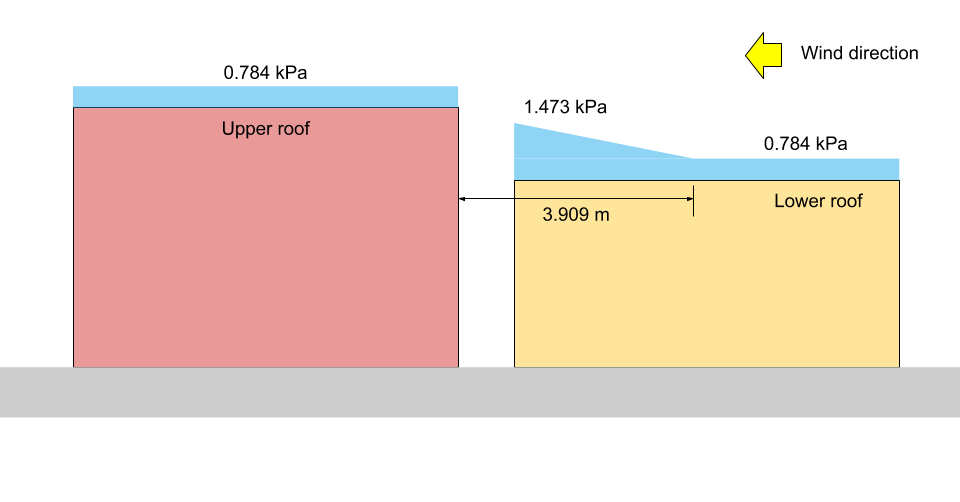
Figure 14: Illustration de la charge de neige pour le cas II (Pas à l'échelle).
Effectuez ces calculs automatiquement en quelques minutes
C'était un long calcul, que pouvez-vous faire en tant qu'ingénieur pour accélérer ce processus pour vos futurs projets? Récemment, SkyCiv a publié et automatisé le générateur de charge de neige dans le cadre du générateur de charge SkyCiv, qui peut également générer des charges de vent. Pour trouver les charges de neige de l'exemple illustré, il suffit de quelques clics en utilisant l'outil:
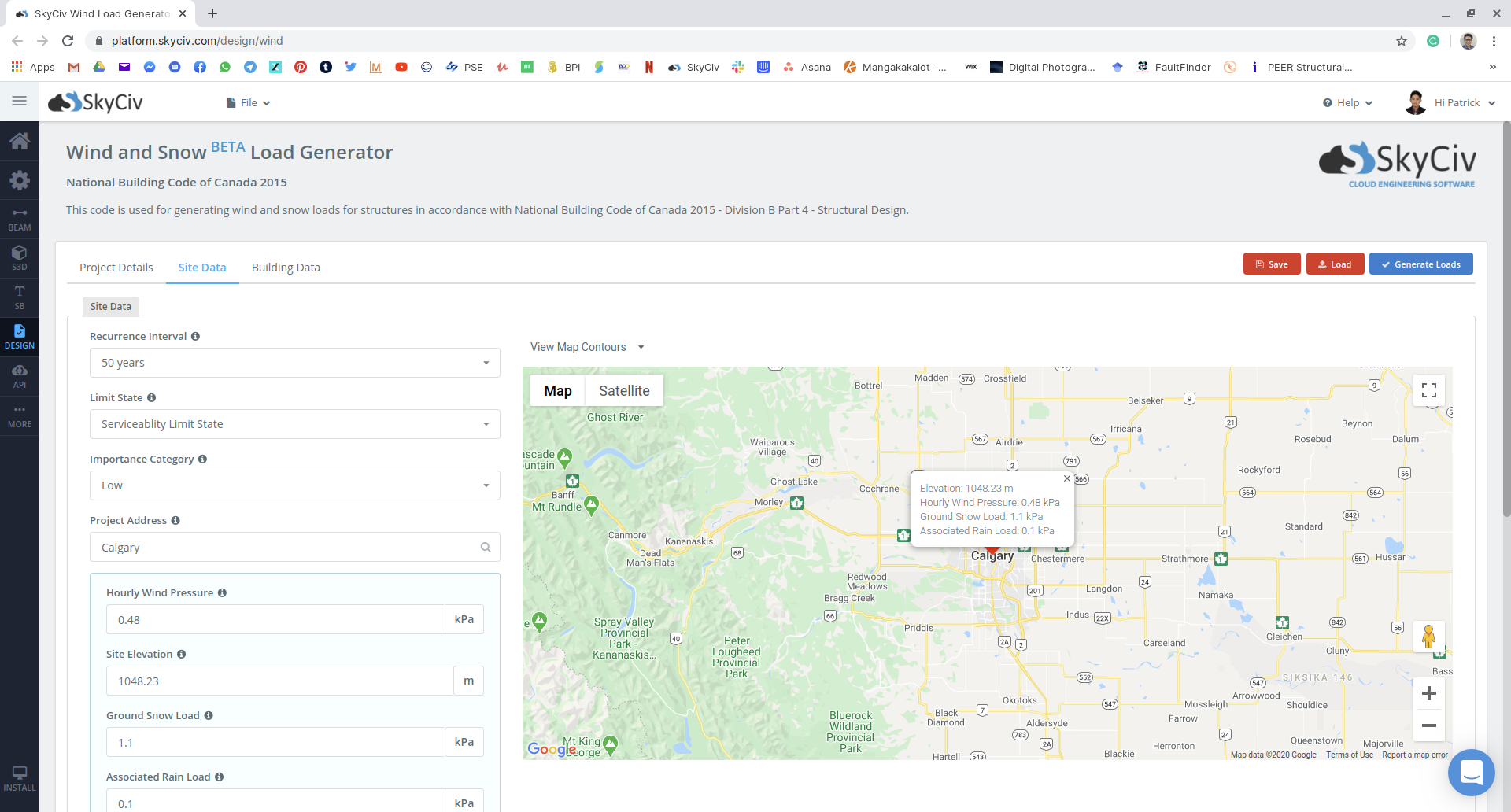
Figure 15: Entrée de données de site sur le module SkyCiv Load Generator en utilisant notre exemple.
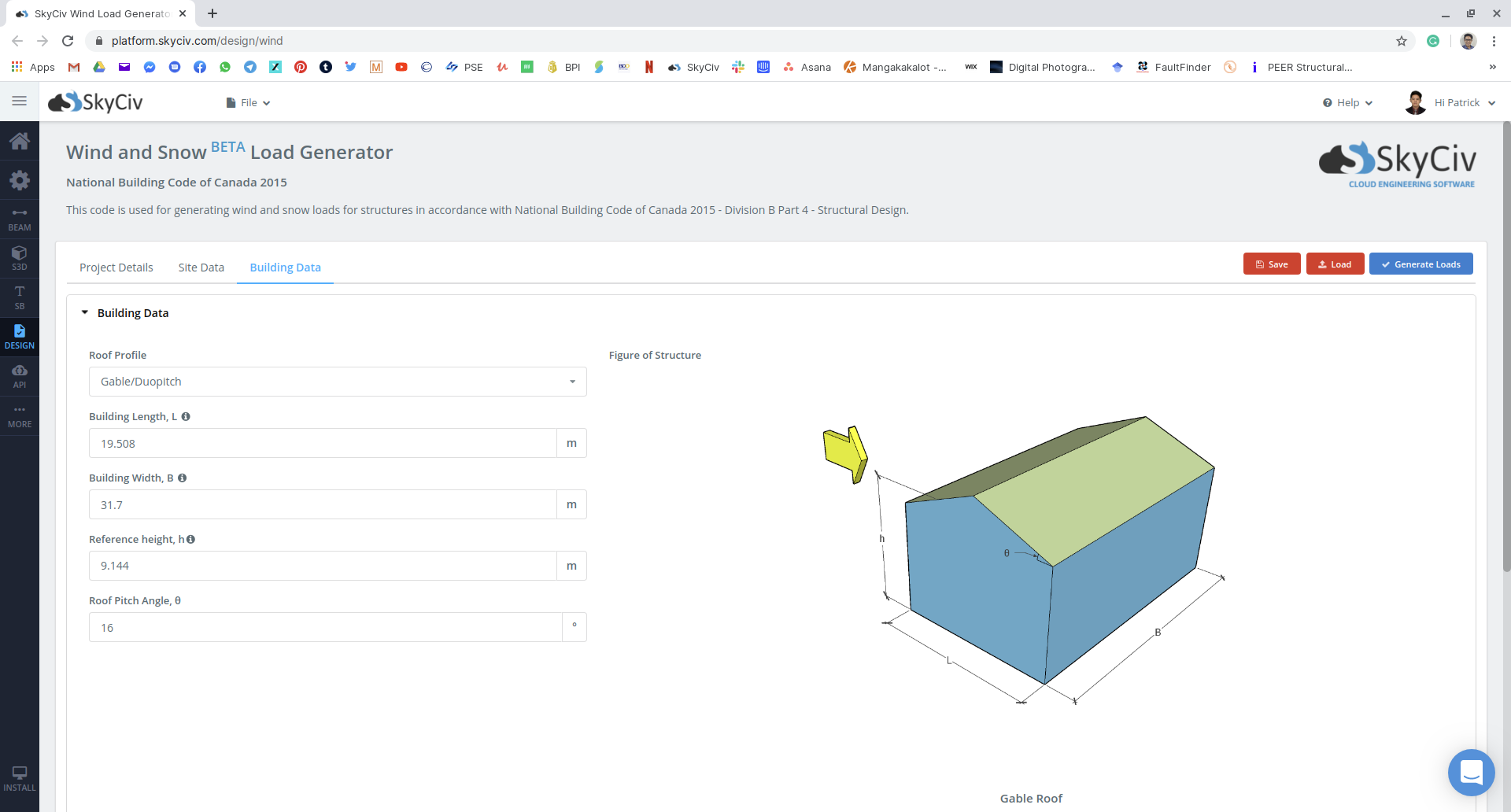
Figure 16: Entrée des paramètres de bâtiment et de neige sur le module SkyCiv Load Generator à l'aide de notre exemple.
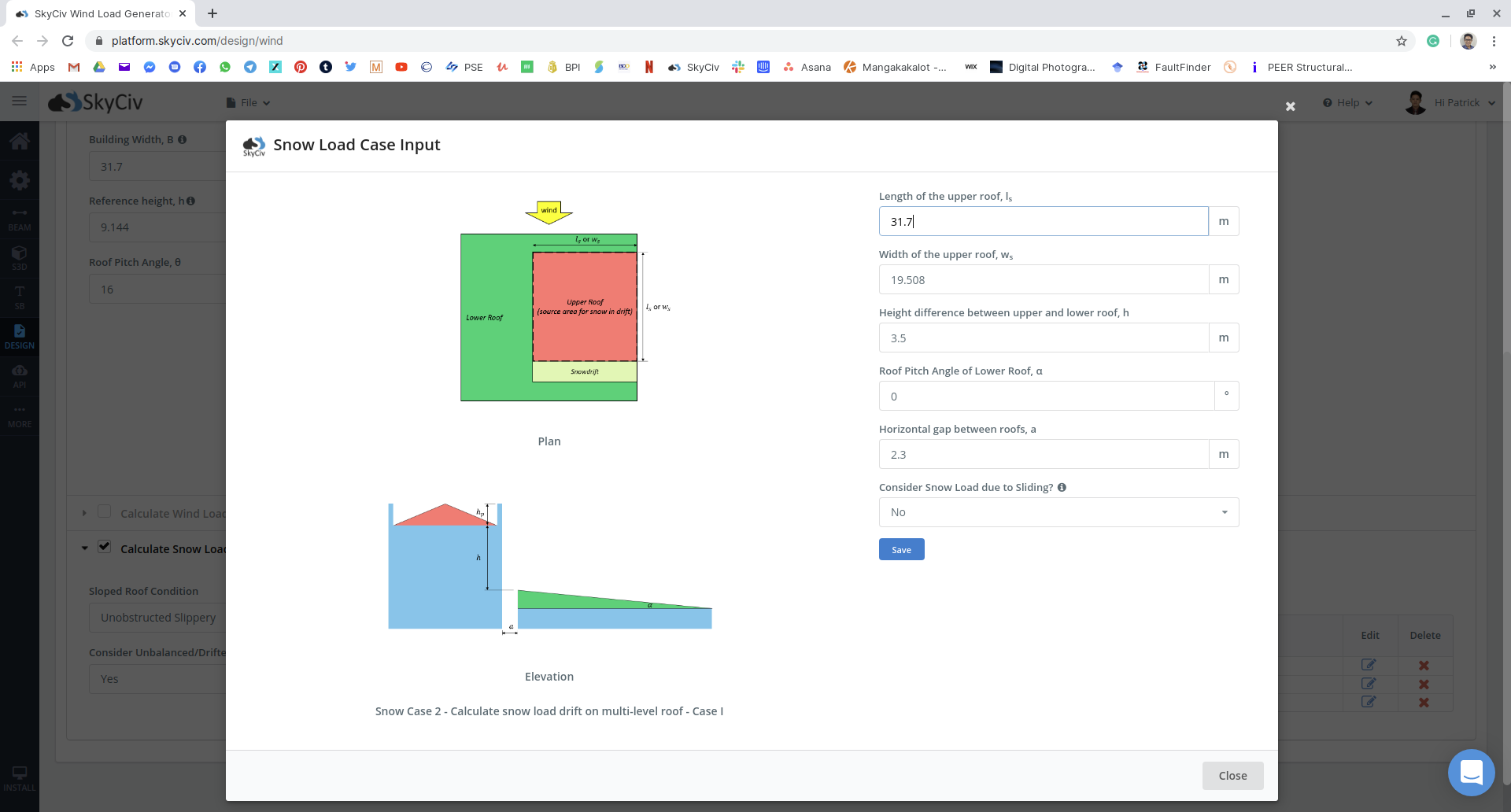
Figure 17: Entrée de charge de neige pour plusieurs cas asymétriques pour l'exemple.
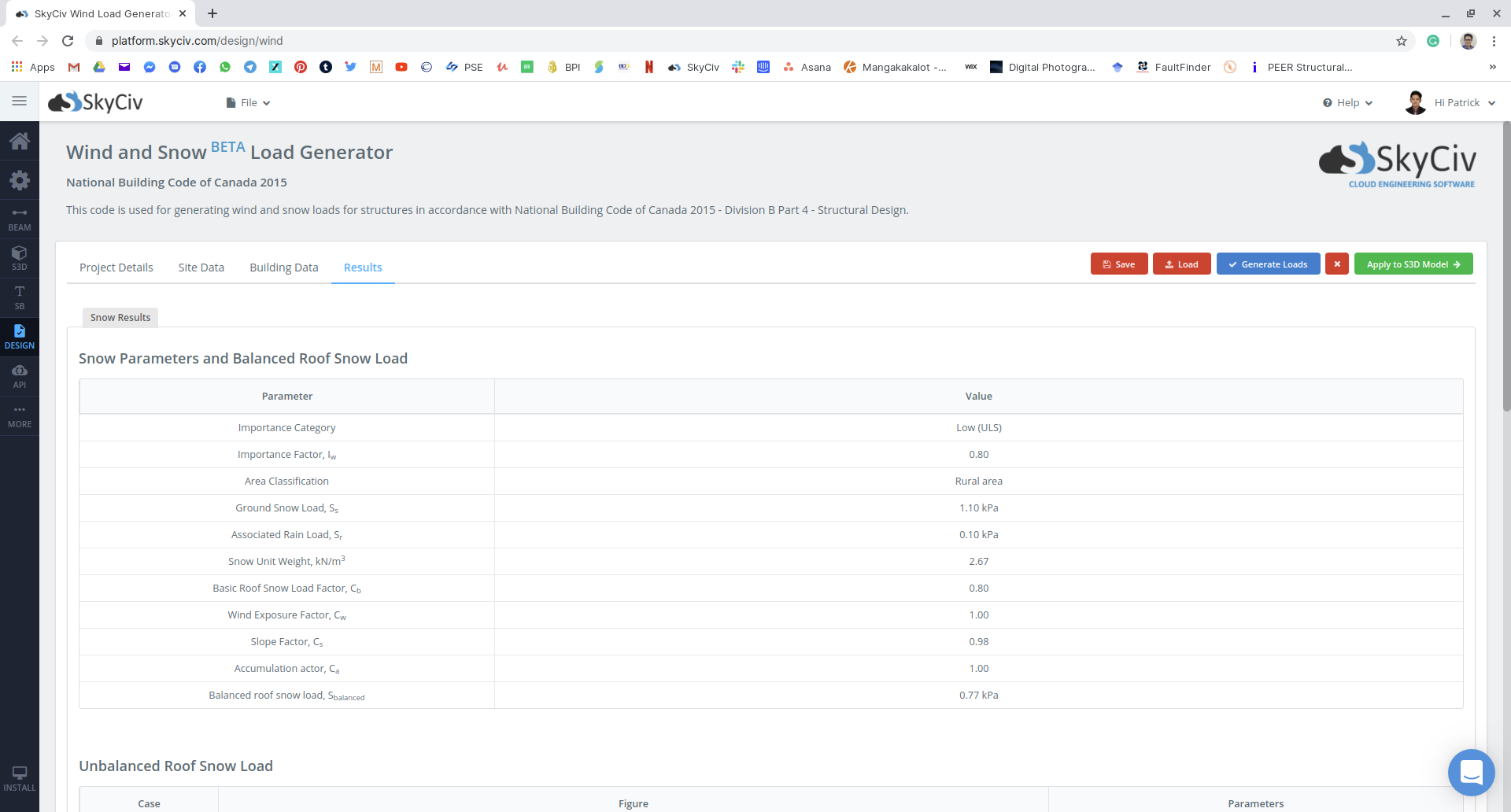
Figure 18: Résumé des paramètres de charge de neige utilisés et de la charge de neige équilibrée à appliquer à la structure.
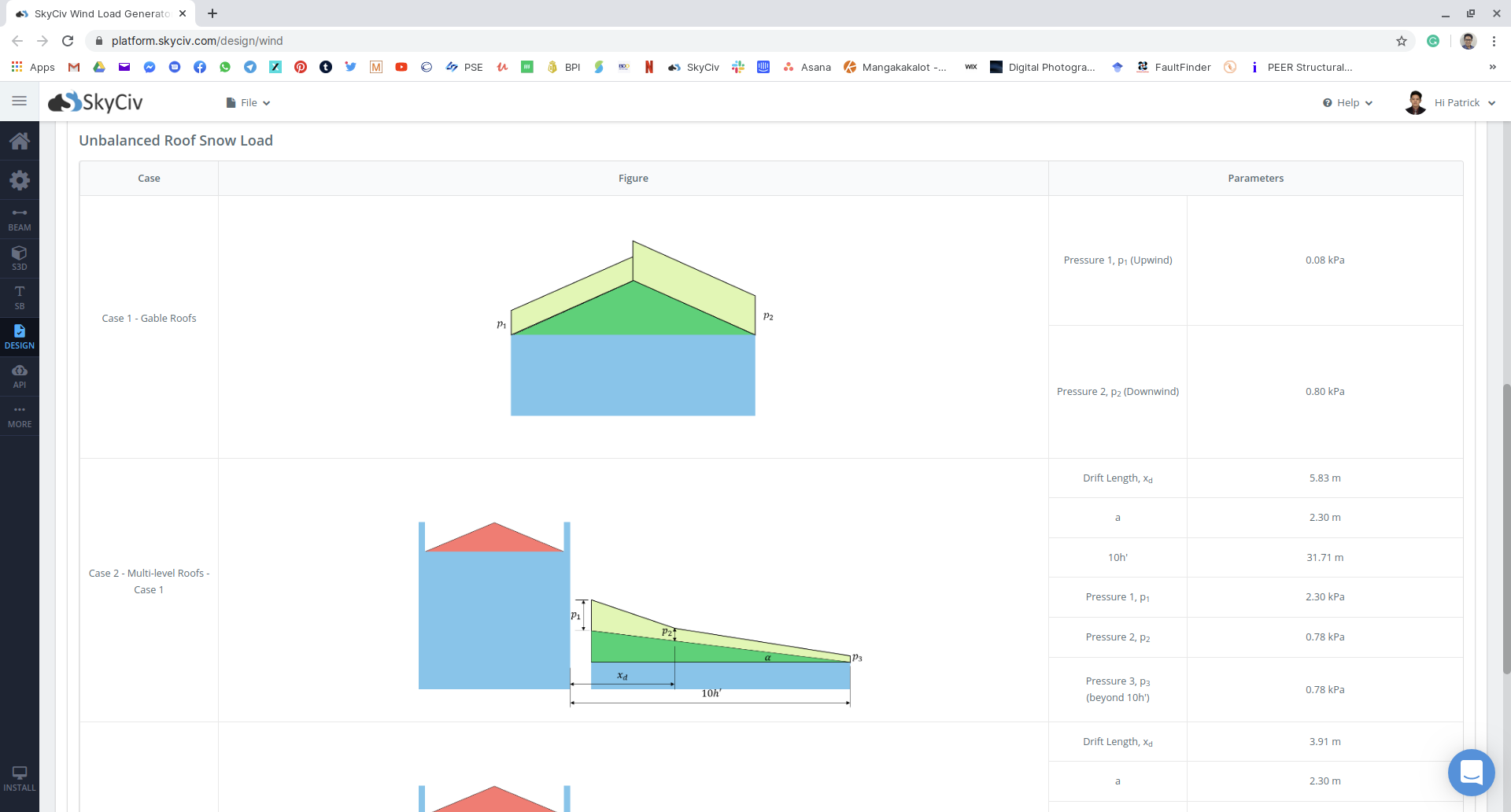
Figure 19: Résumé des résultats de charges de neige déséquilibrées.
Les calculs de charge de neige dans le module SkyCiv Load Generator sont pris en charge par des codes de référence tels que ASCE 7-10, 7-16, EN 1991-1-3, CNBC 2015, et AS / NZS 1170.3, et est disponible sur le Autonome (Générateur de charge uniquement) et Professionnel comptes. Familier avec la programmation et les API? Cette fonctionnalité peut être automatisée avec l'utilisation du API SkyCiv.
Ingénieur en structure, Développement de produits
MS Génie Civil
Références:
- Conseil national de recherches du Canada. (2015). Code national du bâtiment du Canada, 2015. Conseil national de recherches du Canada.
Remarque:
- Référence du code NBCC pour le “Facteur de charge de neige de base du toit” — chercher 4.1.6.2 Phrase (2)
- Référence du code NBCC pour le “Facteur d'exposition au vent” — chercher 4.1.6.2 Phrases (3) et (4)
- Référence du code NBCC pour le “Facteur de pente” — chercher 4.1.6.2 Phrases (5), (6), et (7)
- Référence du code NBCC pour le “Facteur d'accumulation” — chercher 4.1.6.2 Phrase (8), 4.1.6.5 pour toitures à plusieurs niveaux, 4.1.6.6 pour toitures avec fente, et 4.1.6.9 pour toits à pignon



