Description générale
SkyCiv dispose d'un module robuste et avancé pour la conception de dalles en béton armé. Pour accéder à cette fonctionnalité, vous devez d'abord avoir construit un modèle sur SkyCiv S3D puis appeler le module de calcul automatique avec différents codes de construction tels que ACI-318, Normes européennes et australiennes, etc. L'objectif principal du module pour la conception de plaques est de fournir la quantité de barres d'armature en acier le long de la plaque.
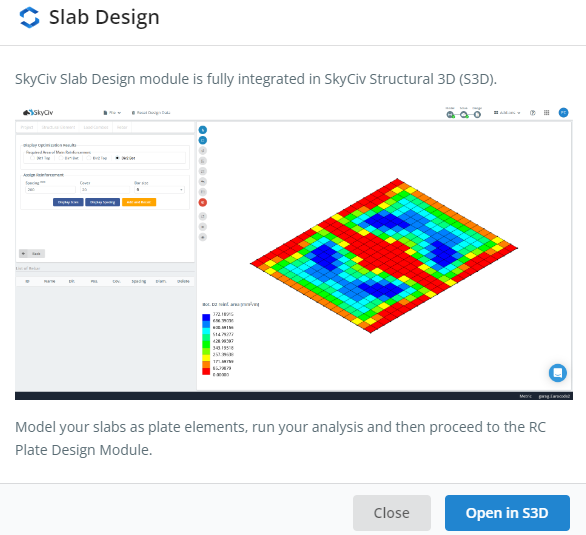
Figure 1. Module de conception de dalle SkyCiv
Si vous êtes nouveau chez SkyCiv, Inscrivez-vous et testez le logiciel vous-même!
La documentation SkyCiv fournit un excellent contenu, incluant des exemples et des cas d'analyse, à la fois pour savoir si vous êtes nouveau dans les modules et pour comparer les résultats du module de conception de plaques avec des calculs manuels. N'hésitez pas à consulter nos exemples de conception selon ACI-318, Eurocode, et AS3600.
Nous vous suggérons de lire cet article avant d'analyser en profondeur les systèmes de dalles complexes. Ici, vous apprendrez comment les moments fléchissants diffèrent selon les dimensions du plan de dalle. Il y a deux cas d'études, dalles unidirectionnelles et bidirectionnelles. Donc, commençons à lire!
Comportement de dalle unidirectionnel ou bidirectionnel
Considérons l'exemple de dalle dans l'image suivante, où il y a un appui sur chaque bord de dalle, et nous établissons que cela se comportera comme une plaque à double sens, C'est, ayant un moment de flexion dans les deux directions principales du plan.
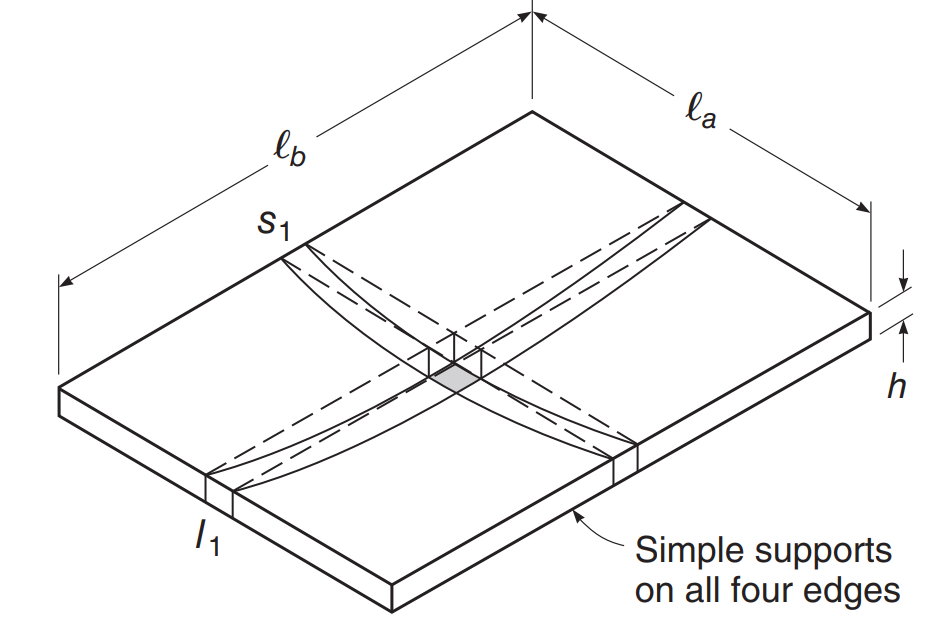
Figure 2. Exemple simple de dalle bidirectionnelle en flexion. (David Darwin, Charles W. Dolan, Arthur H.. Nilson, “Conception de structures en béton,” Quinzième édition, Éducation McGraw-Hill)
On peut définir le déplacement vertical comme (\(la < kg \)):
\(\Delta_a = frac{{5}{Washington}{l_a^4}}{384{E}{I}}\)
\(\Delta_b = frac{{5}{w_b}{l_b^4}}{384{E}{I}}\)
Étant donné que la dalle est un système continu, les deux déviations verticales auront la même valeur. On peut comparer les équations pour exprimer une relation entre la charge portée par chaque direction en fonction des dimensions du plan.
\(\Delta_a = \Delta_b \to \frac{{5}{Washington}{l_a^4}}{384{E}{I}} = frac{{5}{w_b}{l_b^4}}{384{E}{I}}\)
\(\frac{Washington}{w_b} = {(\frac{kg}{la}})^ 4 \)
Toutes les références en béton armé pour la conception de dalles se divisent en unidirectionnelles et bidirectionnelles si le quotient de \(\frac{kg}{la}\) est supérieur ou inférieur à une valeur de 2, respectivement.
En utilisant les équations ci-dessus, quand \(\frac{kg}{la}=2\), la charge portée par la direction courte est égale à \(w_a = {16}{w_b}\) et quand la valeur est \(\frac{kg}{la}=1\), la charge est répartie équitablement dans les deux sens \(w_a ={w_b}\).
Moments de dalles à sens unique
Donc, on voit que lorsque le quotient des dimensions est supérieur à 2, pratiquement, toutes les charges et moments de flexion seront concentrés uniquement dans la direction courte. Ce cas est le comportement unidirectionnel de la dalle, et le moment de flexion maximum peut être obtenu comme une poutre simplement appuyée avec une largeur unitaire.
\(M_{max,1,D}= frac{{Washington}{1 m}{l_a^2}}{8}\)
Moments de dalles à double sens
La solution du cas de la dalle bidirectionnelle est un problème complexe et difficile en mécanique des structures. Vous pouvez voir dans la figure ci-dessous que l'analyse générale consiste en une plaque avec des forces et des moments entiers dans chaque direction.
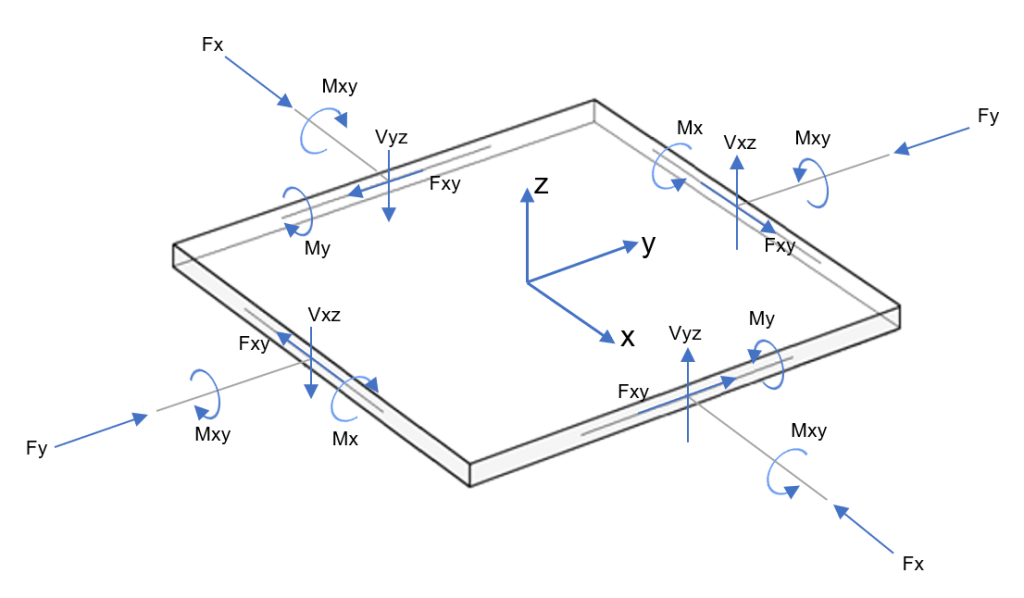
Figure 3. Actions sur l'élément de plaque (moments de flexion et de torsion; forces normales et de cisaillement)
Cette difficulté vient du fait que le problème à résoudre est une équation aux dérivées partielles du quatrième ordre qui implique la flexion dans deux directions. La forme de cette équation est:
\(\frac{\partiel ^ 4{w}}{{\partiel}{x^4}} + {2}\frac{{\partiel ^ 4}{w}}{{{\partiel}{x^2}}{{\partiel}{y ^ 2}}}+\frac{\partiel ^ 4{w}}{{\partiel}{x^4}}-\frac{f_z}{D} = 0\)
Où la rigidité de la plaque (en utilisant les propriétés mécaniques et géométriques élastiques) est \(D=\frac{{E}{t ^ 3}}{{12}{(1-\non ^ 2)}}\).
La solution analytique de cette équation n'est disponible que pour des conditions d'appui simples. La seule façon d'obtenir une solution possible pour des cas réels et pratiques consiste à utiliser des méthodes numériques telles que la méthode des éléments finis..
SkyCiv utilise cette approche pour résoudre l'analyse des plaques. Sur les liens suivants, vous aurez accès à des tutoriels pour en savoir plus sur les caractéristiques de la plateforme SkyCiv: Conception de plaque en S3D et Comment modéliser des plaques? .
Si vous êtes nouveau chez SkyCiv, Inscrivez-vous et testez le logiciel vous-même!


