Cet article traite de deux exemples de conception de dalles en béton armé, y compris le pliage unidirectionnel et bidirectionnel. L'objectif principal est de comparer les résultats obtenus entre les calculs manuels et le module de conception de plaques SkyCiv. Nous utiliserons l'Eurocode 2 pour les structures en béton armé.
Les codes de construction ont des approches similaires lors de la définition des cas typiques pour les dalles. Si vous voulez en savoir un peu plus sur ce sujet, nous vous suggérons de lire les articles suivants concernant la conception des dalles Exemple de conception de dalle ACI et comparaison avec SkyCiv et Normes australiennes Exemple de conception de dalle AS3600 et comparaison avec SkyCiv
Exemple de conception de dalle unidirectionnelle
Le premier cas à analyser est un petit immeuble d'un étage (Figure 1, Figure 2) qui a un comportement de dalle décrit comme dans une direction.
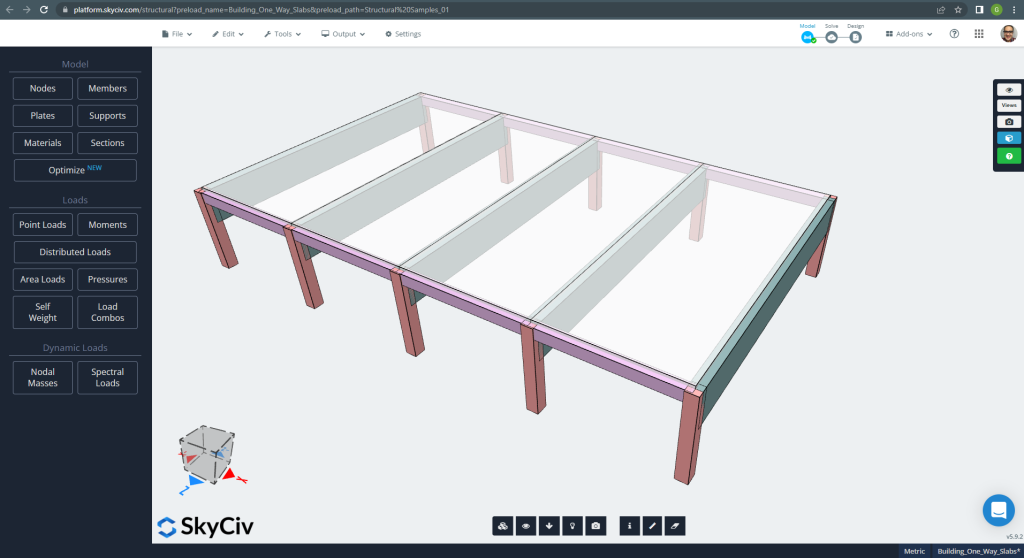
Figure 1. Exemple de dalles unidirectionnelles dans un petit bâtiment. (Structural 3D, Ingénierie Cloud SkyCiv).
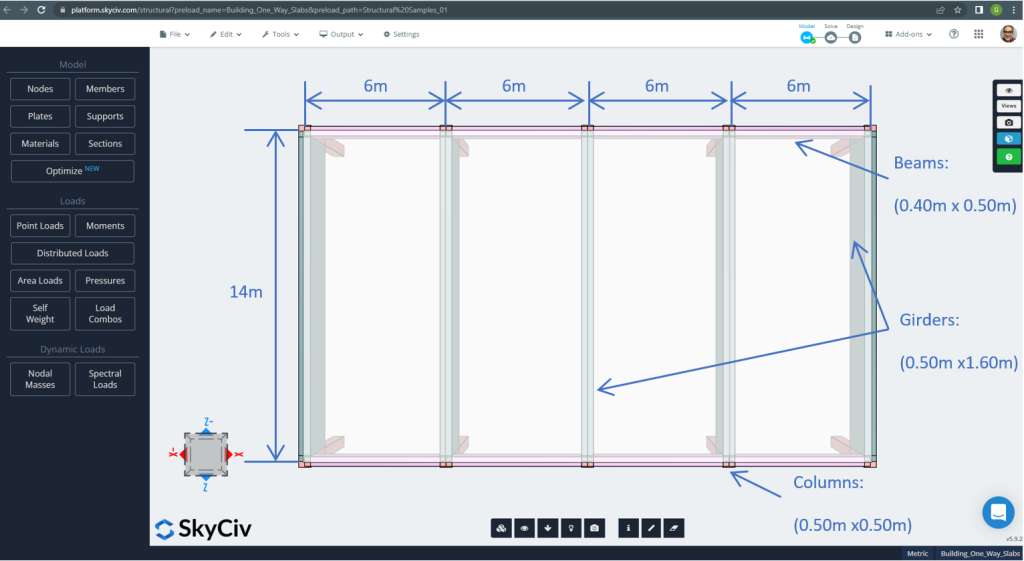
Figure 2. Exemple de dalles unidirectionnelles dans un petit bâtiment (dimensions du plan). (Structural 3D, Ingénierie Cloud SkyCiv).
Pour l'exemple de la dalle, en résumé, le matériel, propriétés des éléments, et les charges à considérer :
- Classement des types de dalles: Une – comportement de manière \(\frac{L_2}{L_1} > 2 ; \frac{14m}{6m}=2,33 > 2.00 \) D'accord!
- Occupation du bâtiment: Usage résidentiel
- Épaisseur de la dalle \(t_{dalle}=0.25m\)
- Densité du béton armé \(\rho_w = 25 \frac{kN}{m^3}\)
- Résistance caractéristique à la compression du béton à 28 journées (C25\30) \(fck = 25 MPa \)
- Poids propre de la dalle \(Dead = \rho_w \times t_{dalle} = 25 \frac{kN}{m^3} \fois 0.25m = 6.25 \frac {kN}{m^2}\)
- Charge morte superposée \(ET = 3.0 \frac {kN}{m^2}\)
- Charge vive \(L = 2.0 \frac {kN}{m^2}\)
Calculs manuels selon EN-2
Dans cette section, nous calculerons l'armature en acier renforcée requise en utilisant la référence de la norme Eurocode. Nous obtenons d'abord le moment de flexion total pondéré à effectuer par la bande de largeur unitaire de la dalle.
- Poids mort, \(g = (3.0 + 6.25) \frac{kN}{m^2} \fois 1 m = 9.25 \frac{kN}{m}\)
- Charge vive, \(q = (2.0) \frac{kN}{m^2} \fois 1 m = 2.0 \frac{kN}{m}\)
- Charge ultime, \(Fd = 1.35\times g + 1.5\fois q = (1.35\fois 9.25 + 1.5\fois 2.0)\frac{kN}{m} =15.5 \frac{kN}{m} \)
Avant d'obtenir la zone d'armature en acier, nous devons vérifier les rapports de profondeur efficaces. Deux cas principaux:
| Système structurel | Rapport de base entre la portée et la profondeur effective | ||
|---|---|---|---|
| Facteur pour le système structurel K | Béton fortement sollicité %(\(\rho = 1.5 )\) | Béton légèrement sollicité %(\(\rho = 0.5 )\) | |
| 1. Portée d'extrémité d'une poutre continue ou d'une dalle continue unidirectionnelle ou d'une dalle bidirectionnelle continue sur un côté long | 1.3 | 18 | 26 |
| 2. Portée intérieure d'une poutre continue ou d'une dalle portante unidirectionnelle ou bidirectionnelle | 1.5 | 20 | 30 |
Le cas le plus critique est pour le numéro un, donc, nous sélectionnons un rapport de 26.
- \(t_{min}= frac{L}{JE SAIS}+cover+0.5\dot bar_{diamètre}= frac{6m}{26}+0.025m+0.5\times 12mm=0.26m \) ~ \(0.25m ). L'épaisseur globale est encore suffisante, D'accord!
Maintenant, il est temps d'utiliser le tableau pour les dalles continues unidirectionnelles:
| Condition de fin de prise en charge | Au premier soutien intérieur | Au milieu des travées intérieures | Aux supports intérieurs | ||||
|---|---|---|---|---|---|---|---|
| Épinglé | Continu | ||||||
| Support extérieur | Près du milieu de la portée d'extrémité | Fin de l'assistance | Portée de fin | ||||
| Moment | 0 | 0.086Floride | – | 0.075Floride | – | 0.063Floride | – |
| 0.04Floride | 0.086Floride | 0.063Floride | |||||
| Tondre | 0.4F | – | – | – | |||
| 0.46F | 0.6F | 0.5F | |||||
Où:
- L est la portée effective
- F est la charge ultime totale dans la travée (1.35Gk + 1.5Qk; Gk est la charge permanente et Qk la surcharge, respectivement)
Il ne sera expliqué qu'un seul cas (support de fin continu) et le reste apparaîtra dans le tableau suivant.
- \(F=Fd\times L = 15.5 \frac{kN}{m} \fois 6m = 93.0 kN \)
- \(M=0.04FL=0.04 \times 93.0 kN \times 6m= -22.32{kN}{m}\)
- \(d = 230 mm \)
- \(K=\frac{M}{{b}{j^2}{F_{afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués}}}= frac{22.32\fois 10^6 {N}{mm}}{{1000mm}\fois{(230 mm)^ 2}\fois {25 \frac{N}{mm^2}}}=0.016877\)
- \(l_a = 0.95 \)
- \(z=l_a \times d = 0.95\times 230mm = 218.50 mm)
- \(A_s = frac{M}{{0.87}{F_{beurk}}{z}}= frac{22.32\fois 10^6 {N}{mm}}{0.87\fois 500 {N}{mm^2} \fois {218.50mm} = 234.83 mm^2 }\)
- \(UNE_{s,min}=0,0013{b}{d}=0.0013\times 1000mm \times 230 mm =299 mm^2\)
- \(UNE_{st}=max(Comme, UNE_{s,min}) = maximum(234.83, 299) mm^2 = 299 mm^2 \)
| Des moments | Extérieur négatif gauche | Extérieur positif | Extérieur négatif droit | Intérieur négatif gauche | Positif intérieur | Intérieur Négatif Droit |
|---|---|---|---|---|---|---|
| Valeur M, kN-m | 22.32 | 35.15 | 41.85 | 48.00 | 35.15 | 35.15 |
| K | 0.0168 | 0.0266 | 0.03164 | 0.0362 | 0.0266 | 0.0266 |
| z, mm | 218.50 | 218.50 | 218.50 | 218.50 | 218.50 | 218.50 |
| \(Comme, mm^2\) | 234.83 | 369.815 | 440.31 | 505.011 | 369.815 | 369.815 |
| \(UNE_{s,min},mm^2\) | 299.00 | 299.00 | 299.00 | 299.00 | 299.00 | 299.00 |
| \(UNE_{st} {mm^2}\) | 299.00 | 369.815 | 440.31 | 505.011 | 369.815 | 369.815 |
La prochaine étape consiste à calculer l'acier des barres d'armature à l'aide du module de conception de plaques dans SkyCiv. S'il te plaît, continuez à lire la section suivante!.
Si vous êtes nouveau chez SkyCiv, Inscrivez-vous et testez le logiciel vous-même!
Résultats du module de conception de plaques SkyCiv S3D
Cette section traite de l'obtention de la zone d'armature en acier mais uniquement à l'aide du logiciel, l' Module de conception de plaques. De façon concise, nous ne montrerons les résultats ou les informations importantes qu'à travers des images.
Avant d'analyser le modèle, il faut définir un maillage de plaque. Quelques références (2) recommander une taille pour l'élément coque de 1/6 de la courte portée ou 1/8 de la longue portée, le plus court d'entre eux. Suite à cette valeur, nous avons \(\frac{L2}{6}= frac{6m}{6} = 1m \) ou \(\frac{L1}{8}= frac{14m}{8}=1.75m \); nous prenons 1 m comme taille maximale recommandée et 0,50 m de maillage appliqué.
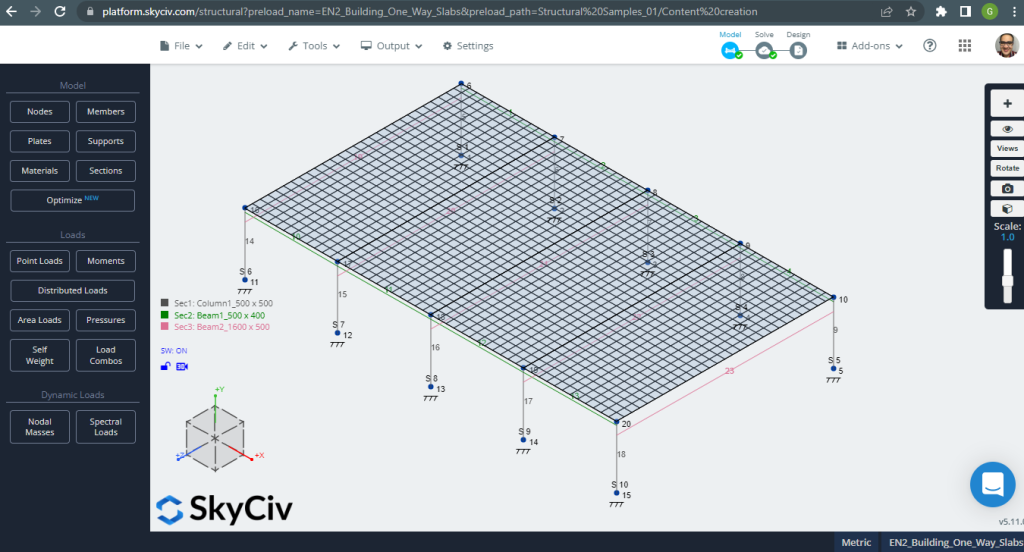
Figure 3. Plaque maillée. (Structural 3D, Ingénierie Cloud SkyCiv).
Une fois que nous avons amélioré notre modèle structurel analytique, nous exécutons une analyse élastique linéaire. Lors de la conception des dalles, nous devons vérifier si le déplacement vertical est inférieur au maximum autorisé par le code. Eurocode 2 établi un déplacement vertical de service maximum de \(\frac{L}{250}= frac{6000mm}{250}=24.0 mm\).
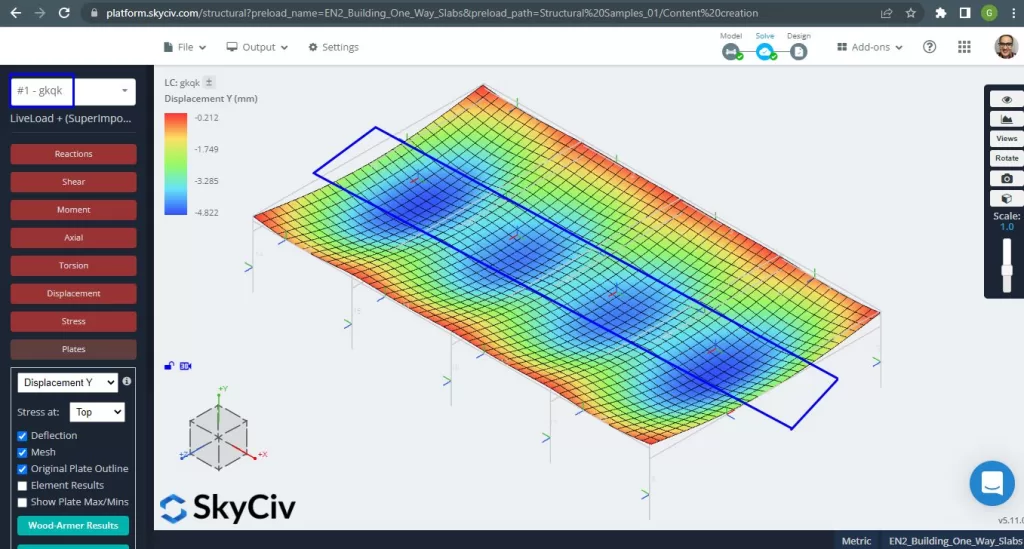
Figure 4. Déplacement vertical, valeurs maximales au centre des travées. (Structural 3D, Ingénierie Cloud SkyCiv).
Comparaison du déplacement vertical maximal avec la valeur référencée par le code, la rigidité de la dalle est suffisante. \(4.822 mm < 24.00mm).
Les moments maximaux dans les portées de la dalle sont situés pour le positif au centre et pour le négatif aux appuis extérieurs et intérieurs. Voyons ces valeurs de moments dans les images suivantes.
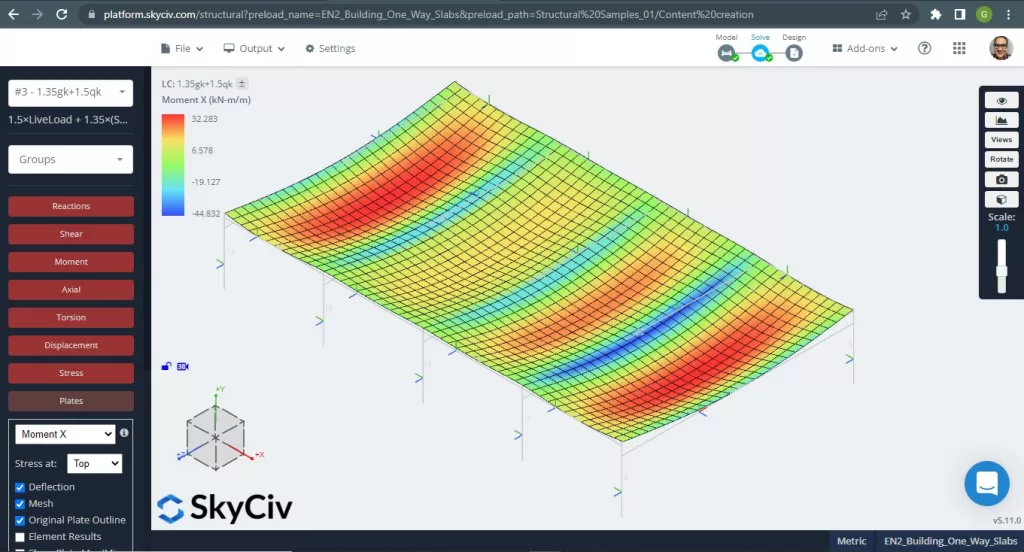
Figure 5. Moments de flexion dans la direction X. (Structural 3D, Ingénierie Cloud SkyCiv).
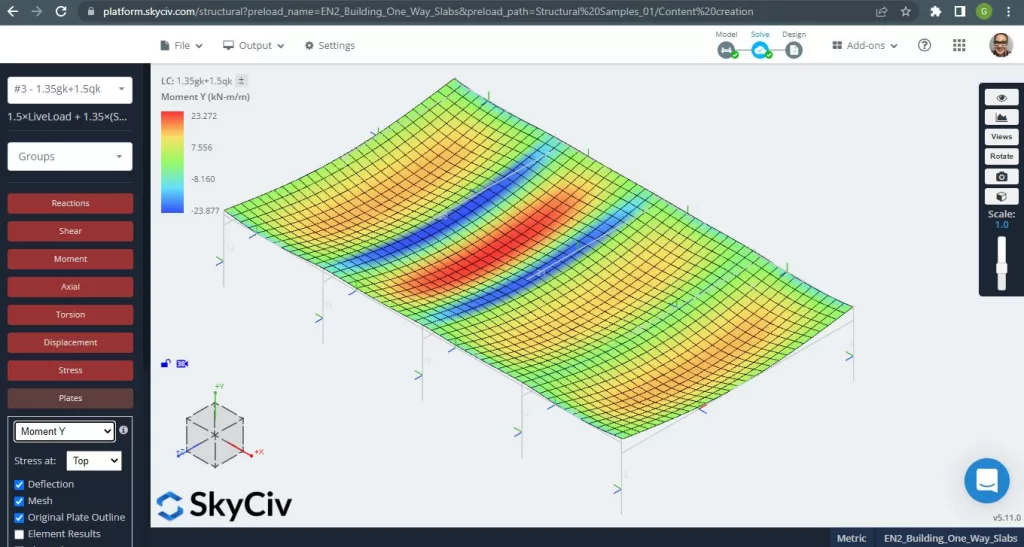
Figure 6. Moments de flexion dans la direction Y. (Structural 3D, Ingénierie Cloud SkyCiv).
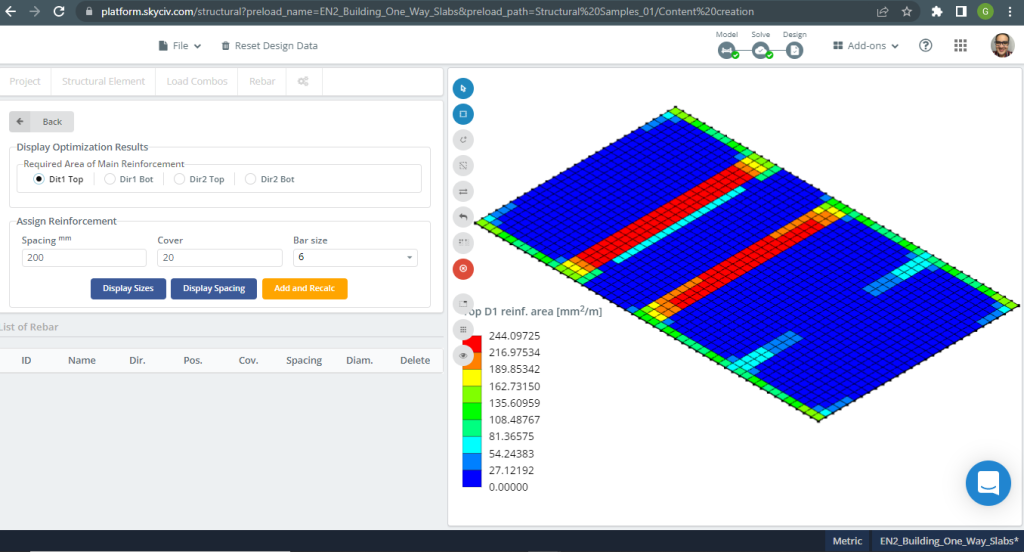
Figure 7. Renforcement en acier pour la direction X en haut. (Structural 3D, Ingénierie Cloud SkyCiv).
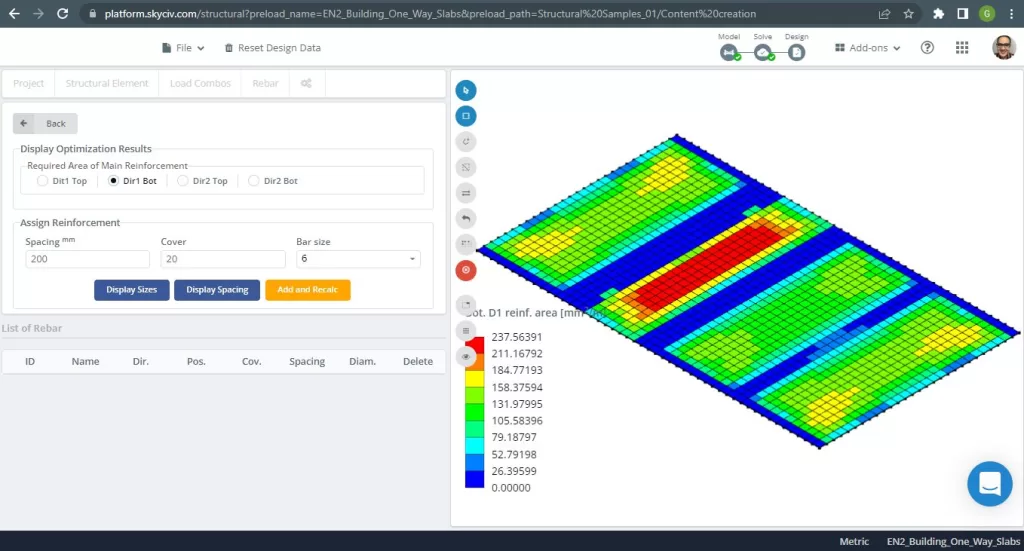
Figure 8. Renforcement en acier pour la direction X en bas. (Structural 3D, Ingénierie Cloud SkyCiv).
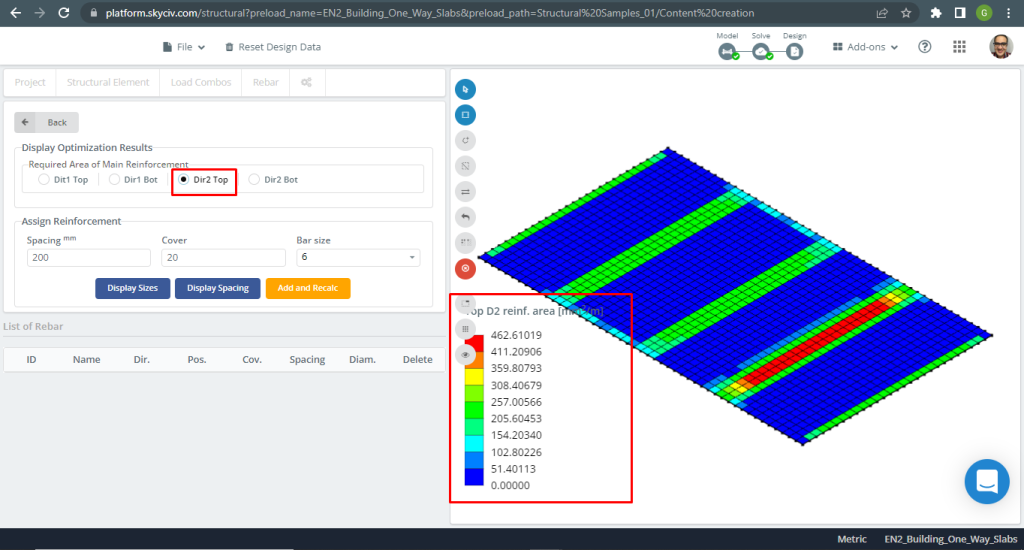
Figure 9. Renforcement en acier pour la direction Y en haut. (Structural 3D, Ingénierie Cloud SkyCiv).
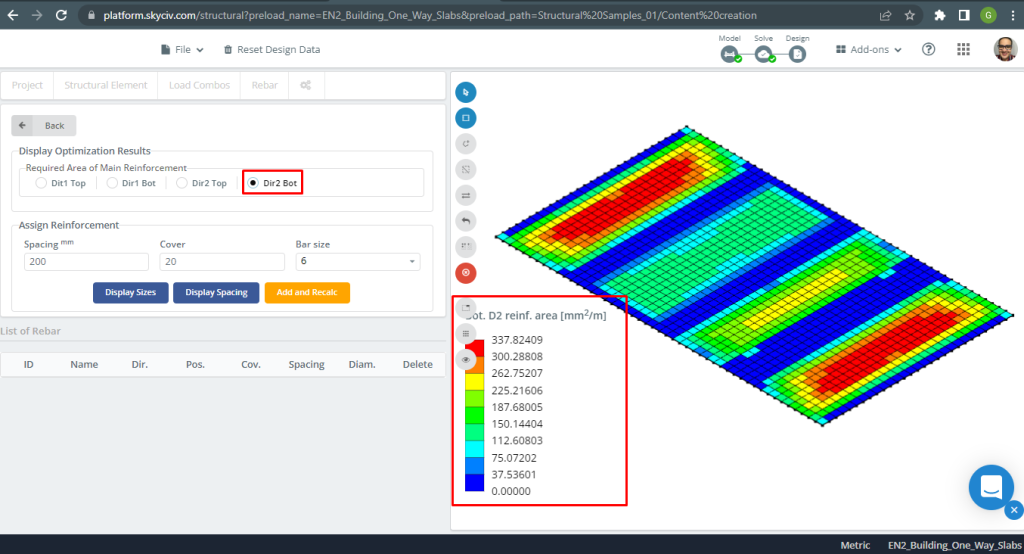
Figure 10. Renforcement en acier pour la direction Y en bas. (Structural 3D, Ingénierie Cloud SkyCiv).
Comparaison des résultats
La dernière étape de cet exemple de conception de dalle à sens unique consiste à comparer la zone d'armature en acier obtenue par analyse S3D (axes locaux “2”) et calculs manuels.
| Moments et zone d'acier | Extérieur négatif gauche | Extérieur positif | Extérieur négatif droit | Intérieur négatif gauche | Positif intérieur | Intérieur Négatif Droit |
|---|---|---|---|---|---|---|
| \(UNE_{st, Calculs manuels} {mm^2}\) | 299.00 | 369.82 | 440.31 | 505.011 | 369.82 | 369.82 |
| \(UNE_{st, S3D} {mm^2}\) | 308.41 | 337.82 | 462.61 | 462.61 | 262.75 | 308.41 |
| \(\Delta_{dif}\) (%) | 3.051 | 8.653 | 4.820 | 8.400 | 28.95 | 16.610 |
Nous pouvons voir que les résultats des valeurs sont très proches les uns des autres. Cela signifie que les calculs sont corrects!
Si vous êtes nouveau chez SkyCiv, Inscrivez-vous et testez le logiciel vous-même!
Exemple de conception de dalle bidirectionnelle
SkyCiv 3D Plate Design Module est un logiciel puissant qui peut analyser et concevoir tout type de bâtiment que vous pouvez imager. Pour le deuxième exemple de dalle de conception, nous avons décidé d'utiliser un système de dalles plates (figure 11).
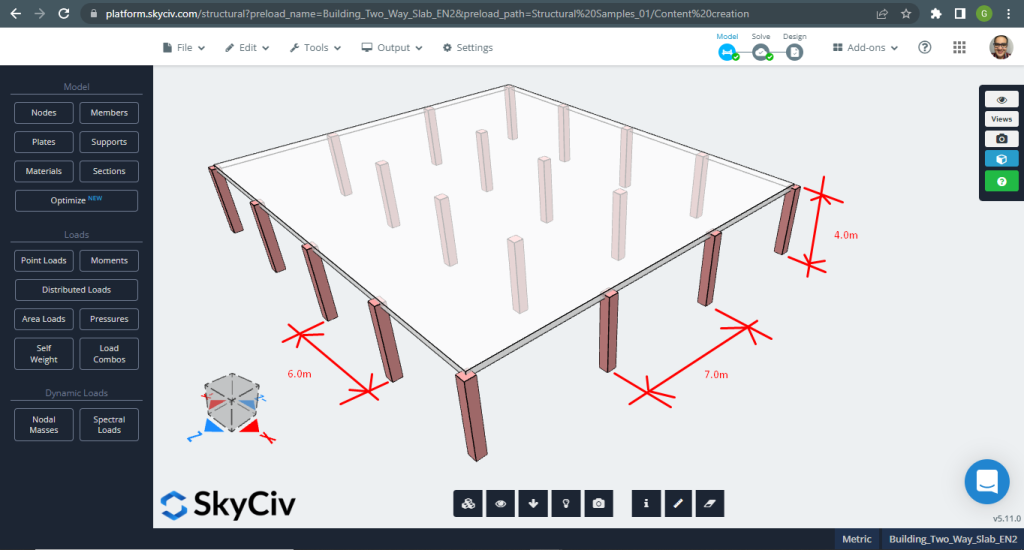
Figure 11. Exemple de dalles unidirectionnelles dans un petit bâtiment. (Structural 3D, Ingénierie Cloud SkyCiv).
Pour l'exemple de la dalle, en résumé, le matériel, propriétés des éléments, et les charges à considérer :
- Classement des types de dalles: Deux – comportement de manière \(\frac{L_2}{L_1} \le 2 ; \frac{7m}{6m}=1.17 \le 2.00 \) D'accord!
- Occupation du bâtiment: Usage résidentiel
- Épaisseur de la dalle \(t_{dalle}=0.30m\)
- Densité du béton armé \(\rho_w = 25 \frac{kN}{m^3}\)
- Résistance caractéristique à la compression du béton à 28 journées (C25\30) \(fck = 25 MPa \)
- Poids propre de la dalle \(Dead = \rho_w \times t_{dalle} = 25 \frac{kN}{m^3} \fois 0.30m = 7.5 \frac {kN}{m^2}\)
- Charge morte superposée \(ET = 3.0 \frac {kN}{m^2}\)
- Charge vive \(L = 2.0 \frac {kN}{m^2}\)
Calculs manuels selon EN-2
La première étape consiste à définir la charge ultime totale:
- Poids mort, \(g = (3.0 + 7.5) \frac{kN}{m^2} \fois 7 m = 73.50 \frac{kN}{m}\)
- Charge vive, \(q = (2.0) \frac{kN}{m^2} \fois 7 m = 14.00 \frac{kN}{m}\)
- Charge ultime, \(Fd = 1.35\times g + 1.5\fois q = (1.35\fois 73.50 + 1.5\fois 14.00)\frac{kN}{m} =120.225 \frac{kN}{m} \)
Pour le calcul manuel, la structure doit être divisée en une série de cadres équivalents. Nous pouvons utiliser les méthodes suivantes pour atteindre cet objectif:
- Répartition des moments (Méthode Hardy Cross) pour l'analyse de cadre.
- Méthode de rigidité pour l'analyse de l'ossature sur ordinateur. Essayez notre Calculateur de matrice de rigidité.
- Une méthode simplifiée utilisant les coefficients des moments pour une direction unidirectionnelle ajustée aux exigences suivantes (Nous avons choisi cette méthode en raison de la simplicité du modèle analysé):
- La stabilité latérale ne dépend pas des liaisons dalle-poteau (Nous n'analysons pas le bâtiment pour les charges latérales);
- Il y a au moins trois rangées de panneaux de portée approximativement égale dans la direction considérée (Nous avons quatre et trois rangées de panneaux dans les deux directions principales);
- La taille de la baie dépasse \(30m^2\) (Notre zone modèle est \(42m^2\)
L'épaisseur choisie pour l'exemple de dalle est supérieure à la valeur minimale maximale de résistance au feu indiquée dans le tableau ci-dessous.
| Résistance au feu standard | Dimensions minimales (mm) | |
|---|---|---|
| Épaisseur de la dalle, hs | Distance d'axe, a | |
| REI 60 | 180 | 15 |
| REI 90 | 200 | 25 |
| REI 120 | 200 | 35 |
| REI 240 | 200 | 50 |
Dans cette section, nous développerons uniquement les calculs pour la direction longitudinale et la bande de colonne (n'hésitez pas à calculer pour une autre direction, la transversale, et pour les bandes intermédiaires). Avant d'approfondir les chiffres, nous devons d'abord diviser en bandes: milieu et colonne. (Pour plus de détails sur les bandes design, consultez cet article SkyCiv: Concevoir des dalles avec ACI-318).
- Largeur de bande de colonne: \(6m/4 = 1.50m\)
- Largeur de la bande médiane: \(7m – 2\times 1.50m = 4.0m\)
EC2 permet d'attribuer des moments dans chaque bande de conception selon le tableau suivant
| Bande de colonne | Bande médiane | |
|---|---|---|
| Moment négatif au bord du poteau | 100% mais pas plus que \(0.17{être}{j^2}{F_{afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués}}\) | 0 |
| Moment négatif à la colonne interne | 60-80% | 40-20% |
| Moment positif dans la portée | 50-70% | 50-30% |
Nous avons sélectionné les pourcentages de moments pour la bande de colonne en cours d'analyse:
- Moment négatif au bord du poteau: 100%.
- Moment négatif à la colonne interne: 80%
- Moment positif dans la portée: 70%
Calcul des moments totaux des bandes de conception:
| Condition de fin de prise en charge | Au premier soutien intérieur | Au milieu des travées intérieures | Aux supports intérieurs | ||||
|---|---|---|---|---|---|---|---|
| Épinglé | Continu | ||||||
| Support extérieur | Près du milieu de la portée d'extrémité | Fin de l'assistance | Portée de fin | ||||
| Moment | 0 | 0.086Floride | – | 0.075Floride | – | 0.063Floride | – |
| 0.04Floride | 0.086Floride | 0.063Floride | |||||
| Tondre | 0.4F | – | – | – | |||
| 0.46F | 0.6F | 0.5F | |||||
Où:
- L est la portée effective
- F est la charge ultime totale dans la travée (1.35Gk + 1.5Qk; Gk est la charge permanente et Qk la surcharge, respectivement)
Il ne sera expliqué qu'un seul cas (support de fin continu) et le reste apparaîtra dans le tableau suivant.
- \(F=Fd\times L = 120.225 \frac{kN}{m} \fois 6m = 721.35 kN \)
- \(M=0.04FL=0.04 \times 721.35 kN \times 6m= -173.124 {kN}{m}\)
- \(d = 280 mm \)
- \(K=\frac{M}{{b}{j^2}{F_{afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués}}}= frac{173.124\fois 10^6 {N}{mm}}{{1500mm}\fois{(280 mm)^ 2}\fois {25 \frac{N}{mm^2}}}=0.012637\)
- \(l_a = 0.95 \)
- \(z=l_a \times d = 0.95\times 280mm = 266.0 mm)
- \(A_s = frac{M}{{0.87}{F_{beurk}}{z}}= frac{173.124\fois 10^6 {N}{mm}}{0.87\fois 500 {N}{mm^2} \fois {266.0mm} = 214.0523 mm^2 }\)
- \(UNE_{s,min}=0,0013{b}{d}=0.0013\times 1500mm \times 280 mm =546 mm^2\)
- \(UNE_{st}=max(Comme, UNE_{s,min}) = maximum(234.83, 546) mm^2 = 299 mm^2 \)
| Des moments | Extérieur négatif gauche | Extérieur positif | Extérieur négatif droit | Intérieur négatif gauche | Positif intérieur | Intérieur Négatif Droit |
|---|---|---|---|---|---|---|
| Valeur M, kN-m | 173.124 | 191.125 | 260.064 | 298.281 | 191.125 | 218.429 |
| K | 0.05897 | 0.06500 | 0.0884 | 0.101 | 0.06500 | 0.0743 |
| z, mm | 266.00 | 266.00 | 266.00 | 266.00 | 266.00 | 266.00 |
| \(Comme, mm^2\) | 1498.366 | 1651.761 | 2247.55 | 2577.835 | 1651.761 | 1887.727 |
| \(UNE_{s,min},mm^2\) | 546.00 | 546.00 | 546.00 | 546.00 | 546.00 | 546.00 |
| \(UNE_{st} {mm^2}\) | 1498.366 | 1651.761 | 2247.55 | 2577.835 | 1651.761 | 1887.727 |
La prochaine étape consiste à calculer l'acier des barres d'armature à l'aide du module de conception de plaques dans SkyCiv. S'il te plaît, continuez à lire la section suivante!
Résultats du module de conception de plaques SkyCiv S3D
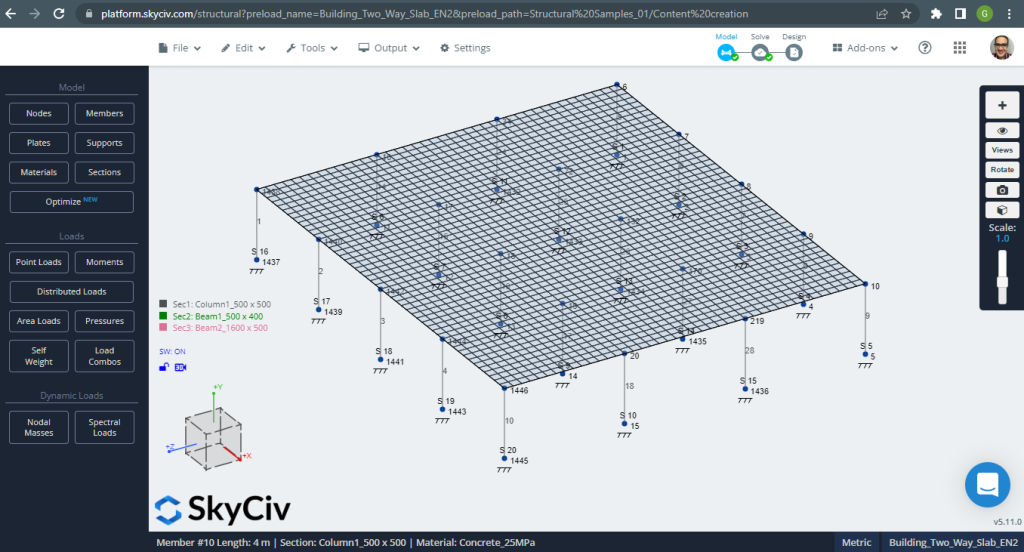
Figure 12. Exemple de dalles unidirectionnelles dans un petit bâtiment. (Structural 3D, Ingénierie Cloud SkyCiv).
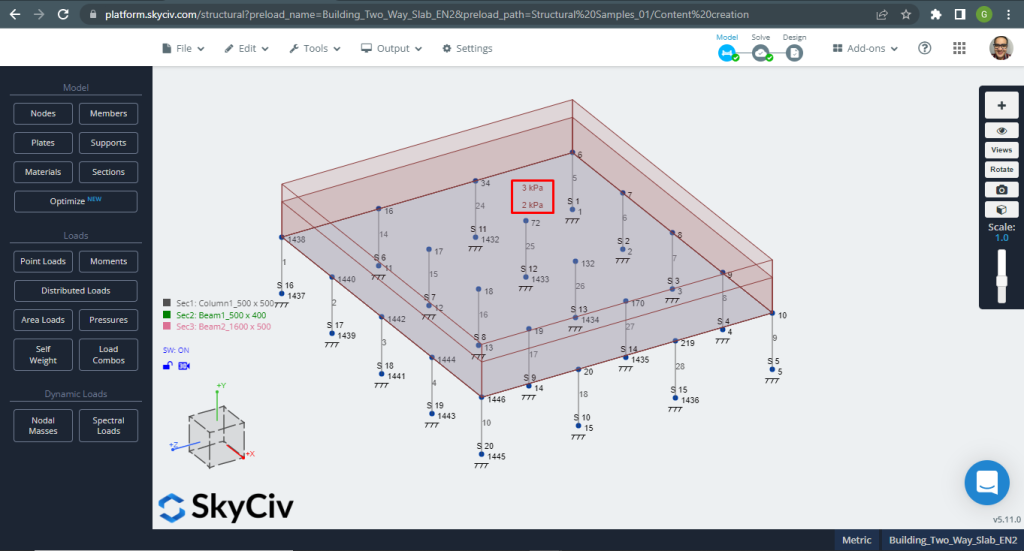
Figure 13. Exemple de dalles unidirectionnelles dans un petit bâtiment. (Structural 3D, Ingénierie Cloud SkyCiv).
Lors de la conception des dalles, nous devons vérifier si le déplacement vertical est inférieur au maximum autorisé par le code. L'Eurocode a établi un déplacement vertical maximal de service de \(\frac{L}{250}= frac{6000mm}{250}=24.0 mm\).
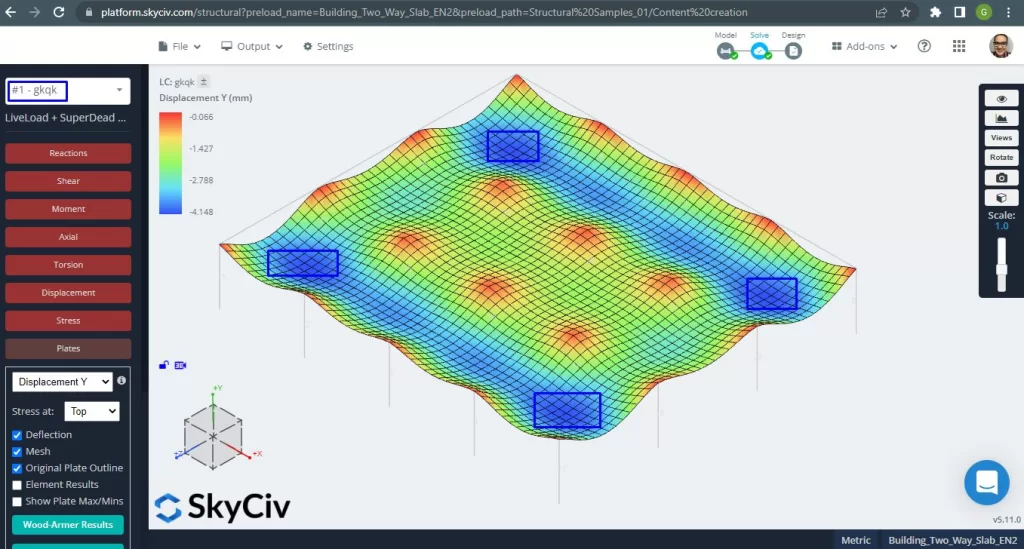
Figure 14. Exemple de dalles unidirectionnelles dans un petit bâtiment. (Structural 3D, Ingénierie Cloud SkyCiv).
L'image ci-dessus nous donne le déplacement vertical. La valeur maximale est de -4,148 mm étant inférieure au maximum autorisé de -24 mm. Par conséquent, la rigidité de la dalle est suffisante.
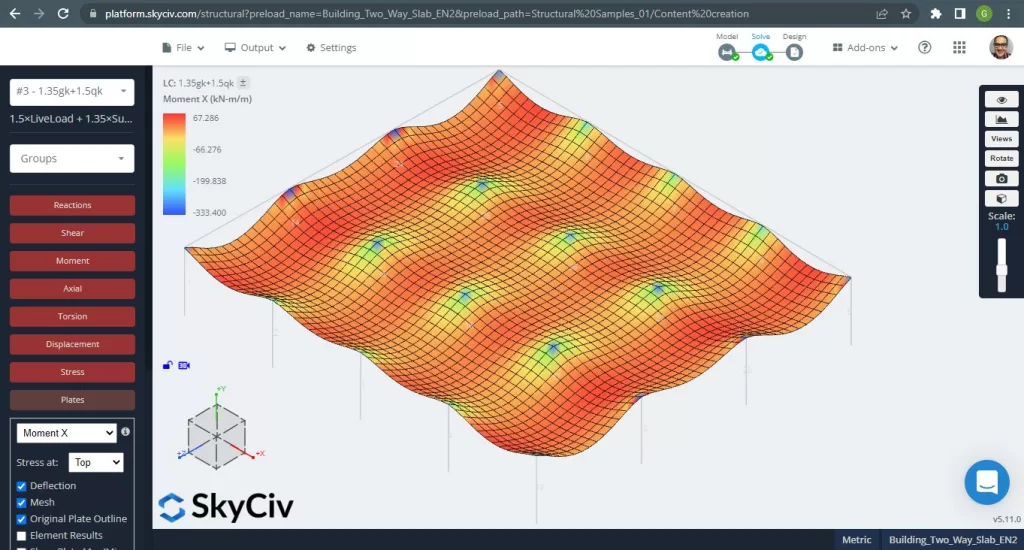
Figure 15. Exemple de dalles unidirectionnelles dans un petit bâtiment. (Structural 3D, Ingénierie Cloud SkyCiv).
Images 15 et 16 se composent du moment de flexion dans chaque direction principale. Prendre la distribution et les valeurs du moment, les logiciels, SkyCiv, peut alors obtenir la surface totale d'armatures en acier.

Figure 16. Exemple de dalles unidirectionnelles dans un petit bâtiment. (Structural 3D, Ingénierie Cloud SkyCiv).
Zones de renfort en acier:
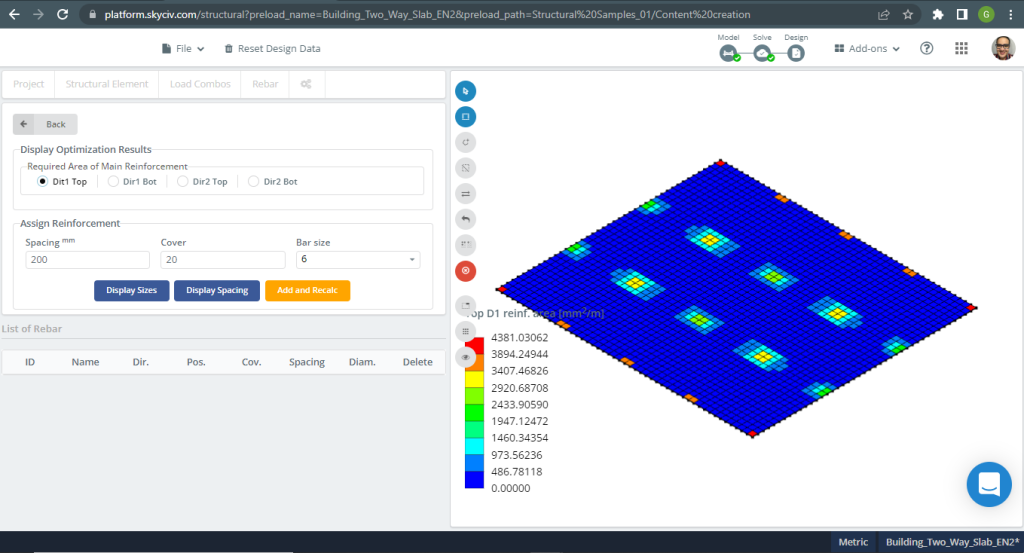
Figure 17. Exemple de dalles unidirectionnelles dans un petit bâtiment. (Structural 3D, Ingénierie Cloud SkyCiv).
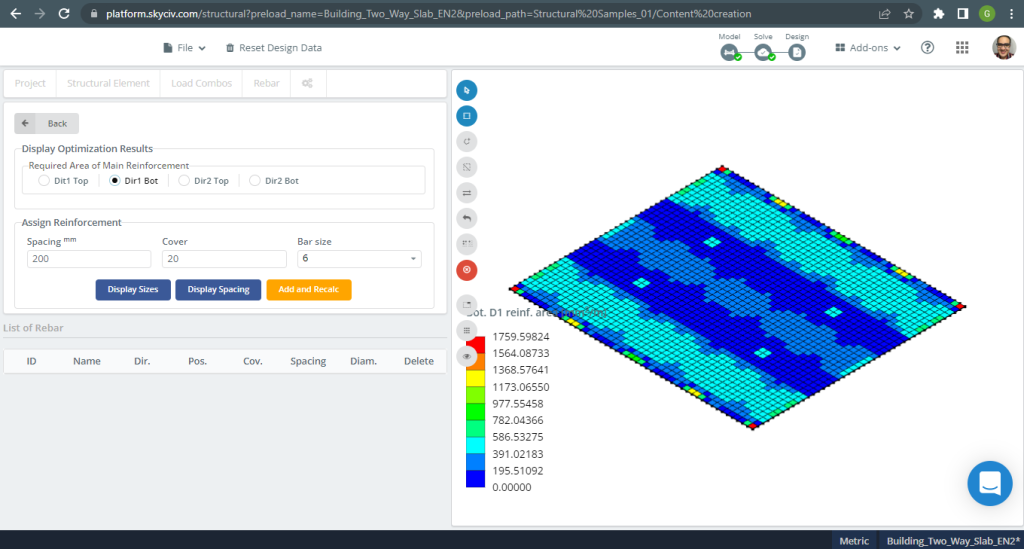
Figure 18. Exemple de dalles unidirectionnelles dans un petit bâtiment. (Structural 3D, Ingénierie Cloud SkyCiv).
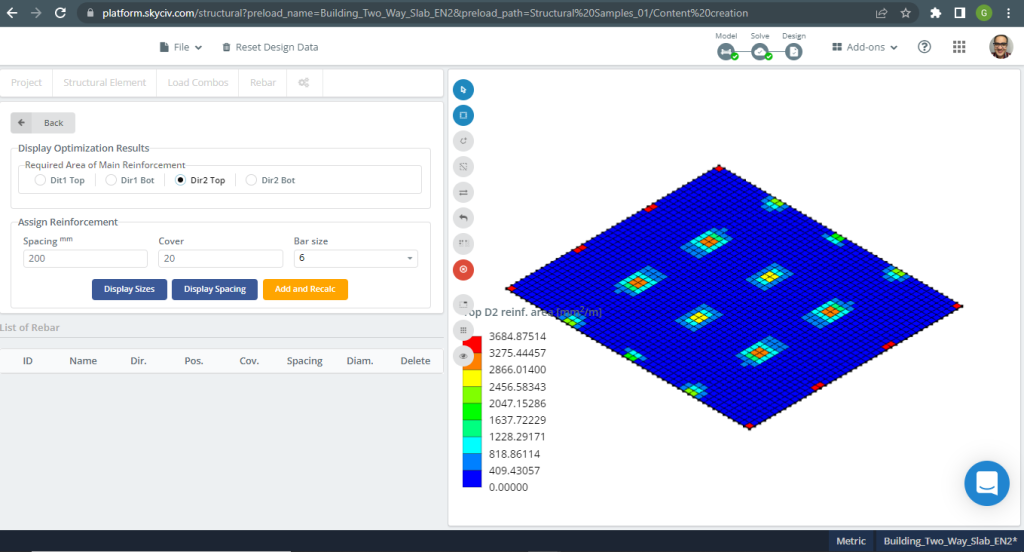
Figure 19. Exemple de dalles unidirectionnelles dans un petit bâtiment. (Structural 3D, Ingénierie Cloud SkyCiv).
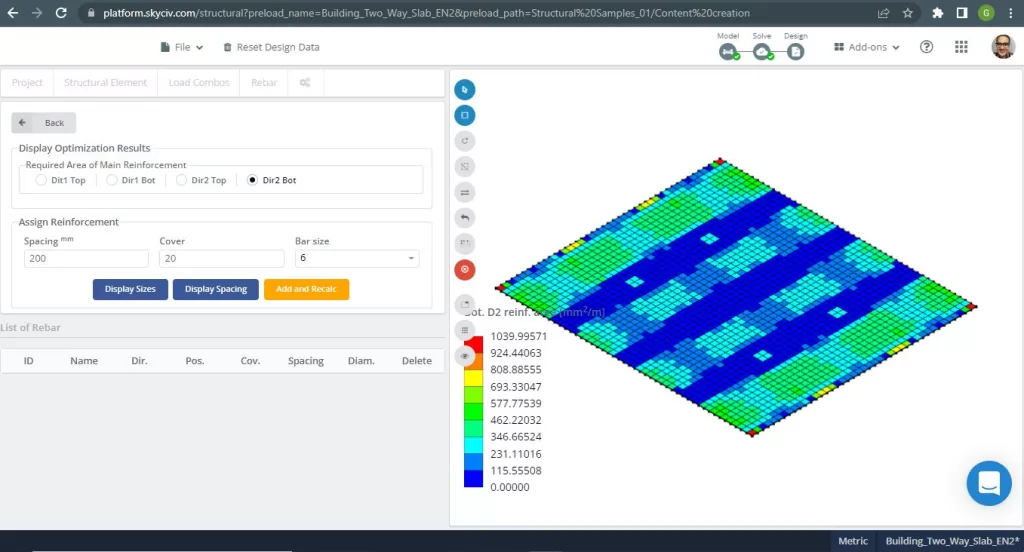
Figure 20. Exemple de dalles unidirectionnelles dans un petit bâtiment. (Structural 3D, Ingénierie Cloud SkyCiv).
Comparaison des résultats
La dernière étape de cet exemple de conception de dalle bidirectionnelle consiste à comparer la surface d'armature en acier obtenue par analyse S3D et calculs manuels..
Acier pour barres d'armature pour la direction X et la bande de colonne
| Moments et zone d'acier | Extérieur négatif gauche | Extérieur positif | Extérieur négatif droit | Intérieur négatif gauche | Positif intérieur | Intérieur Négatif Droit |
|---|---|---|---|---|---|---|
| \(UNE_{st, Calculs manuels} {mm^2}\) | 1498.366 | 1651.761 | 2247.55 | 2577.835 | 1651.761 | 1887.727 |
| \(UNE_{st, S3D} {mm^2}\) | 3889.375 | 1040.00 | 4196.145 | 4196.145 | 520.00 | 3175.00 |
| \(\Delta_{dif}\) (%) | 61.475 | 37.04 | 46.44 | 38.566 | 68.52 | 40.544 |
Si vous êtes nouveau chez SkyCiv, Inscrivez-vous et testez le logiciel vous-même!
Références
- B. Mosley, R. Hulse, JH. Bungey , “Conception du béton armé selon l'Eurocode 2”, Septième édition, Palgrave MacMillan.
- Bazan Enrique & Méli Piralla, “Conception parasismique des structures”, 1ed, CLAIR.
- Eurocode 2: Conception de structures en béton.


