Dans la conception de connexion en acier, boulons sont généralement conçus comme un groupe de boulons qui agiront comme un seul corps pour résister à une charge donnée. La résistance d'un groupe de boulons est généralement calculée par la résistance de contrôle de son boulon le plus critique. Les charges directes sont réparties sur le nombre total de boulons, tandis que le moment induit dû à l'excentricité des charges est distribué en fonction du moment d'inertie du groupe de boulons et de la distance par rapport au centre de gravité. Cette analyse est appelée analyse élastique. En raison de ses hypothèses simplifiées et conservatrices sur la répartition de la charge, il donne souvent des assemblages boulonnés surdimensionnés.
Quand on parle d'ingénierie de la valeur et de conceptions économiques, l'approche inélastique est préférée par la plupart des fabricants. Il nécessite un nombre moindre de boulons pour la même amplitude de charges. Pour faire l'approche inélastique, le centre instantané de rotation (ICOR) méthode utilisant des itérations est la meilleure façon.
Dans cet article, nous montrerons comment calculer la force d'un connexion boulonnée en utilisant la méthode ICOR. Les réactions par boulon seront calculées à l'aide de l'équation (7-1) sur les pages 7-7 de la Manuel AISC 15e édition. Cela sera ensuite utilisé pour vérifier si l'emplacement supposé du centre instantané du groupe de boulons est correct. Ensuite, une fois que nous avons le bon emplacement IC, nous calculerons ensuite le coefficient du groupe de boulons C pour déterminer sa résistance.
L'utilisation de la méthode ICOR pour obtenir le coefficient de groupe de boulons est un long processus car il nécessite une méthode d'essai et d'erreur pour obtenir le centre instantané. (CI) emplacement. De nos jours, avec l'utilisation de solveurs informatiques, l'IC d'un groupe de boulons peut être facilement calculé à l'aide d'itérations programmées. Solveur de groupe SkyCiv Bolt utilise une méthode d'itération rapide pour déterminer l'emplacement du CI et le coefficient de groupe de boulons en quelques secondes. Il est actuellement implémenté dans l'AS 4100 code de conception mais sera bientôt intégré dans le reste des codes de conception.
Obtenir les propriétés du groupe de boulons
Commençons notre analyse simple sur un groupe de boulons de quatre boulons chargés avec une charge de cisaillement verticale excentrique de 10 kips. L'excentricité de la charge le long de l'axe x est 4 pouces à droite du groupe de boulons. L'angle par rapport à la verticale est nul et l'excentricité le long de l'axe y est nulle.
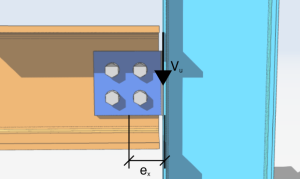
\(V_{u} = 10kips \)
\(\thêta = 0 degré)
\(e_{X} = 4 dans)
\(e_{Y} = 0po)
La première chose à faire est d'obtenir les coordonnées de tous les boulons de notre groupe de boulons. L'utilisation de guides visuels et de tableaux est fortement recommandée.
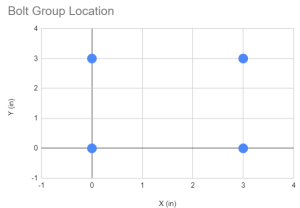
| Identifiant du magasin | X (in) | Y (in) |
| 1 | 0 | 0 |
| 2 | 0 | 3 |
| 3 | 3 | 0 |
| 4 | 3 | 3 |
Pour obtenir le centre de gravité du groupe de boulons le long de x- et axes y, nous avons besoin de la formule ci-dessous.
Laisser \(n \) = nombre total de boulons
\(X_{CG} = frac{\somme X}{n}\)
\(O_{CG} = frac{\somme Y}{n} \)
ensuite, notre solution est:
\(X_{CG} = frac{\somme X}{n} = frac{0 in + 0 in + 3 in + 3 in}{4} = 1.5 dans)
\(O_{CG} = frac{\somme Y}{n} = frac{0 in + 3 in + 0 in + 3 in}{4} = 1.5 dans)
Supposons l'emplacement de l'I.C.
Après avoir obtenu le centroïde, nous supposerons l'emplacement du centre instantané \(CI). Comme un premier essai, nous pouvons supposer que le CI est situé au centre de gravité géométrique du groupe de boulons.
Donc, présumer
\(X_{CI} =X_{CG} = 1.5 dans)
\(O_{CI} = Y_{CG} = 1.5 dans)
ensuite, nous tabulons le déplacement de chaque boulon à l'emplacement de l'IC. Nous pouvons simplement le faire en obtenant d'abord la distance le long de x et la distance le long de y, puis obtenir son déplacement
| Identifiant du magasin | cx (in) | cy (in) | c (in) |
| 1 | -1.5 | -1.5 | 2.121 |
| 2 | -1.5 | 1.5 | 2.121 |
| 3 | 1.5 | -1.5 | 2.121 |
| 4 | 1.5 | 1.5 | 2.121 |
Où,
\(c_{X} =X_{je} – X_{CI}\)
\(c_{Y} = Y_{je} – O_{CI}\)
\(c = sqrt{{\la gauche(c_{X} \droite)}^{2} + {\la gauche(c_{Y} \droite)}^{2}}\)
Pour Boulon Non. 1, notre solution est
\(c_{X} = 0po – 1.5 dans = -1.5 dans)
\(c_{Y} = 0po – 1.5 dans = -1.5 dans)
\(c = sqrt{{\la gauche( -1.5 À droite)}^{2} + {\la gauche( -1.5 À droite)}^{2}} = 2.121in)
Calculer la déformation par boulon par rapport à la distance de IC
par conséquent, après avoir obtenu les distances des boulons à partir de l'emplacement supposé du CI, on calcule ensuite la déformation de chaque boulon en fonction de sa distance.
La déformation maximale par boulon, mis à \(\Delta_{max} = 0.34 dans), est basé sur des données expérimentales pour un boulon ASTM tel que décrit dans la page AISC 7-8. En utilisant la proportion linéaire, et réglage \(\Delta_{max} = 0.34 dans), nous pouvons calculer la déformation d'un boulon individuel par rapport à sa portion à la distance maximale \(c_{max}\). L'équation pour obtenir est montré ci-dessous.
\(\Delta_{1} = 0.34in times left( \frac{c}{c_{max}}\droite) \)
Pour Boulon Non. 1, la déformation est
\(\Delta_{1} = 0.34in times left( \frac{2.121 in}{2.121 in}\droite)\)
Pour le reste des boulons, les déformations calculées sont tabulées ci-dessous.
| Identifiant du magasin | \(\Delta\) (in) |
| 1 | 0.34 |
| 2 | 0.34 |
| 3 | 0.34 |
| 4 | 0.34 |
Obtenez les réactions par boulon
Une fois que nous avons la déformation par boulon, nous pouvons alors utiliser AISC 15th Ed. Eq (7-1) pour obtenir les réactions par boulon.
\(R = R_{ultime} \la gauche ( 1 – e^{-10\Delta}\droite )^{0.55}\)
Ce logiciel \(R_{ultime}\) dans l'équation est la charge ultime supposée sur un boulon, que nous pouvons définir comme la résistance au cisaillement des boulons.
\(R_{ultime} = phi R_{n} \)
Dans notre exemple, nous utiliserons une résistance au cisaillement des boulons de \(24.4 kip). Il est également permis d'utiliser une autre valeur car cela s'annulera simplement lorsque nous calculerons le coefficient de groupe de boulons \(C) plus tard.
Pour Boulon Non. 1, la réaction calculée est
\(R = R_{ultime} \la gauche ( 1 – e^{-10\Delta}\droite )^{0.55}\)
\(R = 24.4 kip gauche ( 1 – e^{-10 \fois gauche ( 0.34 À droite )}\droite )^{0.55}\)
\(R = 23.949 kip)
Pour le reste des boulons, les réactions calculées sont les suivantes. En même temps, les composants de la réaction de boulon \(R) le long de x et y sont également affichés.
| Identifiant du magasin | R (kip) | Rx (kip) | Ry (kip) |
| 1 | 23.949 | 16.937 | -16.937 |
| 2 | 23.949 | -16.937 | 16.937 |
| 3 | 23.949 | 16.937 | -16.937 |
| 4 | 23.949 | -16.937 | 16.937 |
| ⅀Rx = 0 | ⅀Ry = 0 |
Pour Boulon No.1, les solutions pour obtenir les composants x et y sont présentées ci-dessous.
\(R_{X} = -R gauche ( \frac{c_{Y}}{c} \droite ) = -23.949 \fois gauche ( \frac{-1.5in}{2.121in} \droite ) = 23.949 kip)
\(R_{Y} = Rgauche ( \frac{c_{X}}{c} \droite ) = 23.949 \fois gauche ( \frac{1.5in}{2.121in} \droite ) = 23.949 kip)
De plus, nous devrions obtenir le moment de charge induit par boulon en raison de l'excentricité. Pour calculer ce, nous utilisons les composants \(R_{X}\) et \(R_{Y}\) et multipliez-les par les excentricités \(c_{Y}\) et \(c_{X}\), respectivement.
Pour Boulon No.1, le moment de la réaction au CI est
\(M_{r} = -R_{X}c_{Y} + -R_{Y}c_{X} \)
\(M_{r} = -16.937 kip fois gauche ( -1.5À droite) + -16.937 kip fois gauche ( -1.5 À droite ) \)
\(M_{r} = 50.811 poulet-in)
Pour le reste des boulons, les réactions de moment correspondantes sont tabulées ci-dessous.
| Identifiant du magasin | M (poulet dans) |
| 1 | 50.811 |
| 2 | 0 |
| 3 | 0 |
| 4 | 50.811 |
| ⅀Mr = 101.622 |
Vérification de l'emplacement du CI
Maintenant que nous avons les réactions de cisaillement et de moment par boulon, nous l'utiliserons pour déterminer la quantité de charge Pu à laquelle ce groupe de boulons résiste. Pour faire ça, nous obtiendrons la résultante de la somme de toutes les réactions le long de x et de la somme de toutes les réactions le long de y.
De la section précédente, nous avons calculé que
\(\somme R_{X}=0kip\)
et
\(\somme R_{Y}=0kip\)
Donc,
\(P_{u} = sqrt{{\la gauche( \somme R_{X} \droite)}^{2} + {\la gauche( \somme R_{Y} \droite)}^{2}} = 0 kip)
Étant donné que la charge résultante \(P_{u} = 0kip), nous pouvons décider à ce stade de ne pas procéder à la vérification puisque nos données seront simplement nulles. Nous pouvons également en déduire que le premier emplacement présumé d'I.C., qui est au centre de gravité du groupe de boulons, est incorrect. Par contre, aux fins de cette discussion, nous allons procéder avec les étapes ci-dessous.
\(P_{ux} = -P_{u}péchégauche ( \thêta droit ) = 0 kip \)
\(P_{ouais} = -P_{u}cosgauche ( \thêta droit ) = 0 kip \)
\(M_{u} = -P_{ux}\la gauche ( O_{CG} + e_{Y} – O_{CI} \droite ) + -P_{ouais} \la gauche (X_{CG} + e_{X} – X_{CI} \droite ) = 0 kip \)
Puisque,
\(P_{ux} \neq somme R_{X} \)
\(P_{ouais} \neq somme R_{Y} \)
\(M_{u} \je ne suis pas M_{r} \)
Par conséquent, l'emplacement supposé de I.C. est incorrect. Nous pouvons maintenant passer au prochain emplacement supposé.
SkyCiv a une intégration complète du calcul du groupe de boulons dans le module standard australien. Vous voulez essayer notre logiciel de conception de connexion?
Deuxième itération
Pour notre deuxième itération, supposons que le I.C. est situé aux coordonnées indiquées ci-dessous.
Présumer
\(X_{CI} = 0.062 dans)
\(O_{CI} = 1.5 dans)
ensuite, faisons les étapes que nous avons faites dans notre première itération. En résumé, le tableau ci-dessous montrera les coordonnées, la distance de chaque boulon par rapport au CI supposé, et la déformation correspondante par rapport à la distance.
| Identifiant du magasin | X (in) | Y (in) | cx (in) | cy (in) | c (in) | \(\Delta\) (in) |
| 1 | 0 | 0 | -0.062 | -1.5 | 1.501 | 0.155 |
| 2 | 0 | 3 | -0.062 | 1.5 | 1.501 | 0.155 |
| 3 | 3 | 0 | 2.938 | -1.5 | 3.299 | 0.34 |
| 4 | 3 | 3 | 2.938 | 1.5 | 3.299 | 0.34 |
Notez que le centre de gravité calculé du groupe de boulons est toujours le même puisque rien n'a changé sur les coordonnées du boulon.
\(X_{CG} = 1.5 dans)
\(O_{CG} = 1.5 dans)
ensuite, on calcule les réactions selon x, réactions le long de y, et l'instant correspondant. Les valeurs sont tabulées ci-dessous.
| Identifiant du magasin | R (kip) | Rx (kip) | Ry (kip) | M (poulet dans) |
| 1 | 21.4 | 21.4 | -0.9 | 32.1 |
| 2 | 21.4 | -21.4 | -0.9 | 32.1 |
| 3 | 23.9 | 10.9 | 21.3 | 79.0 |
| 4 | 23.9 | -10.9 | 21.3 | 79.0 |
| ⅀Rx = 0 | ⅀Ry = 41 | ⅀Mr = 222 |
Prochain, nous déterminons la charge résultante de toutes les réactions le long de x et y.
\(P_{u} = sqrt{{\la gauche( \somme R_{X} \droite)}^{2} + {\la gauche( \somme R_{Y} \droite)}^{2}}\)
\(P_{u} = sqrt{{\la gauche( 0 kip droit)}^{2} + {\la gauche( 40.703 kip droit)}^{2}}\)
\(P_{u} = 40.703 kip)
ensuite, les composantes de la charge résultante en fonction de la donnée \(\thêta ) est montré ci-dessous.
\(P_{ux} = -P_{u}péché gauche ( \thêta droit ) = -41kip times sin left ( 0 degré droit )= 0 kip)
\(P_{ouais} = -P_{u}car gauche ( \thêta droit ) = -41kip times cos left ( 0 degré droit )= -41 kip)
Nous utiliserons ensuite ces composants pour résoudre pour l'instant la charge autour du I.C supposé.
\(M_{u} = -P_{ux} \la gauche ( O_{CG} + e_{Y} – O_{CI} \droite) + P_{ouais} \la gauche ( X_{CG} + e_{X} – X_{CI} \droite)\)
\(M_{u} = -0 kip gauche ( 1.5 in +0 in – 1.5 À droite) + 41 kip gauche ( 1.5 in +4 in – 0.06 À droite)\)
\(M_{u} = -222 poulet-in)
Prochain, comparons le calcul Pux, Pux, et Mu aux réactions du groupe de boulons.
\(P_{ux} \environ – \somme R_{X}\)
\(P_{ouais} \environ – \somme R_{Y}\)
\(M_{u} \environ – \JE SUIS{u}\)
Puisque le côté gauche est presque égal au côté droit de l'équation, on peut dire que l'emplacement supposé de I.C. est correct!
Résolution du coefficient C
Une fois l'I.C.. l'emplacement est déterminé, nous pouvons maintenant obtenir le coefficient de groupe de boulons C avec la formule ci-dessous.
\(C = frac{P_{u}}{\phi R_{n}} = \frac{40.703 kip}{24.4 kip} = 1.668\)
Calculateur de groupe de boulons gratuit
Vérifiez comment nous concevons nos connexions boulonnées avec cette approche en utilisant notre Calculateur de conception d'assemblages en acier gratuit! Pour plus de fonctionnalité, inscrivez-vous dès aujourd'hui à notre logiciel Structural 3D pour commencer!


