Le moment d'inertie est une propriété géométrique importante utilisée en ingénierie structurelle, puisqu'il est directement lié au montant de des fibres la force de votre section. En général, plus le moment d'inertie est élevé, plus il a de force et moins il fléchira sous la charge. Le moment d'inertie d'un cercle, ou de toute autre forme, est essentiellement le couple nécessaire pour faire tourner la masse autour d'un axe – d’où le terme inertie dans son nom. Remarque, cela ne doit pas être confondu avec la zone de moment d'inertie (Deuxième moment d'inertie) ce qui est un calcul et une valeur tout à fait différents.
Moment d'inertie d'une formule circulaire
Un autre exercice utile consiste à examiner tout cela en considérant la formule générale du cercle du moment d'inertie:
[math] JE_{X}, JE_{Y}[object Window]{\pi}{64}D ^ 4 [math]
Un autre exercice utile consiste à examiner tout cela en considérant le moment général de la formule du cercle d'inertie:
[math] JE_{X}, JE_{Y}[object Window]{\pi}{64}D ^ 4 – \dfrac{\pi}{64}d ^ 4 [math]
Un autre exercice utile consiste à examiner tout cela en considérant le moment général de la formule du cercle d'inertie, Un autre exercice utile consiste à examiner tout cela en considérant le moment général de la formule du cercle d'inertie. Par contre, parce que cela ne fournit pas beaucoup de retenue contre la flexion (Un autre exercice utile consiste à examiner tout cela en considérant le moment général de la formule du cercle d'inertie), Un autre exercice utile consiste à examiner tout cela en considérant le moment général de la formule du cercle d'inertie. Un autre exercice utile consiste à examiner tout cela en considérant le moment général de la formule du cercle d'inertie.
moment d'inertie d'un cercle – Une ventilation détaillée
Le moment d'inertie est important à la fois pour la force/contrainte de moment de flexion et la déflexion. Cela est évident compte tenu de leur formule, où dans les deux cas, I (Moment d'inertie) se trouve au dénominateur:

Source: Formule de contrainte de flexion
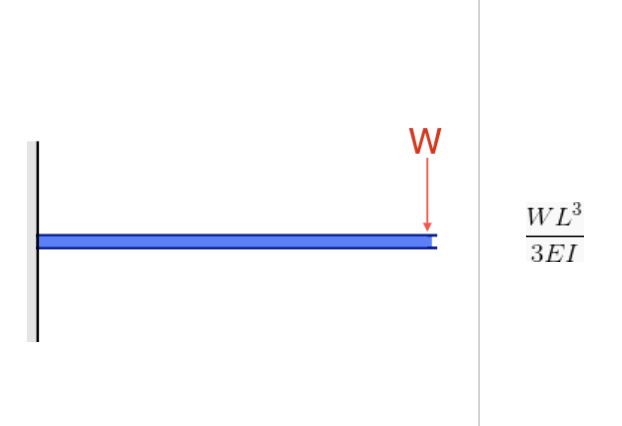
Source: Équation de déviation dans une poutre en porte-à-faux
Le moment d'inertie dans les sections circulaires a un comportement particulier. Tout d'abord, ils ont le même moment d'inertie dans les deux axes (connu sous le nom d'axe majeur et mineur). Cela a du sens car la section est symétrique dans les directions X et Y. Nous verrons comment ce n'est pas toujours le cas dans d'autres les sections, quand on compare avec un faisceau en I ci-dessous. Par contre, cela peut être un avantage lorsque le chargement n'est pas toujours le long de l'axe fort de l'élément, car vous pouvez prédire la résistance de l'élément quelle que soit la direction de la charge. Malgré cela, les sections circulaires n'ont généralement pas de valeurs de moment d'inertie très élevées pour leur poids (par rapport à dire un I beam par exemple) comme nous en apprendrons plus dans la prochaine session.
Avantages et inconvénients des sections circulaires
Il est intéressant de comparer le moment d'inertie d'un cercle par rapport à d'autres formes, pour vraiment comprendre comment il se comporte différemment. Pour un, la majeure partie de la masse est concentrée autour du le centroïde, avec moins de masse en haut et en bas. Ceci est assez important pour les calculs de moment d'inertie, puisque plus la masse s'éloigne, plus la valeur est élevée. Regardons une comparaison, produit par Section Builder de SkyCiv:
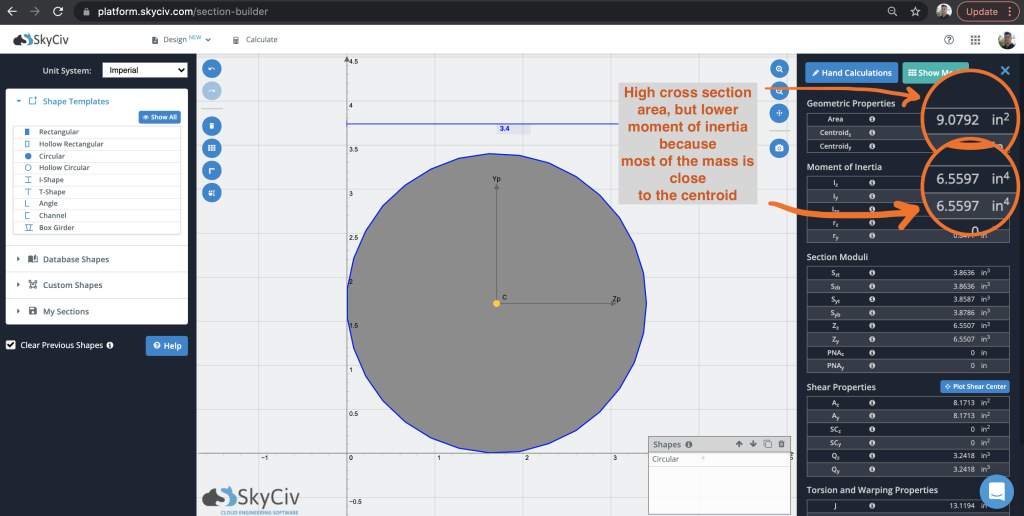
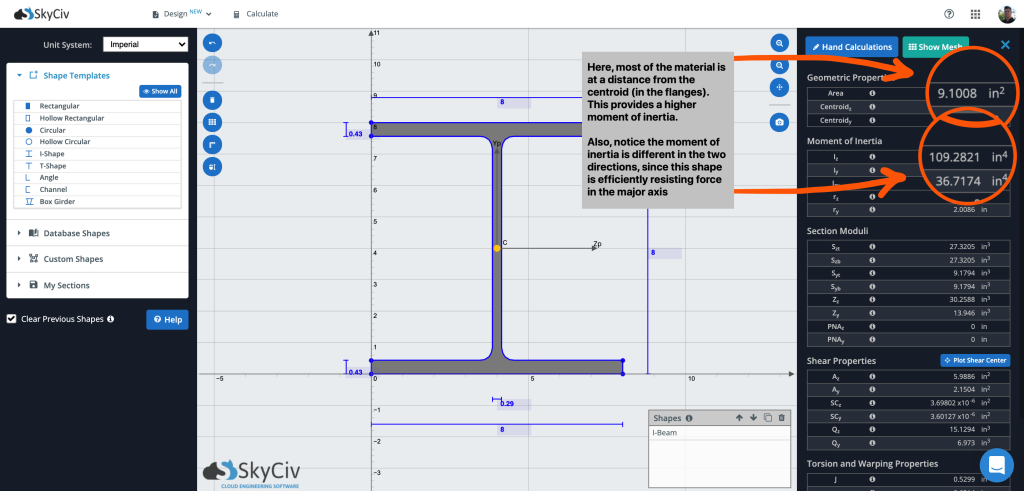
Donc dans ce qui précède, nous avons à peu près 9 pouces carrés de matériau fournissant un moment d'inertie de 6.5597. On voit aussi que les valeurs Iy et Iz sont les mêmes car la section est symétrique dans les deux sens, comme mentionné précédemment. En comparant cela à un I-Beam avec la même zone, nous pouvons voir la différence d'avoir la majeure partie de notre masse plus loin du centre de gravité:
Moment d'inertie d'une section circulaire creuse
Étant donné ce comportement, c'est souvent la raison pour laquelle nous ne voyons pas beaucoup de sections circulaires solides dans l'ingénierie structurelle et sont souvent remplacées par des sections plus favorables Circulaire creuse les sections. Celles-ci sont plus efficaces pour fournir des valeurs de moment d'inertie plus élevées pour la même raison que la poutre en I: la majeure partie de la masse est à distance du centre de gravité. Considérez une forme circulaire creuse avec une zone similaire:
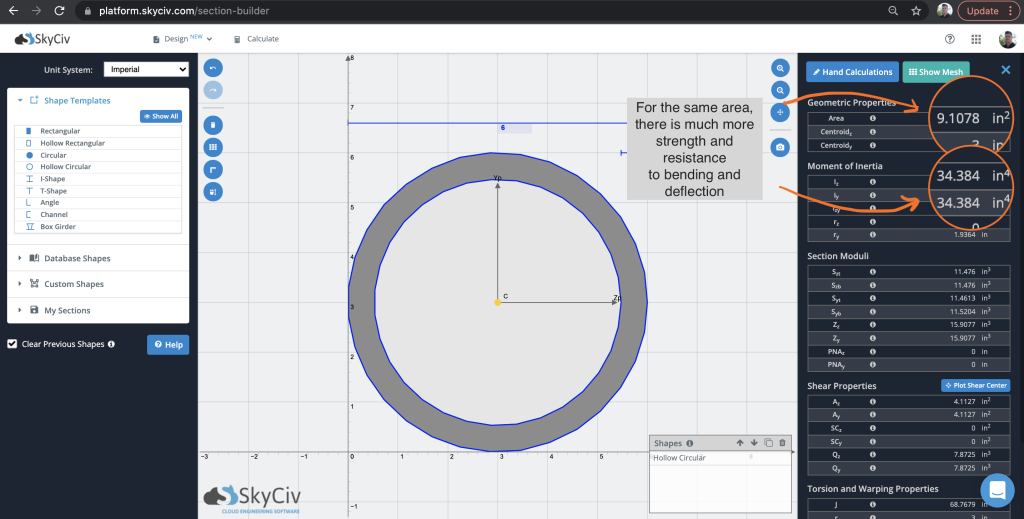
Donc, en résumé pour le même matériau qu'une section circulaire pleine, le moment d'inertie est passé 5 fois plus fort. Cela joue un rôle essentiel dans la résistance au moment de flexion et à la déflexion.
Calculateur de moment d'inertie gratuit
Découvrez notre gratuit Calculateur du moment d'inertie afin que vous puissiez expérimenter avec les calculs ci-dessus. Ou vous pouvez vous inscrire pour commencer avec notre plein Section Builder de SkyCiv version aujourd'hui!


