Calcul du centre de gravité: Un guide simple sur la façon de calculer le centroïde
Le centroïde ou centre de masse des sections de poutre est utile pour l'analyse de poutre lorsque le moment d'inertie est requis pour des calculs tels que le cisaillement/contrainte de flexion et la flèche. Cet article vous guide à travers un processus simple de calcul du centroïde et vous présente le calculateur de centroïde gratuit SkyCiv.
Comment trouver le centroïde
Tout d'abord, vous devez savoir comment trouver le centroïde. Les sections de poutre sont généralement constituées d'une ou plusieurs formes. Donc, pour trouver le centre de gravité d'une zone de section de poutre entière, il doit d'abord être divisé en segments appropriés. Après ça, la zone et le centre de gravité de chaque segment doivent être pris en compte pour trouver le centre de gravité de la section entière.
Comment calculer le centroïde (Équation centroïde):
Considérez la section de poutre en I illustrée ci-dessous. Pour calculer le centre de gravité vertical (dans la direction y) il peut être divisé en 3 segments comme illustré:
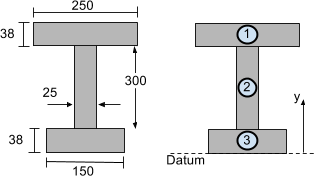
Maintenant, nous devons simplement utiliser l'équation centroïde pour calculer la verticale (Y) d'une section avec plusieurs segments:
Nous prendrons la référence ou la ligne de référence à partir du bas de la section de poutre. Voyons maintenant Aje Andyje pour chaque segment de la section de poutre en I illustrée ci-dessus afin que le centre de gravité vertical ou y puisse être trouvé.
[math]
\texte{Segment 1:}\\
\commencer{aligner}
{A}_{1} &= 250 fois38 = 9500 {\texte{ mm}}^{2}\\
{Y}_{1} &= 38 + 300 + \tfrac{38}{2} = 357 \texte{ mm}\\\\
\fin{aligner}
[math]
[math]
\texte{Segment 2:}\\
\commencer{aligner}
{A}_{2} &= 300 fois25 = 7500 {\texte{ mm}}^{2}\\
{Y}_{2} &= 38 + \tfrac{300}{2} = 188 \texte{ mm}\\\\
\fin{aligner}
[math]
[math]
\texte{Segment 3:}\\
\commencer{aligner}
{A}_{3} &= 38 times150 = 5700 {\texte{ mm}}^{2}\\
{Y}_{3} &= tfrac{38}{2} = 19 texte{ mm}\\\\
\fin{aligner}
[math]
Dans le cas où la section transversale est composée de deux matériaux ou d'un matériau composite, puis l'un des matériaux devra être multiplié par le rapport modulaire de telle sorte que la section entière de l'équation devienne uniforme.
[math]
n = frac{E_{1}}{E_{2}}
[math]
Habituellement, E1 est le module d'élasticité du matériau non dominant, et E2 est le module d'élasticité du matériau dominant, bien que l'ordre préféré n'affecte pas la solution du centroïde. Ajustement pour le deuxième matériau, l'équation centroïde devient la suivante.
[math]
\bar{Y}= frac{\somme{A}_{je}{Y}_{je}+\somme {n}{A}_{je}{Y}_{je}}{\somme{A}_{je}+\somme {n}{A}_{je}}
[math]
Calculer le centroïde du faisceau avec SkyCiv
Le calcul du centroïde du faisceau est important, mais son calcul manuel peut prendre beaucoup de temps.. SkyCiv propose un Calculateur de centroïde gratuit qui automatise ce processus pour vous, vous aider à trouver la verticale (Y) et horizontal (X) centroïdes des sections de poutre facilement et avec précision!
Cet outil est une version gratuite de Générateur de sections SkyCiv, un logiciel complet d'analyse de sections en ligne pour analyser les géométries, la capacité en flexion, propriétés de section de cisaillement et de torsion ainsi que conception FEA et béton armé. Avec cet outil, vous pouvez créer des sections personnalisées à l'aide de modèles prédéfinis ou définir vos propres formes avec des points, lignes, ou importations DXF depuis CAO.
Pour explorer toutes les fonctionnalités Générateur de sections SkyCiv et découvrez la facilité de modélisation et d'analyse de votre section, Inscrivez vous gratuitement aujourd'hui!
Visitez la prochaine étape: Calcul du moment statique / premier moment d'aire.
