Définition de l'analyse fréquentielle?
Lors de la conception de bâtiments, il y en a deux types de charges à envisager: statique et dynamique. Pour le premier, il suffit de calculer la réponse directe de la structure aux charges permanentes appliquées en termes de déplacement et de contraintes. Ceci peut être réalisé en utilisant la méthode de rigidité ou la méthode des éléments finis.
Dans le cas de l'analyse dynamique, il est plus difficile de considérer l'éventail des variations possibles de la réponse de la structure en raison des charges dépendant du temps. Par conséquent, certains nouveaux outils ou fonctions deviennent indispensables à inclure dans l'analyse. Donc, analyse de fréquence, une méthode fondamentale en mécanique vibratoire, se pose.
Cette méthode obtient la variation dans le temps du mouvement de la structure due aux charges dynamiques appliquées. Plus précisement, cela implique d'utiliser les propriétés naturelles de vibration du système structurel pour calculer les efforts internes, déplacements, problèmes de stabilité, etc.
Pour plus d'informations sur le sujet, nous vous suggérons de lire un article SkyCiv qui explique brièvement comment effectuer un Analyse de fréquence dynamique utilisant Logiciel d’analyse structurelle SkyCiv.
Pourquoi l'analyse fréquentielle est-elle pertinente pour la conception?
La meilleure façon de mesurer l'importance de l'analyse fréquentielle dans une conception est de regarder le cas de certaines structures qui ont échoué en raison d'un mauvais comportement dynamique. Un pont célèbre en Amérique du Nord est le Tacoma Narrows, qui s'est finalement effondré après des vibrations périodiques soutenues induites par le vent. Les images suivantes montreront l'augmentation du déplacement le long du pont juste avant l'effondrement, axé principalement sur la chaussée:

Je figure. Vibrations latérales de torsion dans le pont de Tacoma Narrows

Figure ii. Augmentation du déplacement sur le pont avant l'effondrement.

Figure iii. Effondrement catastrophique du pont
Dans cette étude de cas, une analyse de fréquence appropriée n'a pas été effectuée et la structure n'a pas été conçue de manière adéquate pour tenir compte de la fréquence naturelle de la structure.
Pendule simple
L'analyse fréquentielle étudie les différentes formes qu'une structure développe lorsqu'elle est soumise à des actions dynamiques externes. C'est pourquoi vous obtenez plusieurs modes. Puis en utilisant ces formulaires, nous pouvons établir les dimensions des éléments de la structure à travers les efforts internes nécessaires pour garantir l'équilibre.
Avant d'approfondir les considérations techniques et mathématiques pour l'analyse fréquentielle, passez en revue le système simple suivant d'une colonne pendulaire illustré à la figure iv.
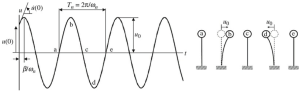
Figure iv. La réponse dynamique d'un système de pendule à vibration libre
En utilisant une analyse simple comme indiqué dans la dernière image, nous pouvons définir le mouvement de la masse supérieure pour la colonne du pendule à chaque fois. L'objectif principal de cet article sera de couvrir l'analyse de fréquence pour deux cas typiques, degrés de liberté simples et multiples.
Degré de liberté unique
Ce cas particulier est le plus simple pour l'analyse dynamique. Le comportement est décrit à l'aide de la loi d'équilibre de D'Alembert, une extension de la deuxième loi de Newton.
La figure suivante montre les éléments du système SDOF, raideur (k), amortissement (c), et source de masse (m) pour les forces d'inertie. La force externe variable dans le temps appliquée sur la masse est représentée par \({p(t)}\).
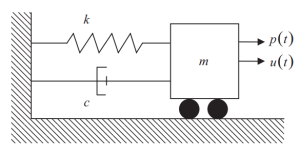
Figure 1. Degré de liberté unique (SDOF) Système. (Bol, 2017, de SkiCiv 56)
Tous les éléments doivent satisfaire la condition d'équilibre dynamique:
\({m}{\point{u}}+{c}{\point{u}}+{k}{u}={p(t)}\)
C'est une équation différentielle linéaire du second ordre, et sa solution a deux composants:
\({u(t)}={u}_{h}(t)+{u}_{p}(t)\)
Où:
- \({u(t)}\) est le déplacement absolu.
- \({u}_{h}(t)\) est la solution homogène, impliquant généralement le cas des vibrations libres.
- \({u}_{p}(t)\) est la solution particulière en fonction de l'excitation appliquée.
Nous nous concentrerons uniquement sur la solution homogène pour décrire le comportement vibratoire et les caractéristiques dynamiques les plus critiques d'une structure..
Définissons les termes suivants:
\({\afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués{n}}={\sqrt(\frac {k}{m})}\) Fréquence angulaire
\({\xi}={\frac{c}{{2}{m}{\oméga_n}}}={\frac{c}{{2}{\sqrt(\frac {k}{m})}}}\) Fraction d'amortissement critique
Lorsque la fraction d'amortissement critique est inférieure à 1, le boîtier de vibration sera sous-amorti; C'est, il y aura des cycles complets avant que le mouvement ne s'arrête.
La solution est de la forme générale suivante
\({euh}={e^{{-\xi}{\afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués{n}}{t}}}{[{A}{cos}{\oméga_d}{t}+{B}{sin}{\oméga_d}{t}]}\)
Où:
- A et B sont des constantes d'intégration qui dépendent des conditions initiales du mouvement.
- \({\oméga_d}={\oméga_n}{\sqrt({{1}-{\xi ^ 2}})}\) est la fréquence angulaire amortie
Une fois l'évaluation des constantes A et B, la solution générale pour le cas non amorti est
\({euh}={e^{{-\xi}{\afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués{n}}{t}}}{[{u_0}{cos}{\oméga_d}{t}+{\frac{{\point{u_0}}+{\xi}{\oméga_n}{u_0}}{\oméga_d}}{sin}{\oméga_d}{t}]}\)
Où:
- \({u_0}\) est le déplacement initial de la masse
- \(\point{u_0}\) est la vitesse initiale de la masse
Si nous traçons la solution avec certaines valeurs des conditions initiales, on obtiendra la figure suivante.
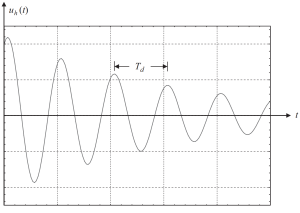
Figure 2. Le déplacement donne une partie homogène de la solution dans un cas amorti sous-critique. (Bol, 2017, de SkiCiv 58)
Dans l'autre cas, il est crucial d'analyser ce qui se passe lorsque la fraction d'amortissement critique a une valeur de 1. \({\xi}=1\). Cette condition implique une structure avec un amortissement complet.
L'équation à utiliser est
\({euh}={e^{{-\afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués{n}}{t}}}{\{u_0+({\point{u_0}}+{\oméga_n}{u_0}){t}}\}\)
Et leur graphique montrant différents cas de conditions initiales est dans l'image suivante.
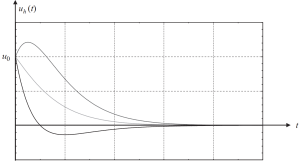
Figure 3. Le déplacement donne une partie homogène de la solution dans un cas fortement amorti. (Bol, 2017, de SkiCiv 58)
Paramètres de réponse
La section précédente nous a aidés à définir la solution pour les vibrations dynamiques libres dans un système SDOF. Les deux principaux paramètres sont la fréquence naturelle \(\omega_n\) qui indique comment la structure va vibrer d'elle-même, et la fraction d'amortissement critique \(\xi\), qui définit la vitesse des vibrations décroissantes.
En général, les structures ont un faible amortissement avec une valeur maximale de \(\xi\)=10 %. Si nous évaluons la fréquence propre amortie en utilisant cette valeur, le résultat est \({\oméga_d}=0,995{\oméga_n}\). Donc, il est recommandé d'utiliser \({\oméga_d}{\épais environ}{\oméga_n}\).
Nous pouvons résumer les propriétés dynamiques dans le tableau suivant.
| Fréquence angulaire (radio/s) | Fréquence naturelle (Hz) | Période naturelle (s) | |
|---|---|---|---|
| Fréquence angulaire \({\oméga_n}\) | \({\oméga_n}\) | \(2{\pi}{f_n}\) | \(\frac{2{\pi}}{T_n}\) |
| Fréquence naturelle \({f_n}\) | \(\frac{\oméga_n}{2{\pi}}\) | \(f_n\) | \(\frac{1}{T_n}\) |
| Période naturelle \({T_n}\) | \(\frac{2{\pi}}{\oméga_n}\) | \(\frac{1}{f_n}\) | \(T_n\) |
Le tableau 1. Relation entre la fréquence angulaire, fréquence naturelle, et période (Bol, 2017, de SkiCiv 60)
Plusieurs degrés de liberté
Lorsque plusieurs masses existent dans une structure, nous devons définir plusieurs coordonnées pour décrire la position à tout moment pour ces masses. Un exemple particulier et évident est illustré dans la figure suivante, consistant en un pendule complexe où différents angles sont nécessaires pour établir la position à chaque instant du mouvement.
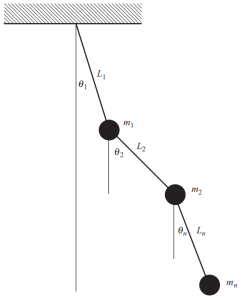
Figure 4. Pendule à masses multiples. (Bol, 2017, de SkiCiv 53)
Dans cette section, nous analysons les structures’ réponse dynamique générale utilisant l'extension de l'analyse de fréquence des propriétés pour plusieurs degrés de liberté.
Il est impératif d'être conscient du processus de modélisation lorsqu'il s'agit d'une structure réelle. Les images suivantes décrivent les étapes nécessaires pour construire un modèle mathématique prêt à appliquer l'analyse de fréquence pour décrire sa réponse dynamique.
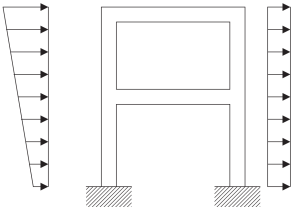
Figure 5. Modèle physique d'un cadre structurel continu. (Bol, 2017, de SkiCiv 23)
La première étape consiste à regrouper les masses à chaque niveau d'intersection des poutres et des poteaux. Chaque nœud a trois mouvements possibles, deux déplacements linéaires, et un tour. Pour être cohérent dans l'analyse, les masses et les propriétés inertielles polaires doivent être prises en compte.
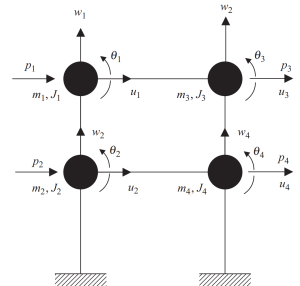
Figure 6. Masses localisées aux nœuds avec degrés de liberté de déplacement et de rotation. Système discret. (Bol, 2017, de SkiCiv 23)
La méthode de condensation statique peut aider à réduire la complexité de l'analyse, négliger l'inertie de rotation et de translation.
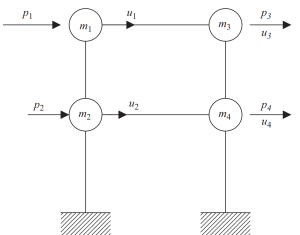
Figure 7. Condensation statique du degré de liberté au seul déplacement horizontal. (Bol, 2017, de SkiCiv 23)
Dans la dernière étape, nous pouvons regrouper en seulement deux nœuds le mouvement horizontal pour cet exemple de cadre.
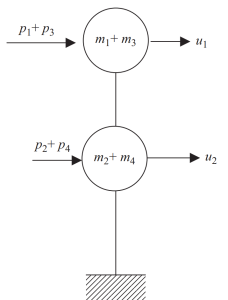
Figure 8. Condensation statique finale à deux nœuds et degré de liberté de déplacement horizontal. (Bol, 2017, de SkiCiv 24)
Comme nous l'avons fait dans la section précédente avec le système SDOF, nous développerons la solution de l'équation de mouvement pour plusieurs degrés de liberté.
L'équation de mouvement s'écrit sous forme matricielle comme
\([M]\{\point{u}\} + [C]\{\point{u}\}+[K]\{u\}={p(t)}\)
Où:
- \([M]\) est la matrice de masse
- \([C]\) est la matrice d'amortissement de Coulumb
- \([K]\) est le matrice de rigidité
Nous devons étudier la solution de vibration libre pour obtenir les paramètres de réponse. Il n'y a pas d'amortissement et de force appliquée au système, seules les conditions initiales à évaluer.
\([M]\{\point{u}\} +[K]\{u\}={0}\)
Par analogie avec le premier cas pour un SDOF, on peut tester une solution sinusoïdale de la forme.
\({u(t)}={\phi}{({a}{cos}{\oméga}{t}+{b}{sin}{\oméga}{t})}\)
\({\point{u}{(t)}}={-{\oméga}^ 2}{\phi}{({a}{cos}{\oméga}{t}+{b}{sin}{\oméga}{t})}\)
dans lequel le vecteur \(\phi\) est un vecteur de forme qui ne dépend pas du temps. Les coefficients “a” et “b” sont des constantes obtenues lors de l'évaluation des conditions initiales.
Après avoir remplacé les deux expressions pour la solution de test dans l'équation de mouvement, on obtient le problème linéaire valeur propre-vecteur propre:
\([K]{\phi}={{\oméga}^ 2}[M]{\phi}\)
Où:
- \({{\oméga}^ 2}\) est l'ensemble des valeurs propres
- \({\phi}\) est l'ensemble des vecteurs propres
La solution à ce problème classique pour l'exemple de cadre dans les dernières figures montre comment les masses vont vibrer. Cela signifie que chaque masse se déplacera dans une direction horizontale en fonction de la valeur des vecteurs propres.
Regardez l'image suivante de ce comportement.
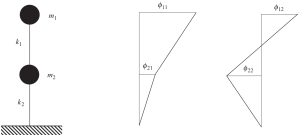
Chiffre n ° 9. Analyse de fréquence montrant les résultats des deux vecteurs propres. (Bol, 2017, Page 135)
SkyCiv Structural 3D
Effectuez une analyse fréquentielle de vos structures avec SkyCiv Structural 3D. Inscrivez-vous aujourd'hui pour commencer!
Références:
- Eduardo Kausel, (2017). “Dynamique structurelle avancée” 1première édition, la presse de l'Universite de Cambridge


