Comment calculer une poutre indéterminée – Méthode double intégrale

Indéterminé poutres peut être un défi en raison des étapes supplémentaires nécessaires pour résoudre les réactions. Rappelez-vous que les structures indéterminées ont ce qu'on appelle un degré d'indétermination. Pour résoudre la structure, des conditions aux limites doivent être introduites. par conséquent, plus le degré d'indétermination est élevé, plus les conditions aux limites doivent être identifiées. Mais avant de pouvoir résoudre un faisceau indéterminé, il faut d'abord identifier si le faisceau est statiquement indéterminé. Comme les poutres sont des structures unidimensionnelles, l'utilisation de l'équation pour déterminer des structures externes statiquement indéterminées est suffisante.

[math]
je_{e}= R- gauche ( 3+e_{c} \droite )
[math]

Où:

• je_e = Degré d'indétermination
• R = nombre total de réactions
• e_c = Conditions externes (par exemple. charnière interne)

Habituellement, toutefois, sans avoir besoin de résoudre le degré d'indétermination, tout autre élément que de simples travées ou des poutres en porte-à-faux est statiquement indéterminé, en supposant que ces poutres ne sont pas livrées avec des charnières internes.

Il existe de nombreuses façons d'aborder la résolution de faisceaux indéterminés. Bien que par souci de simplicité et de similitude avec SkyCiv Beam calculs manuels, nous discuterons de la méthode Double Intégration.

Double intégration

La double intégration est peut-être la plus simple de toutes les méthodes d'analyse des poutres. Le concept de cette méthode est assez simple par opposition à d'autres méthodes car il repose principalement sur une compréhension de base du calcul intégral, d'où la désignation. Un peu de calcul intégral est adapté de la relation de la courbure de la poutre au moment qui est montré ci-dessous.

[math]
\frac{1}{\rho}= frac{M}{NON}
[math]

Notez que 1 / ρ est la courbure de la poutre et que ρ est le rayon de la courbe. Fondamentalement, la définition de la courbure est le taux de changement de la tangente par rapport à la longueur de l'arc. Comme le moment est fonction du chargement par rapport à la longueur de l'élément, l'intégration de la courbure par rapport à la longueur de l'élément donnera la pente de la poutre. De manière similaire, l'intégration de la pente par rapport à la longueur de l'élément donnera la flèche de la poutre. Les chargements structurels typiques étant de nature algébrique, l'intégration de ces expressions est aussi simple que d'utiliser la formule de puissance générale.

[math]
\int f gauche ( x droite )^{n}dx = frac{f gauche ( x droite )^{n + 1}}{n + 1}+C
[math]

La meilleure façon de comprendre le concept est peut-être de fournir un exemple de poutre avec les éléments suivants.

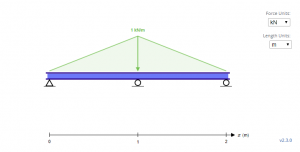
Le faisceau échantillon ci-dessus est un faisceau indéterminé avec des chargements triangulaires. Avec le les appuis, A_Y, B_Y et C_Y pour le premier, deuxième, et troisième supports respectivement, la première étape pour résoudre ces inconnues est de commencer par les équations d'équilibre.

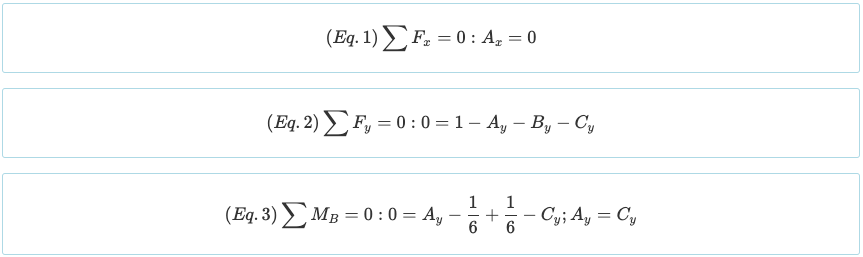
Notez que le faisceau a un degré de indétermination statique de 1°. Comme il y a quatre inconnues (A_X, A_Y, B_Y, et C_Y) et il y a trois équations si loin des équations d'équilibre ci-dessus, il est nécessaire de créer une autre équation à partir des conditions aux limites. Rappelons que les moments générés par une charge ponctuelle et une charge triangulaire sont les suivants.

Charge ponctuelle:

[math]
M = F fois x; M = Fx
[math]

Charge triangulaire:

[math]
M = frac{w_{0}\fois x}{2}\fois gauche ( \frac{X}{3} \droite ); M = frac{w_{0}x ^{2}}{6}
[math]

En utilisant la méthode de double intégration, ces nouvelles équations sont faites et affichées ci-dessous.

Remarque: Les équations ci-dessus sont écrites comme des fonctions de Macaulay où une expression est égale à zéro lorsque X < L. Dans le cas présent, L = 1.

Dans les équations ci-dessus, remarquez que le quatrième terme ajouté semble sortir de nulle part. En réalité, la direction du chargement est opposée à la direction de la gravité. Cela est dû au fait que les équations pour les chargements triangulaires ne fonctionnent que lorsque la charge est ascendante à mesure que la longueur augmente. Ce n'est pas vraiment un problème pour les équations de distribué et charges ponctuelles en raison de leur symétrie. En effet, le chargement équivalent pour la poutre ci-dessus ressemble à la poutre ci-dessous, ainsi les équations sont basées dessus.

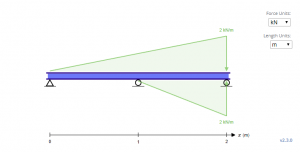
Pour résoudre C₁ et C₂, les conditions aux limites doivent être déterminées. Dans le faisceau ci-dessus, on peut observer que trois de ces conditions aux limites existent à X = 0, X = 1, et X = 2, où la déflexion y est nulle aux trois emplacements.

Condition limite 1

[math]
x = 0, y = 0; C_{2}= 0
[math]

Condition limite 2

[math]
x = 0, y = 0; C_{1}= frac{1}{120}-\frac{UNE_{Y}}{6}
[math]

Après avoir déterminé les valeurs de chaque constante, la dernière équation peut maintenant être obtenue en utilisant la dernière condition aux limites.

Condition limite 3

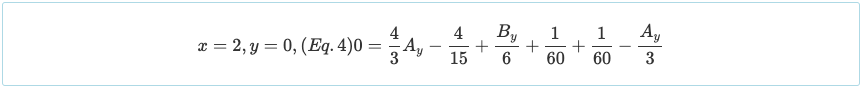
Notez que la condition aux limites de θ = 0 à x = 1 peut être utilisé, bien qu'il ne soit applicable que pour la réaction médiane d'une poutre continue symétrique à chargement symétrique.

Comme les quatre équations ont été déterminées, ils peuvent maintenant être résolus simultanément. La résolution de ces équations donnera les réactions suivantes.

Avec les réactions déterminées, les valeurs des réactions peuvent être remplacées par l'équation du moment. Cela nous permettra de déterminer la valeur du moment dans n'importe quelle partie du système de poutre.

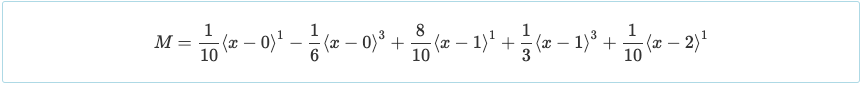
Une autre commodité de la double intégration est que l'équation du moment est présentée d'une manière qui peut être utilisée pour résoudre le cisaillement avec la relation indiquée ci-dessous.

[math]
V = frac{dM}{dx}
[math]

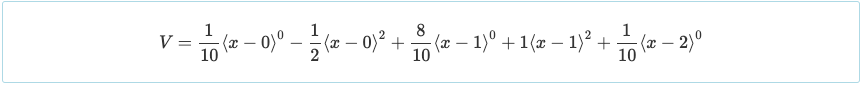
Encore une fois, en utilisant uniquement une compréhension de base du calcul différentiel, assimiler la dérivée d'une fonction à zéro donne le maximum ou le minimum de cette fonction. C'est à dire, équivaut à V = 0 se traduira par un moment positif maximum à X = 0.447 et X = 1.553 de M = 0.030

Bien sûr, tout cela peut être vérifié avec SkyCiv Beam.

Logiciel SkyCiv Beam

Le logiciel d'analyse de poutre SkyCiv permet aux utilisateurs d'analyser facilement et avec précision les structures de poutres. Vous pouvez obtenir une analyse de votre élément de poutre, notamment réactions, les efforts tranchants, moments de flexion, la flèche, et la contrainte interne dans quelques secondes.

Si vous voulez d'abord une période d'essai, Calculateur de poutre gratuit est une excellente façon de débuter, ou inscrivez-vous simplement gratuitement aujourd'hui!