Table des matières
- Types de supports et leurs réactions
- Un guide étape par étape pour déterminer les réactions de support dans les poutres
- Logiciel SkyCiv Beam
Types de supports et leurs réactions
Première, il est important de comprendre également les différents types de supports et les réactions qu'ils produisent dans votre modèle d'analyse. Vous trouverez ci-dessous une courte feuille de triche des différents types de support et de leurs réactions:
| Type de soutien | Traduction | Rotation | Remarques |
|---|---|---|---|
L'appui fixe |
Fixé dans toutes les directions Réactions en X,Y,Z |
Fixé dans toutes les directions Réactions en X,Y,Z |
FFFFFF – Réactions à tous les degrés de liberté |
Support de rouleau horizontal |
Fixé en Y Réactions dans la direction Y uniquement |
Lâché dans toutes les directions Pas de réactions de rotation |
RFFRRR – Les réactions sont uniquement dans la direction Y |
Support goupillé ou articulé |
Fixé en X,Y,Z Réactions en X,Y,Z |
Lâché dans toutes les directions Pas de réactions de rotation |
FFFRRR – Réactions dans toutes les traductions, aucun en rotation |
Support en porte-à-faux |
Fixé dans toutes les directions Réactions en X,Y,Z |
Fixé dans toutes les directions Réactions en X,Y,Z |
Identique au fixe |
Un guide étape par étape pour déterminer les réactions de support dans les poutres:
La détermination des réactions au niveau des supports est toujours la première étape de l'analyse d'une structure de poutre, et c'est généralement le plus simple. Il s'agit de calculer à la fois la formule de la force de réaction et les moments de réaction au niveau des supports. (prend en charge A et B dans l'exemple ci-dessous) en raison des forces agissant sur la poutre. La formule de la force de réaction est utilisée pour trouver les forces exercées sur les supports en raison des charges agissant sur la poutre.. Vous aurez besoin de le savoir pour progresser et calculer diagrammes des moments fléchissants (BMD) et diagrammes de force de cisaillement (SFD); une partie importante de vos cours de statique et de structure collégiale / universitaire. SkyCiv offre un puissant Calculateur de réaction gratuit qui vous permet de modéliser n'importe quelle poutre et de montrer ces calculs manuels pour vous, mais c'est aussi un concept important à comprendre.
Didacticiel vidéo: Déterminer les réactions aux appuis
Lors de la résolution d'un problème comme celui-ci, nous voulons d'abord nous rappeler que le faisceau est statique; ce qui signifie qu'il ne bouge pas. De la physique simple, cela signifie que la somme des forces dans la direction y est égale à zéro (e.g. le total des forces vers le bas est égal au total des forces vers le haut). Une deuxième formule à retenir est que la somme des moments autour d'un point donné est égale à zéro. C'est parce que le faisceau est statique et donc ne tourne pas.
Déterminer les réactions aux appuis, suivez ces étapes simples:
1. Somme des instants (ΣM = 0)
Tout ce que nous devons savoir sur les moments à ce stade, c'est qu'ils sont égaux à la force multipliée par la distance d'un point (e.g. la force x distance d'un point). Prenons un exemple simple de poutre de 4 m avec un support de goupille en A et un support de rouleau en B. Le diagramme du corps libre est illustré ci-dessous où AY et BY sont les réactions verticales aux supports: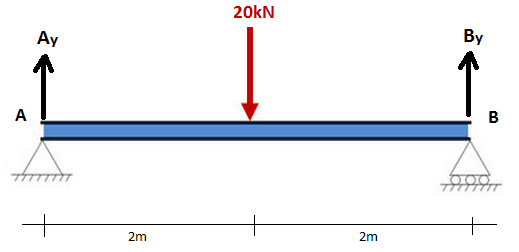
Nous voulons d'abord considérer la somme des moments autour du point B et la laisser égale à zéro. Nous avons choisi le point B pour prouver que cela peut être fait à chaque extrémité de la poutre (à condition qu'il soit pris en charge par la broche). Par contre, vous pouvez tout aussi bien travailler à partir du point A. Donc, maintenant nous additionnons les moments autour du point B et laissons la somme égale 0:
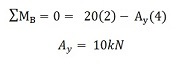
REMARQUE: La convention de signe que nous avons choisie est que les moments dans le sens anti-horaire sont positifs et les moments dans le sens horaire sont négatifs. C'est la convention de signe la plus courante mais c'est à vous. Vous devez TOUJOURS utiliser la même convention de signe tout au long du problème. Utilisez toujours la même convention de signe depuis le début. Nous avons maintenant notre première équation. Nous devons résoudre une autre équation pour trouver BY (la force de réaction verticale au support B).
2. Somme des forces horizontales (ΣFY = 0)
Somme les forces dans le y (vertical) direction et laissez la somme égale à zéro. N'oubliez pas d'inclure toutes les forces, y compris les réactions et les charges normales telles que les charges ponctuelles. Donc, si nous additionnons les forces dans la direction y pour l'exemple ci-dessus, on obtient l'équation suivante:
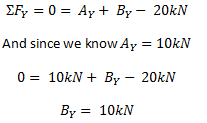
REMARQUE: Encore une fois, nous nous sommes tenus à une convention de signe qui devait prendre des forces ascendantes (nos réactions) comme forces positives et descendantes (la charge ponctuelle) comme négatif. N'oubliez pas que la convention de signe dépend de vous, mais vous devez TOUJOURS utiliser la même convention de signe tout au long du problème.
Alors là nous l'avons, nous avons utilisé les deux équations ci-dessus (la somme des moments est égale à zéro et la somme des forces verticales est égale à zéro) et calculé que la réaction au support A est 10 kN et la réaction au support B 10kN. Cela a du sens car la charge ponctuelle est juste au milieu de la poutre, ce qui signifie que les deux supports doivent avoir les mêmes forces verticales (e.g. c'est symétrique).
Lors de la détermination des forces agissant sur la poutre, la somme des forces et la somme des moments sont utilisées. La formule de la force de réaction permet de calculer les forces verticales et horizontales, tout en additionnant les moments de réaction, vous pouvez garantir que la poutre reste en équilibre statique.
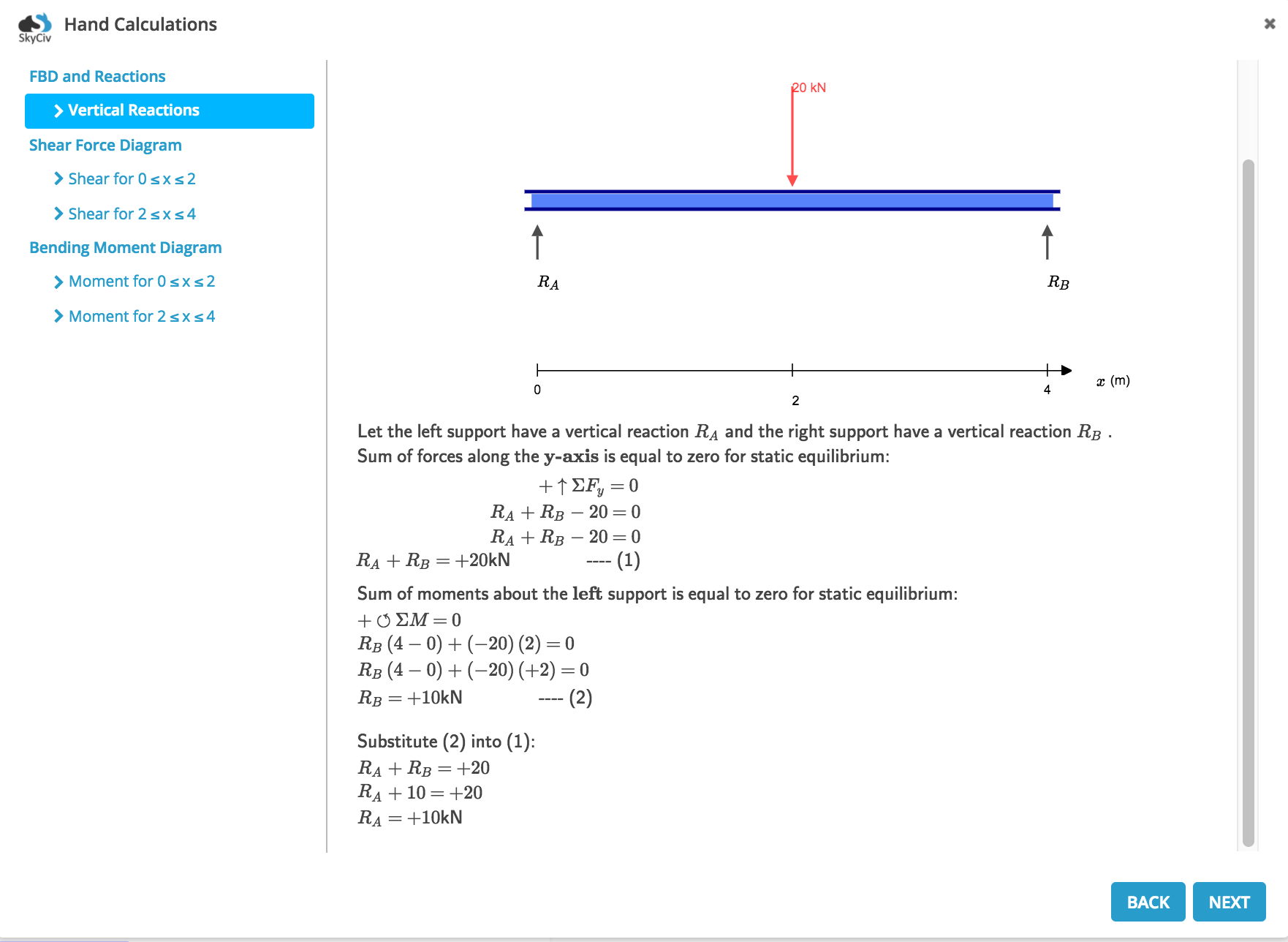
En résumé, voici le plein calculs manuels produit par SkyCiv Beam:
Logiciel SkyCiv Beam
À l'aide de cet article, vous avez appris à trouver la force de réaction. Le logiciel d'analyse de poutre SkyCiv permet aux utilisateurs d'analyser facilement et avec précision les structures de poutres. Vous pouvez obtenir une analyse de votre élément de poutre, y compris les réactions d'appui, les efforts tranchants, moments de flexion, la flèche, la contrainte interne, et poutres indéterminées dans quelques secondes.
Si vous voulez d'abord une période d'essai, Calculateur de poutre gratuit est une excellente façon de débuter, ou inscrivez-vous simplement gratuitement aujourd'hui!