MATÉRIAUX ORTHOTROPES
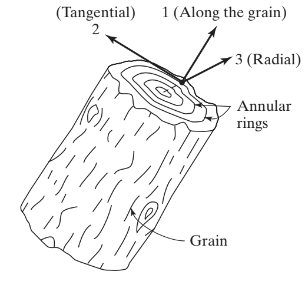
Avant de passer par une explication des plaques orthotropes, regardons quelques exemples de matériaux orthotropes. Des matériaux tels que les cristaux de topaze et de barytine sont orthotropes (Chandrupatla, 2012). Un autre matériau orthotrope très courant est le bois. Figure 1 montre les axes principaux dans lesquels les propriétés mécaniques sont définies pour le bois.
Figure 1. Le bois comme matériau orthotrope (Chandrupatla & Belegundu ,2012, de SkiCiv 233)
des Y 1 est défini le long du grain ou des fibres; de cet axe 2 est tangentiel et axe 3 fonctionne radialement. La loi de Hooke généralisée pour cet exemple (et pour tout autre matériau orthotrope) peut être écrit comme
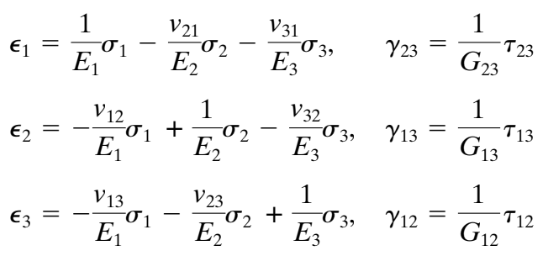
Équations 1. Loi de Hooke généralisée (Chandrupatla & Belegundu,2012, de SkiCiv 233)
Où:
- e1, e2, e3 sont les souches normales.
- c12, c13, c23 sont les déformations de cisaillement.
- E1, E2, et E3 sont les modules de Young le long de l'axe principal.
- g12, g13, g23 sont le module de cisaillement.
- n21, n31, n12, n32, n23 sont les coefficients de Poisson.
- Pour les indices combinés, le premier chiffre indique où la contrainte est appliquée et le second où se produit la déformation.
Par conséquent, la principale différence dans un matériau orthotrope est que nous avons des propriétés mécaniques différentes le long des axes principaux, C'est, “X”, “Y”, “z”.
PLAQUES ORTHOTROPES
Il existe des cas d'utilisation courants pour plaques en génie des structures, que nous pouvons résumer comme suit: plat isotrope, composite ou sandwich et raidi (W. Jiang et al, 1997).
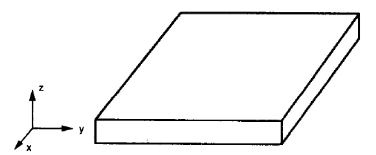
Les plaques planes isotropes sont des plaques régulières (figure n°2), il suffit de définir une valeur pour le coefficient de Poisson, Jeune, et le module de cisaillement car les propriétés mécaniques dans toutes les directions ne changent pas.
Figure n°2. Les plaques plates sont généralement isotropes (W. Jiang et al, 1997, de SkiCiv 106)
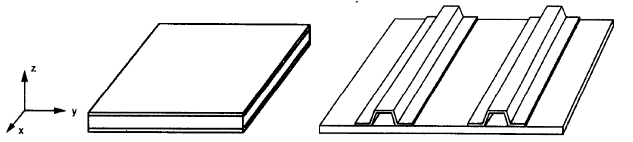
Pour les deux dernières options, plaques sandwich et raidies (figure n°3), il faut définir différentes propriétés mécaniques dans leur axe principal. Ces différentes valeurs rendent les plaques orthotropes.
Figure 3. Composite (la gauche) et plaques raidies chapeau (droite) (W. Jiang et al, 1997, de SkiCiv 106)
Dans une plaque orthotrope, on aurait deux axes avec la même raideur, figure n°3. Les axes "x" et "y" reposent sur un plan, et "z" lui est perpendiculaire.
On peut dire ça (W. Jiang et al, 1997):
- EX = EY ≠ Ez ; (EX, EY )> Ez .
- nxz =nyz ≠nxy ; (nxz, nyz) >nxy
- gxy = gxz = gyz
Les expressions indiquées précédemment impliquent que la rigidité dans les directions "x" et "y" est supérieure à "z". Les coefficients de Poisson montrent également qu'il y a plus de déformation dans les plans liés à la direction "z" que dans un plan formé par les axes "x" et "y"..
EXEMPLE
Description et mise en place
Pour résumer les concepts appris dans les sections précédentes, nous allons développer un exemple dans SkyCiv. Il consiste en l'analyse d'un panneau sandwich mur/dalle qui est construit avec deux couches de béton projeté séparées par une âme en polystyrène. Nous avons choisi la référence suivante pour les propriétés mécaniques à utiliser dans la modélisation: Torres Villavicencio et al. (2013).

Figure 4. Panneau sandwich mur/dalle
Pour capturer la différence d'analyse dans les plaques lorsque nous sélectionnons les options avancées (orthotrope), nous développons une courte comparaison des panneaux sandwich décrits ci-dessus et une approximation de leurs propriétés mécaniques en utilisant une approche isotrope. Le dernier cas utilise des valeurs de propriétés mécaniques qui ne changent pas le long de leurs axes principaux.
Le but de cet exemple est de comparer les résultats en termes de déplacement vertical. La configuration du modèle est illustrée à la figure 5.
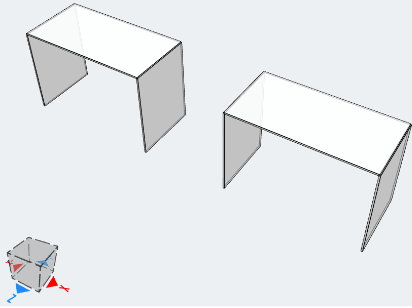 Figure 5. Configuration du modèle. Orthotrope (la gauche), Isotrope (droite)
Figure 5. Configuration du modèle. Orthotrope (la gauche), Isotrope (droite)
Propriétés mécaniques
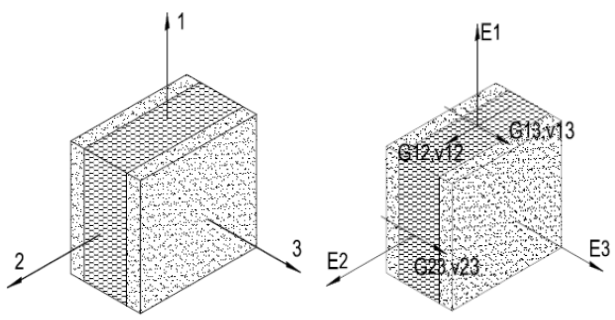
Basé sur différents rapports de tests de laboratoire, les propriétés orthotropes du panneau sont (Torres Villavicencio et al, 2013):
| Propriété | Valeur |
|---|---|
| E1 (MPa) | 5613 |
| E2 (MPa) | 5613 |
| E3 (MPa) | 2807 |
| g12 (MPa) | 2245 |
| g23 (MPa) | 1123 |
| g13 (MPa) | 1123 |
| n12 | 0.2 |
| n23 | 0.25 |
| n13 | 0.25 |
Tableau n°1. Propriétés mécaniques orthotropes du panneau sandwich
Figure n°6. Axes principaux dans l'élément de panneau (Torres Villavicencio et al, 2013).
Les approximations pour le cas isotrope sont indiquées dans le tableau ci-dessous.
| Propriété | Valeur |
|---|---|
| E (MPa) | 5613 |
| g (MPa) | 2245 |
| n | 0.20 |
Tableau n°2. Approximation des propriétés mécaniques isotropes du panneau sandwich
Modélisation dans SkyCiv
Nous décrivons maintenant de manière très concise les étapes nécessaires pour modéliser l'exemple. (Pour plus de détails dans la modélisation des plaques, consulter ce lien Modélisation de plaques SkyCiv). Je n'ai pas essayé SkyCiv, suivre avec Structural 3D, vous n'avez qu'à Inscrivez-vous gratuitement ici.
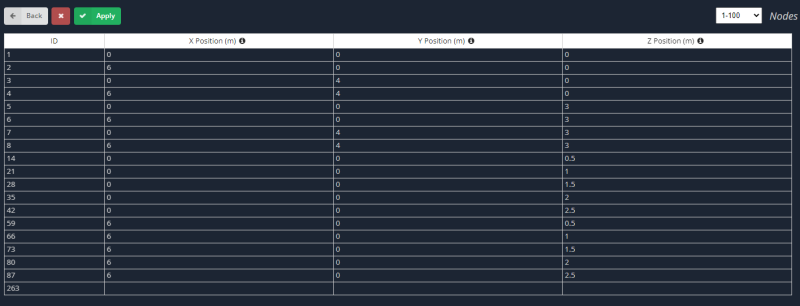
- Nœuds: Pour créer les deux cas, on définit d'abord les nœuds correspondant aux plaques horizontales et verticales.

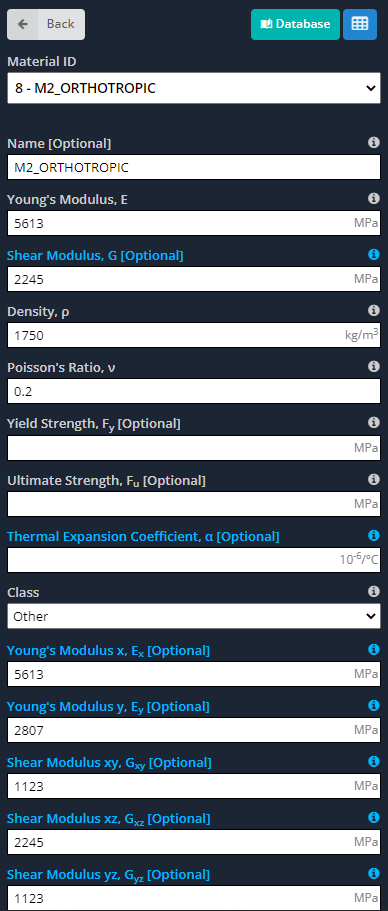
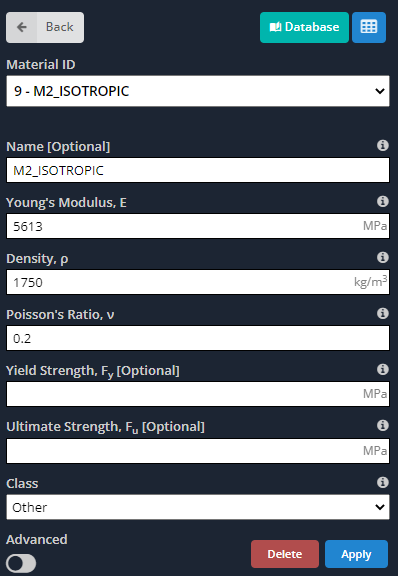
- Matériaux: Comme nous l'avons dit auparavant, les matériaux orthotropes ont des propriétés différentes le long de leurs axes principaux. Les images suivantes indiquent les entrées que nous devons définir pour le modèle.


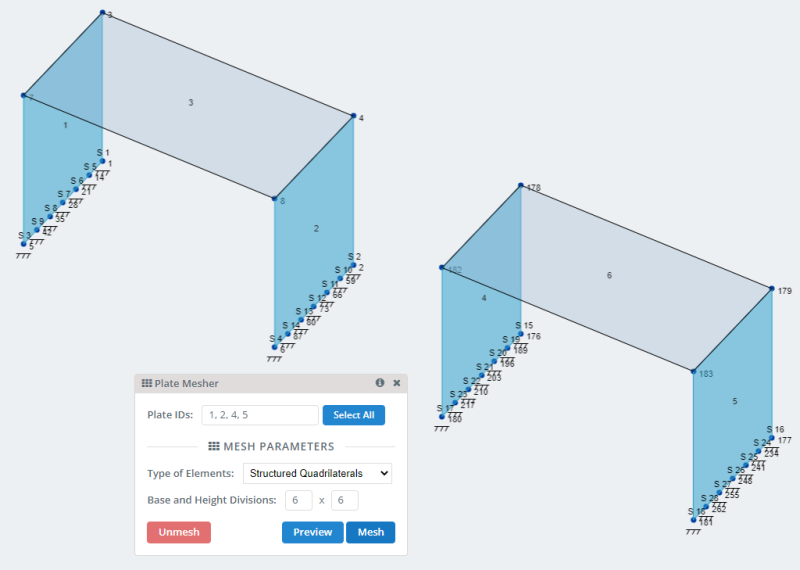
- Plaques: À travers les nœuds du modèle, nous créons les plaques rectangulaires. Deux pour la modélisation verticale des murs et un pour le sol ou la dalle.

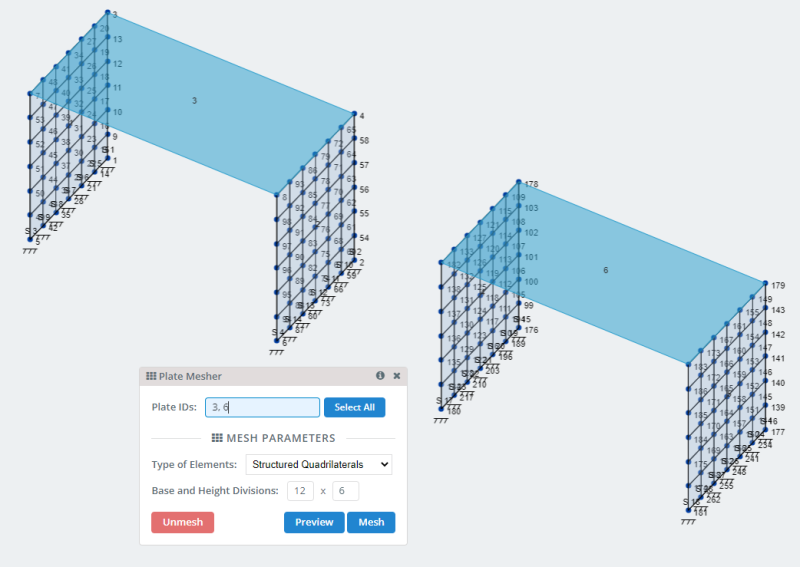
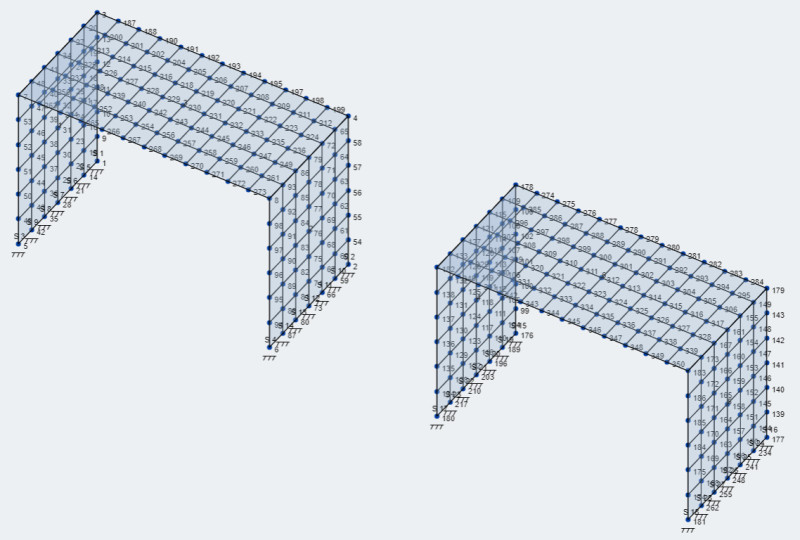
- Plaques de maillage: SkyCiv a de nombreuses options pour mailler les plaques et peut être consulté dans Maillage de votre assiette . Pour notre modèle, utilisons l'option de maillage de quadrilatères structurés.



- Définition du cas de charge de poids propre: Nous ne considérerons cette charge de poids propre que pour capturer le comportement structurel général de la plaque.

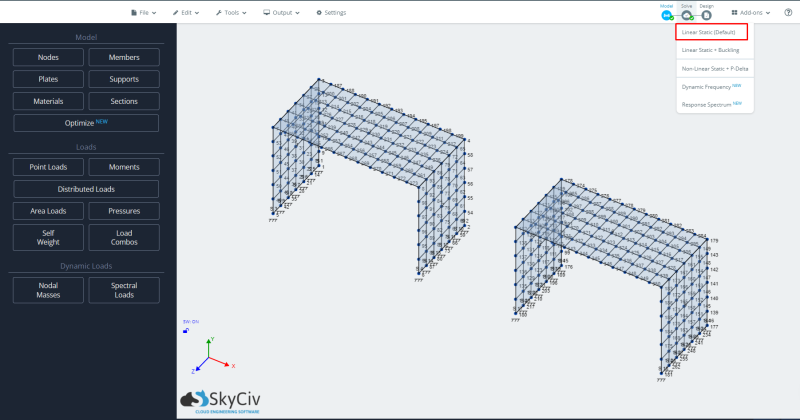
- Analyse en cours: Pour exécuter le modèle, nous sélectionnerons le cas d'analyse statique linéaire.

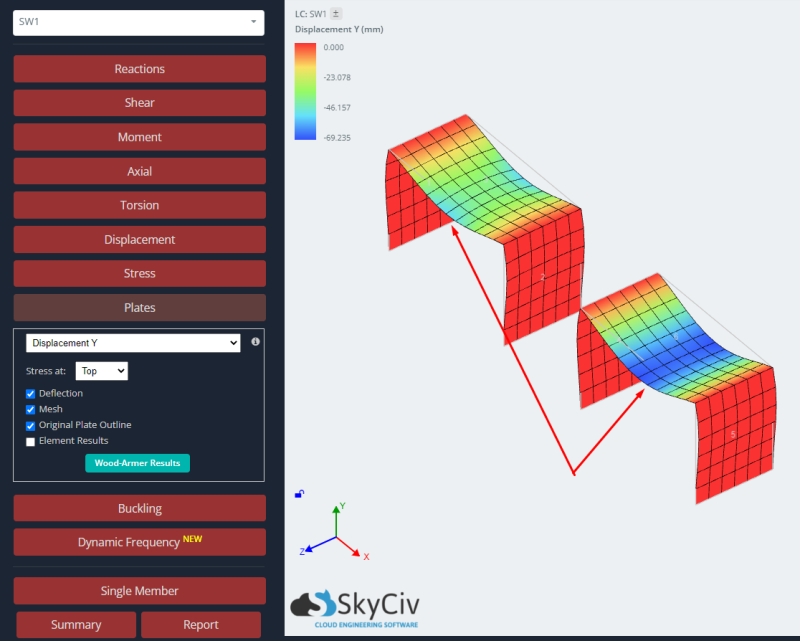
- Résultats: Ensuite, à ce stade, nous étudions la réponse structurelle pour les deux plaques, le cas isotrope et orthotrope. Pour plus de détails dans la lecture des résultats pour l'analyse des plaques, tu peux regarder cet article Résultats de l'analyse des plaques.

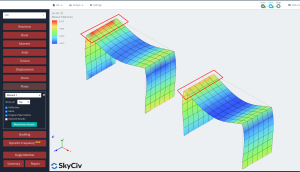
Pour étudier la réponse des deux cas, nous comparons les résultats de déplacement vertical et de moment de flexion. La plaque orthotrope montre des déflexions plus petites et des moments de flexion plus grands que le cas isotrope. Nous pouvons dire que l'utilisation d'une approche orthotrope nous donnera un élément plus rigide et cela aura un impact sur les résultats globaux et locaux dans une analyse linéaire élastique.
Commencez gratuitement
Vérifier SkyCiv Structural 3D gratuitement aujourd'hui pour avoir un avant-goût de notre logiciel!
Références:
- Chandrupatla, Tirupathi R & Belegundu, Ashok (2012). “Introduction aux éléments finis en ingénierie” 4ème édition, Éducation Pearson.
- W. Jiang et al (1997). “Modélisation par éléments finis de plaques orthotropes raidies et non raidies”, Des ordinateurs & Structures Vol.63, N°1, pp. 105-117, Elsevier Science Ltd.
- Torres Villavicencio et al (2013). “travail monographique: Aides à la conception pour les systèmes porteurs EMMEDUE de panneaux en béton armé avec âme en P.E.S. (Système de polystyrène expansé)”. Université nationale d'Ingéniérie.
- Toutes les images logicielles tirées de Logiciel d'analyse 3D structurelle SkyCiv