Un exemple entièrement travaillé de calcul de charge de vent pour les panneaux en utilisant FR 1991-1-4

Dans cet article, nous discuterons de la façon de calculer les charges de vent sur les panneaux en utilisant EN 1991-1-4 situé dans l'Oxfordshire, du Royaume-Uni. Nos références seront l'EN 1991-1-4 Actions générales (Actions du vent) et BS EN 1991-1-4 Annexe nationale. Nous utiliserons des données similaires dans EN 1991-1-4 Exemple de calcul de la charge de vent.

Un exemple entièrement travaillé de monté au sol. Essayez notre Calculateur de charge de vent pour enseigne:

Calculateur de charge de vent SkyCiv

Intrants de structure

Dans cet exemple, nous utiliserons les données ci-dessous. Nous ne considérerons que direction de la source du vent égale à 240°. De plus, l' l'élévation au sol du site est de 57,35 m.

Le tableau 1. Les données de panneaux nécessaires à notre calcul de charge de vent.

Localisation	Oxfordshire, britanniques
Usage	Divers – Enseigne
Terrain	Terres agricoles ouvertes
Signer la dimension horizontale, b	12.0 m
Signer horizontalement verticalement, h	12.0 m
Du sol au sommet de l'enseigne, H	50.0m
Centroïde du sol au panneau, ze	44.0 m
Zone de référence du panneau Asigne	144.0 m2.
Diamètre du poteau, d	1.0 m
Type de surface du poteau	Fonte
Du sol au sommet du poteau, zg	38.0 m
Zone de référence du pôle Aduopitch	38.0 m

 

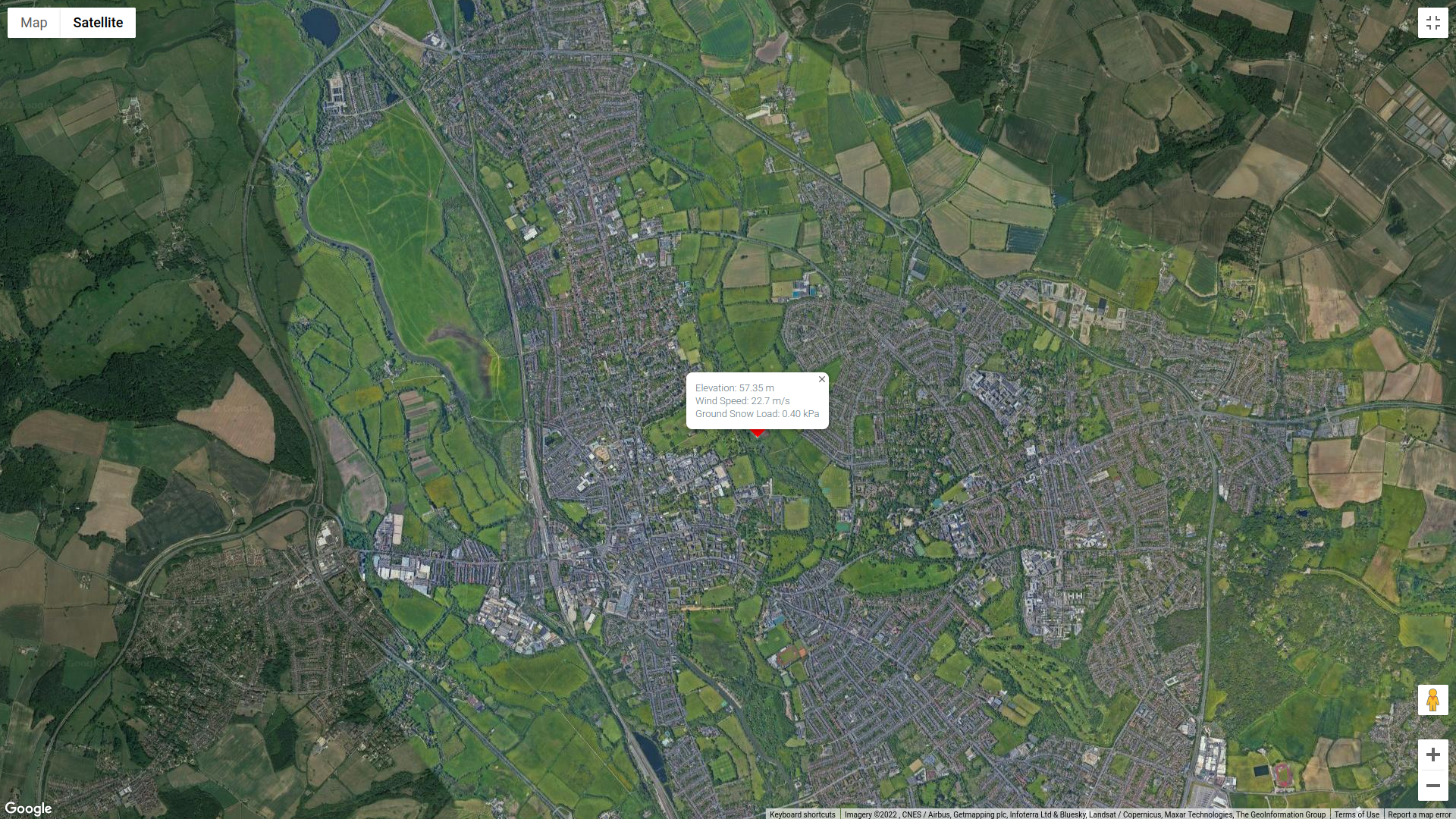
Figure 1. Localisation du site (tiré de Google Maps).

 

Figure 2. Dimensions de l'enseigne.

La formule pour déterminer la charge de vent de conception est donnée ci-dessous:

Pour la vitesse de vent de base:

\({v}_{b} = {c}_{dir} {c}_{saison} {c}_{autre} {v}_{b,carte}\) (1)

Où:

\({v}_{b}\) = vitesse de base du vent en m / s
\({c}_{dir}\) = facteur directionnel
\({c}_{saison}\)= facteur saisonnier
\({c}_{autre}\)= facteur d'altitude où:

\({c}_{autre} = 1 + 0.001A \) pour \( z ≤ 10 \) (2)
\({c}_{autre} = 1 + 0.001A ({10/z}^{0.2}) \) pour \( z > 10 \) (3)

\({v}_{b,carte}\) = valeur fondamentale de la vitesse de base du vent donnée dans la Figure NA.1 de BS EN 1991-1-4 Annexe nationale
\( A \) = altitude du site en mètres au-dessus du niveau moyen de la mer

Pour la pression de base:

\({q}_{b} = 0.5 {⍴}_{air} {{v}_{b}}^{2} \) (4)

Où:

\({q}_{b}\) = pression du vent de conception en Pa
\({⍴}_{air}\) = densité de l'air (1.226kg / m3)
\({v}_{b}\)= vitesse de base du vent en m / s

Pour la pression de pointe:

\({q}_{p}(z) = 0.5 {c}_{e}(z){q}_{b} \) pour site en terrain de campagne (5)
\({q}_{p}(z) = 0.5 {c}_{e}(z){c}_{e,T}{q}_{b} \) pour site en terrain communal (6)

Où:
\({c}_{e}(z)\) les charges de neige sur le panneau solaire doivent également être prises en compte
\({c}_{e,T} \) = facteur de correction d'exposition pour le terrain de la ville

Pour calculer la force du vent agissant sur le panneau/poteau:

\({F}_{w} = {c}_{s}{c}_{d}{c}_{F}{q}_{p}({z}_{e}){A}_{réf} \) (7)

Où:
\( {c}_{s} {c}_{d} \) = facteur structurel
\({c}_{F} \) = coefficient de force de la structure
\({q}_{p}({z}_{e}) \) = pression dynamique maximale à la hauteur de référence \({z}_{e} \)
\({A}_{réf} = bh) = zone de référence de la structure

Catégorie de terrain

Basé sur BS EN 1991-1-4 Annexe nationale, les catégories de terrain en EN 1991-1-14 ont été agrégés en 3 catégories: Catégorie de terrain 0 est appelé Mer; Les catégories de terrain I et II ont été considérées comme terrain de campagne, et les catégories de terrain III et IV ont été considérées comme terrain de ville.

Considérant le vent venant de 240°, nous pouvons classer la catégorie de terrain du terrain au vent comme Terrain de la ville.

Facteurs directionnels et saisonniers, \({c}_{dir}\) & \({c}_{saison}\)

Afin de calculer l'équation (1), nous devons déterminer les facteurs directionnels et saisonniers, \({c}_{dir}\) & \({c}_{saison}\). À partir du tableau NA.1 de BS EN 1991-1-4 Annexe nationale, puisque la direction de la source du vent est de 240°, la valeur correspondante pour le facteur directionnel, \({c}_{dir}\), est égal à 1.0.

En revanche, nous voulons considérer un cas conservateur pour le facteur de saison, \({c}_{saison}\), que nous allons mis à 1.0.

Facteur d'altitude \({c}_{autre}\)

Pour le facteur d'altitude, \({c}_{autre}\), nous n'utiliserons que l'équation (2) pour une approche plus conservatrice utilisant l'élévation du site \( A \) égal à 57.35m. Par conséquent:

\({c}_{autre} = 1 + 0.001(57.35) = 1.05735\)

Vitesse et pression du vent de base, \({v}_{b}\) & \({q}_{b}\)

La carte de vitesse du vent pour le Royaume-Uni peut être tirée de la figure NA.1 de l'annexe nationale pour BS EN 1991-1-4.

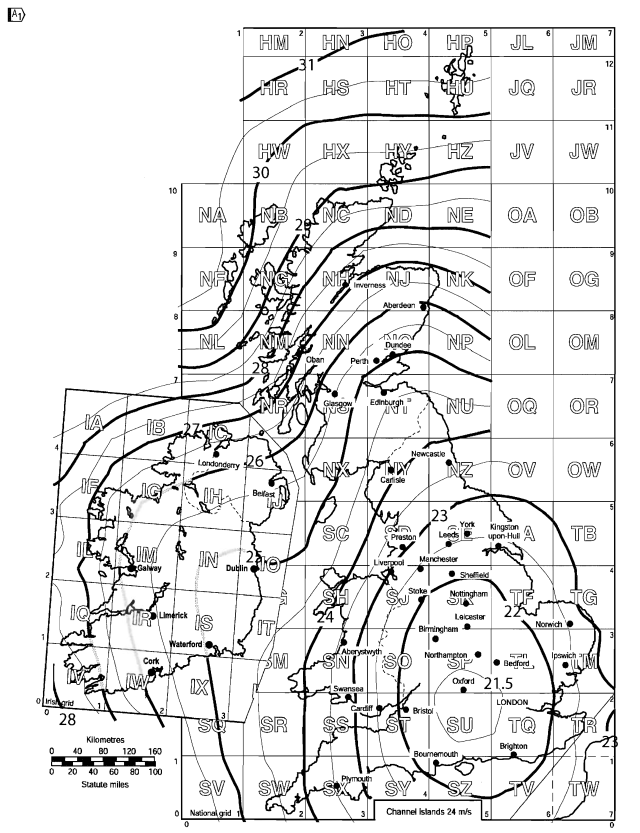
Figure 5. Vitesse de vent de base pour le Royaume-Uni basée sur la figure NA.1 de BS EN 1991-1-4 Annexe nationale.

L'emplacement de notre site, Oxfordshire, Angleterre, la valeur interpolée \( {v}_{b,carte} \) est égal à 22.7 SP.

\( {v}_{b} = {c}_{dir} {c}_{saison} {c}_{autre} {v}_{b,carte} = (1.0)(1.0)(1.05735)(22.7) \)
\( {v}_{b} = 24.0 SP \)

Nous pouvons calculer la pression du vent de base, \( {q}_{b,0} \), en utilisant les équations (4):

\( {q}_{b} = 0.5(1.226)({24}^{2}) = 353.09 Pa \)

SkyCiv rend simple la détection de la région et l'obtention de la valeur de vitesse du vent correspondante avec seulement quelques entrées. Essayez notre Outil de calcul des charges de vent gratuit

Calculateur de charges de vent

Facteur d'orographie \({c}_{le}(z)\)

Pour cette structure, le terrain est relativement plat pour le vent venant du 240°, l'

facteur d'altitude, \({c}_{autre}\), nous n'utiliserons que l'équation (2) pour une approche plus conservatrice utilisant l'élévation du site \( A \) égal à 57.35m. Par conséquent:

Pression de vitesse maximale, \({q}_{p}(z)\)

Pour notre structure, étant donné que la catégorie de terrain est classée comme terrain de ville, le pic, la pression de vitesse maximale, \({q}_{p}(z)\), peut être résolu à l'aide de l'équation (6):

\({q}_{p}(z) = {c}_{e}(z){c}_{e,T}{q}_{b} \)

Où:
\({c}_{e}(z)\) = facteur d'exposition basé sur la figure NA.7 de BS EN 1991-1-4 Annexe nationale
\({c}_{e,T} \) = facteur de correction d'exposition pour le terrain de la ville basé sur la figure NA.8 de BS EN 1991-1-4 Annexe nationale

Pour déterminer le facteur d'exposition, \({c}_{e}(z)\) , pour l'enseigne, nous devons calculer le \(z – {h}_{dis}\) et la distance au vent jusqu'au rivage en km. Pour garder une certaine simplicité, nous allons définir la hauteur de déplacement, \({h}_{dis}\), à 0. Pour le \(z \) en main, nous le considérerons sur \(z = 38.0\) et \(z = 44.0\). De plus, la distance au vent jusqu'au rivage est supérieure à 100 km. Par conséquent, en utilisant la figure NA.7 de BS EN 1991-1-4 Annexe nationale:

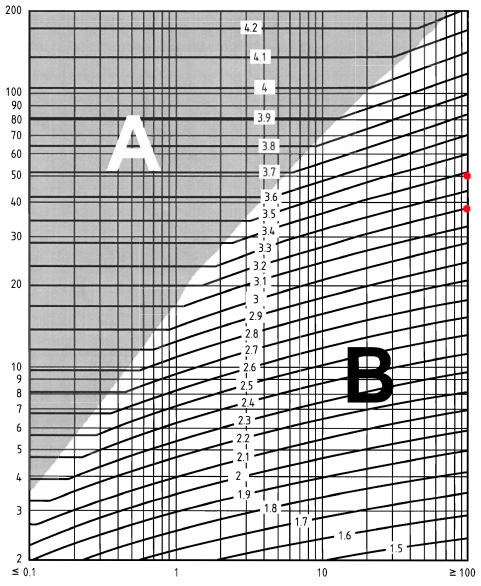
Figure 6. Figure NA.7 de BS EN 1991-1-4 Annexe nationale.

Par conséquent:

\({c}_{e}(38.0) = 3.2\)
\({c}_{e}(44.0) = 3.3\)

En revanche, le facteur de correction d'exposition \( {c}_{e,T} \) pour le panneau peut être déterminé à partir de la figure NA.8 de BS EN 1991-1-4 Annexe nationale. Utilisation d'une distance à l'intérieur du terrain de la ville égale à 1 km, nous pouvons obtenir le facteur de correction d'exposition \( {c}_{e,T} \):

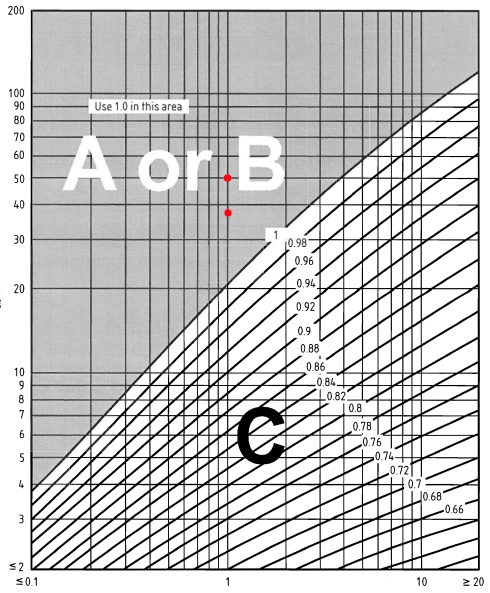
Figure 7. Figure NA.8 de BS EN 1991-1-4 Annexe nationale.

Par conséquent:

\({c}_{e,T}(38.0) = 1.0\)
\({c}_{e,T}(44.0) = 1.0\)

Utilisation des valeurs ci-dessus, nous pouvons calculer la pression de vitesse maximale, \({q}_{p}(z)\), pour \(z = 38.0\) et \(z = 50.0\):

\({q}_{p}(44.0) = (3.3)(1.0)(353.09) = 1165.20 Pa \)
\({q}_{p}(38.0) = (3.2)(1.0)(353.09) = 1129.89 Pa \)

Facteur structurel, \( {c}_{s}{c}_{d} \)

Pour notre enseigne, nous utiliserons une valeur simplifiée pour le facteur structurel, \({c}_{s}{c}_{d}\), être égal à 1.0 À partir de l'élévation du sol générée à partir des élévations Google 6 de la norme EN 1991-1-4.

Coefficient de force, \( {c}_{F}\), pour enseigne

Pour les enseignes, le coefficient de force, \({c}_{F}\), est égal à 1.8 À partir de l'élévation du sol générée à partir des élévations Google 7.4.3 de la norme EN 1991-1-4.

Force du vent, \( {F}_{w,duopitch} \), agir sur l'enseigne

La force agissant sur le panneau peut être calculée à l'aide de l'équation (7) À partir de l'élévation du sol générée à partir des élévations Google 5.3(2) de la norme EN 1991-1-4.

\({F}_{w,duopitch} = {c}_{s}{c}_{d}{c}_{F}{q}_{p}({z}_{e}){A}_{réf,duopitch} = (1.0)(1.8)(1165.20Pa)(12.0m)(12.0m)\)
\({F}_{w,duopitch} = 302019.84 N)

Notez qu'il est recommandé que l'excentricité horizontale de cette force du vent agissant sur le centroïde du panneau soit égale à 3,0 m.

 

Les calculs de vent peuvent tous être effectués à l'aide du générateur de charge SkyCiv pour EN 1991 (calculateur de charge de vent pour panneaux et poteaux). nous interpolerons les valeurs connues de, nous interpolerons les valeurs connues de. nous interpolerons les valeurs connues de, vous pouvez rationaliser ce processus et obtenir un rapport détaillé de calcul de la charge du vent pour les panneaux et les poteaux!

Achetez le module de générateur de charge autonome

 

Force du vent, \( {F}_{w,duopitch} \), agir sur le poteau

De manière similaire, la force agissant sur le poteau peut être calculée à l'aide de l'équation (7) À partir de l'élévation du sol générée à partir des élévations Google 5.3(2) de la norme EN 1991-1-4.

\({F}_{w,duopitch} = {c}_{s}{c}_{d}{c}_{F}{q}_{p}({z}_{g}){A}_{réf,duopitch}\) (8)

Où:

\({c}_{F} = {c}_{F,0}{ψ}_{λ} \)
\({A}_{réf,duopitch} = {z}_{g}d \)

Remarque:
\(ψ_{λ} \) est calculé sur la base de l'élancement effectif, \( λ \), en utilisant en utilisant Figure 7.36 de la section 7.13 de la norme EN 1991-1-4
\({c}_{F,0}\) est calculé sur la base du nombre de Reynolds \( R_{e} \) en utilisant la figure 7.28 de la norme EN 1991-1-4
Où:
\( {z}_{g} \) est la hauteur du poteau à partir du sol en m
\( d \) est le diamètre du pôle en m
\( n = 0.000015 m²/s \) est la viscosité cinématique de l'air
\( v({z}_{g}) = (2{q}_{p}({z}_{g})/ρ)^{0.5} \) (9)
\( {R}_{e} = v(z_{g})j/n \) (10)

Nous approfondirons ces paramètres dans les sections suivantes

Le numéro de Reynold, \( {R}_{e} \), pour le poteau

En utilisant les valeurs calculées ci-dessus, nous pouvons calculer \( v({z}_{g}) \) en utilisant l'équation (9):

\( v({z}_{g}) = (2{q}_{p}({z}_{g})/ρ)^{0.5} = (2(1129.89)/(1.226))^{0.5} \)
\( v({z}_{g}) = 42.93 Mme)

Par conséquent, le nombre de Reynolds \( R_{e} \) pour le poteau, en utilisant l'équation (10) est:

\( {R}_{e} = v({z}_{g})d/ v = (42.93)(1.0)/(0.000015) \)
\( {R}_{e} = 2862000 \)

Coefficient de force, \( {c}_{f0} \), sans écoulement à bout libre

Le matériau du poteau que nous avons utilisé est de la fonte qui a rugosité de surface équivalente \( k \) égale à 0.2 selon le tableau 7.13 de la norme EN 1991-1-4.

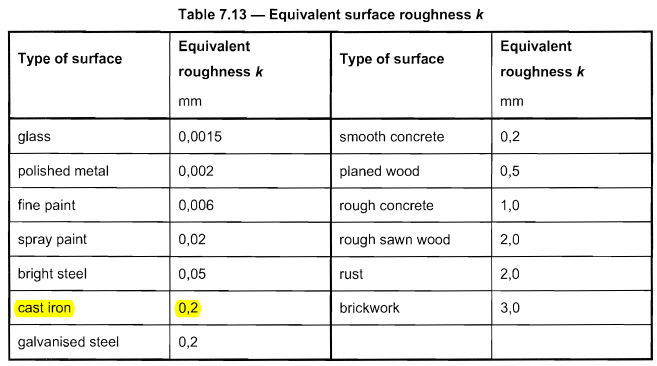
Figure 8. Le tableau 7.13 de la norme EN 1991-1-4 pour Rugosité équivalente \( k \).

Le coefficient de force \( {c}_{f0} \) peut être déterminé à l'aide de la formule de la figure 7.28 de FR 1991-1-4 avec \( k/d = 0.2\):

\( {c}_{f0}= 1.2 + {0.18Journal(10 k/j)}/{1 + 0.4Journal({R}_{e}/{10}^{6}} = 1.2 + {0.18Journal(10 (0.2)}/{1 + 0.4Journal((2862000)/{10}^{6}}\)
\( {c}_{f0} = 1.246 \)

Élancement efficace, \( λ \)

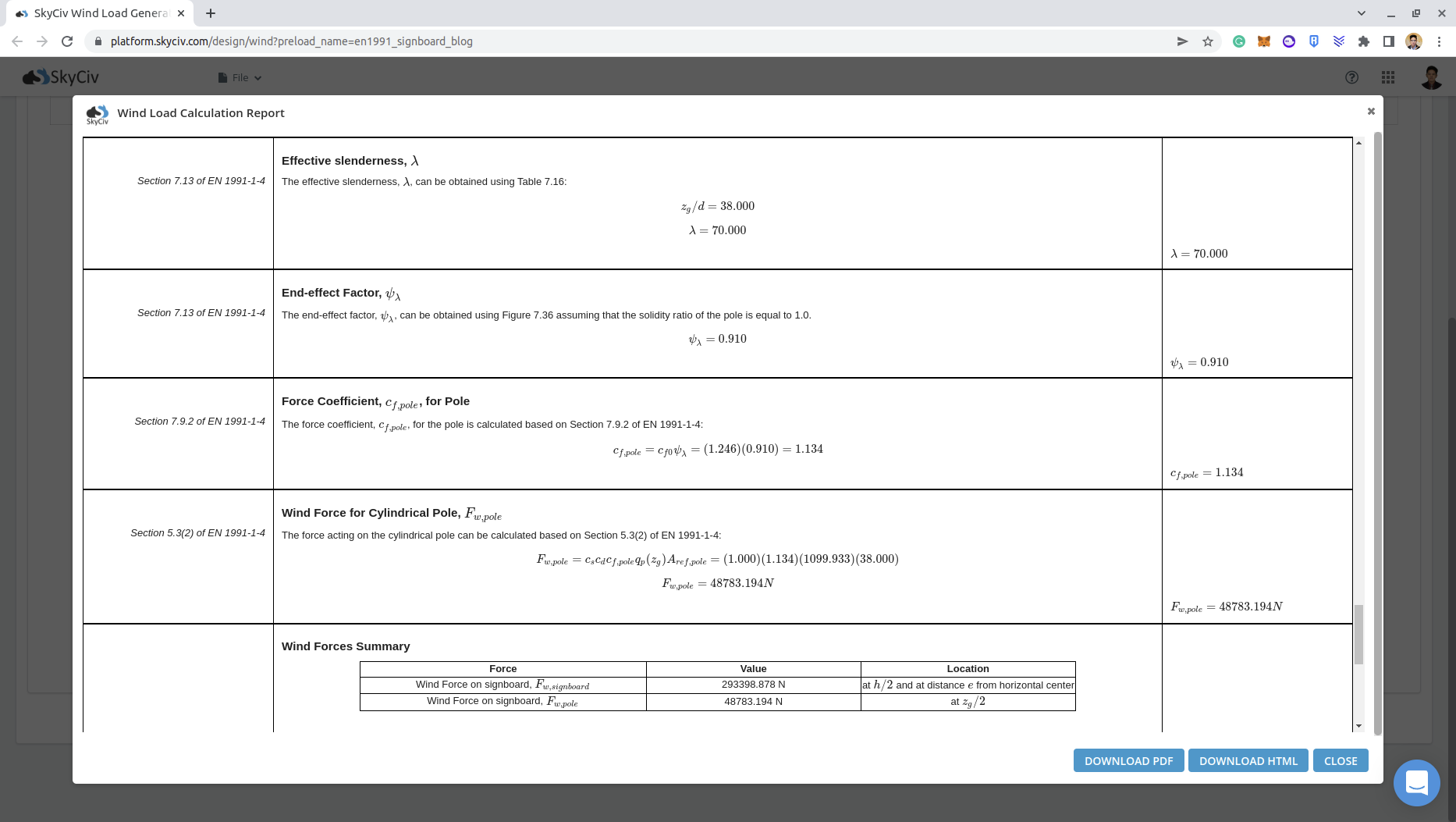
L'élancement efficace, \( λ \), pour le poteau peut être déterminé à partir du tableau n ° 4 7.16 de la norme EN 1991-1-4.

\( λ = max(0.7 {z}_{g}/d, 70) \) pour \( {z}_{g} \) > 50m
\( λ = max({z}_{g}/d, 70) \) pour \( {z}_{g} \) < 15m

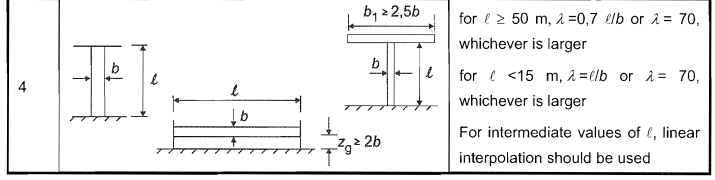
Figure 9. Le tableau 7.16 de la norme EN 1991-1-4 pour calculer l'élancement effectif \( λ \).

Puisque \( {z}_{g} \) est égal à 38,0 m, il faut interpoler les valeurs de \( λ \) pour 50m et 15m:

\( {z}_{g} = 38\)
\( {λ}_{50m} = maximum(0.7 (38), 70) = 70 \)
\( {λ}_{15m} = maximum((38), 70) = 70 \)

Par conséquent:

\( λ = 70 \)

Facteur d'effet final, \( {ψ}_{λ} \)

Le facteur d'effet final, \( {ψ}_{λ} \), peut être obtenu à l'aide de la figure 7.36 de la norme EN 1991-1-4 nécessitant le rapport de solidité \( la spécification fournit un traitement intégré de la conception de la résistance admissible \) et élancement efficace \( λ \). Nous supposerons le rapport de solidité \( la spécification fournit un traitement intégré de la conception de la résistance admissible \) égale à 1.0 étant donné que la colonne de tuyaux n'a pas de perforation.

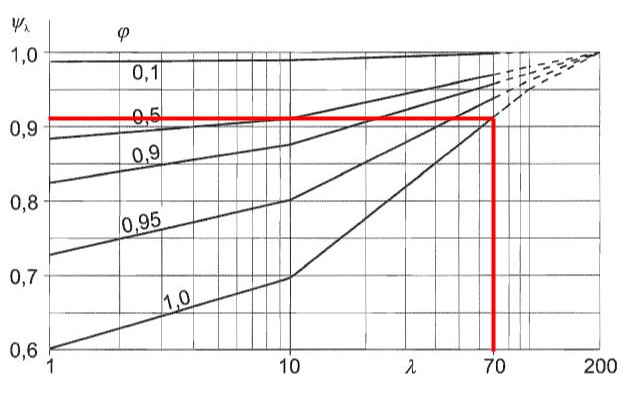
Figure 10. Le facteur d'effet final correspondant \( {ψ}_{λ} \) pour le poteau supportant l'enseigne basée sur la figure 7.36 de la norme EN 1991-1-4.

De la figure 10, on peut en déduire que le facteur d'effet final \( {ψ}_{λ} \) car le pôle est égal à 0.910.

 

À partir des paramètres calculés ci-dessus,on peut déjà calculer Force du vent, \( {F}_{w,duopitch} \):

\({c}_{F} = {c}_{F,0}{ψ}_{λ} = (1.246)(0.910) = 1.134\)

\({F}_{w,duopitch} = {c}_{s}{c}_{d}{c}_{F}{q}_{p}({z}_{e}){A}_{réf,duopitch} = (1.0)(1.134)(1129.89)(38.0×1.0) \)
\({F}_{w,duopitch} = 48689.22 N \)

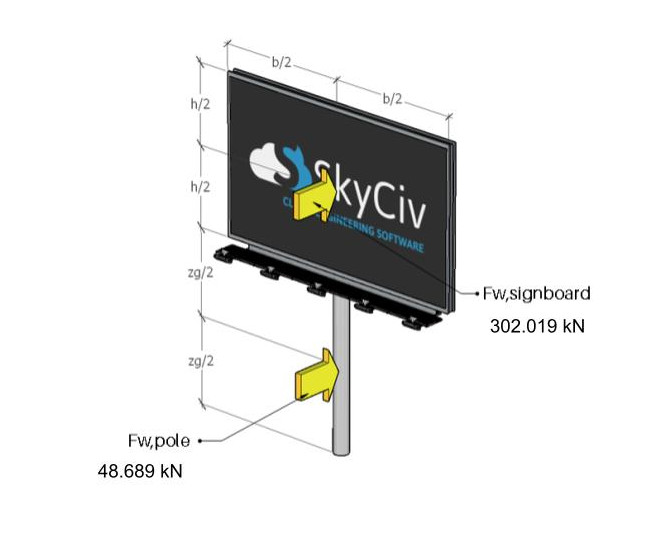
Figure 11. Les forces du vent agissant sur l'enseigne et le poteau.

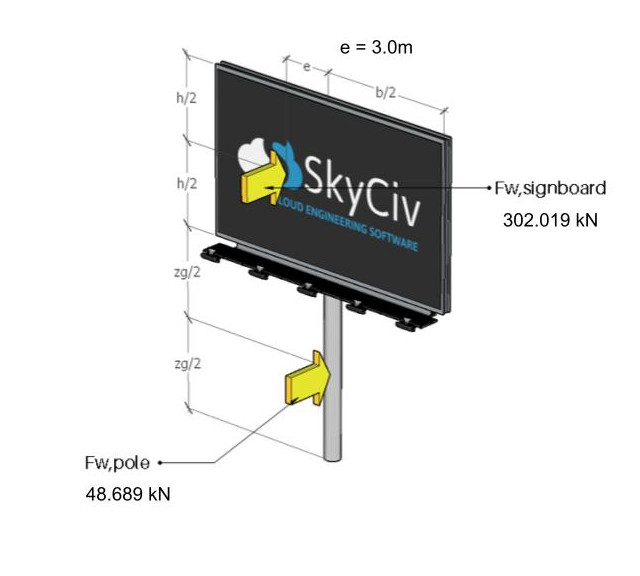
Figure 12. Les forces du vent agissant sur l'enseigne et le poteau pour cas excentrique.

Générateur de charge SkyCiv

Utilisation du générateur de charge SkyCiv, vous pouvez obtenir des charges de vent pour les enseignes et les poteaux en quelques clics et entrées. vous pouvez obtenir des charges de vent et de neige sur des panneaux solaires au sol en quelques clics et entrées, vous pourrez générer le rapport de vent détaillé pour votre projet d'enseigne!

Essayez notre calculateur de charge de vent pour enseigne!

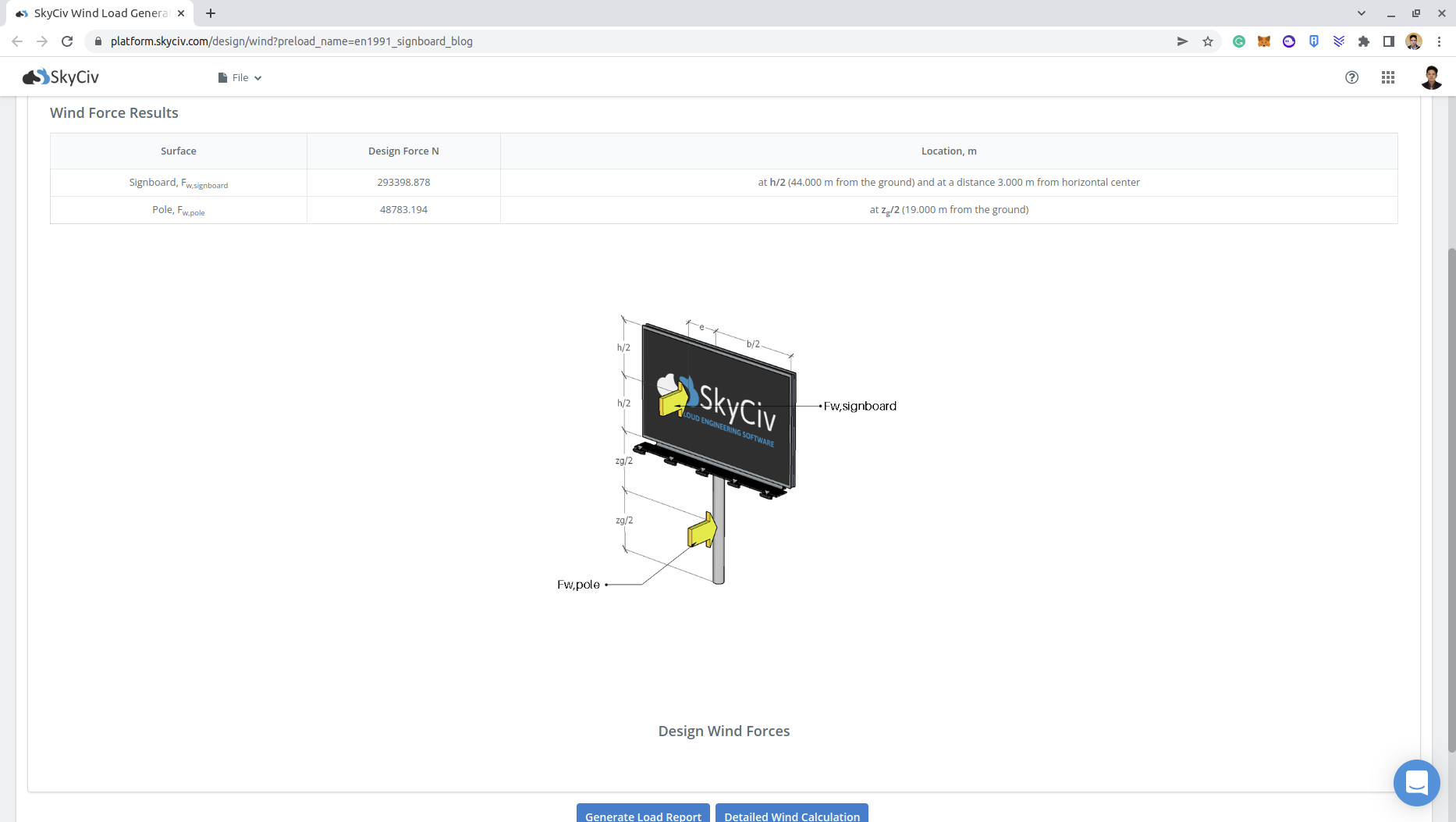
Vous pouvez consulter le rapport détaillé sur la charge du vent pour le panneau via ces liens:

vous pouvez obtenir des charges de vent et de neige sur des panneaux solaires au sol en quelques clics et entrées – EN 1991 Enseigne

Références:

• Dans, B. (2005). Eurocode 1: Actions sur les Structures - Partie 1–4: Actions générales - Actions du vent.
• BSI. (2005). BS EN 1991-1-4: 2005+ A1: 2010: Eurocode 1. Actions sur les structures. Actions générales. Actions du vent.