Un aperçu et un exemple de calcul des charges de neige et comment les appliquer
Les conceptions de toit présentent généralement une multitude d'élévations de toit et offrent rarement une seule hauteur de toit. À cause de ce, il y a des zones de toit plus hautes et plus basses les unes que les autres et sont sujettes à des dérives de neige. La quantité de neige supplémentaire, ou supplément, peut et aura un impact important sur la conception des membres dans ces domaines.
La géométrie du toit et la direction du vent sont les deux facteurs qui conduisent aux dérives de neige. Les deux directions du vent qui provoquent des dérives de neige sont “au vent” et “côté sous le vent”. Les dérives de neige au vent se produisent lorsque le vent souffle la neige d'un toit de basse altitude vers le mur d'un bâtiment adjacent., toit plus haut. Des dérives de neige sous le vent se produisent lorsque le vent souffle la neige d'un toit de plus haute altitude vers un toit inférieur adjacent.. Voir la figure 7-7 selon ASCE 7-10 ci-dessous pour une représentation succincte:

Supposons que notre projet est à Madison, Wisconsin et nous avons déjà calculé notre équilibre, charge de neige sur le toit ici. De notre exemple, notre charge au sol et la charge de neige sur le toit plat se sont avérées 30 psf et 21 psf, respectivement. Les dispositions sur la façon de calculer la surcharge pour la dérive de neige pour les structures se trouvent dans la section 7.8 de l'ASCE 7-10.
Le toit de notre exemple de structure a deux hauteurs de toit différentes. Par conséquent, nous devons calculer la surcharge de neige et l'appliquer à nos membres.. Dans notre cas, nos poutres sont espacées à 10 pieds.
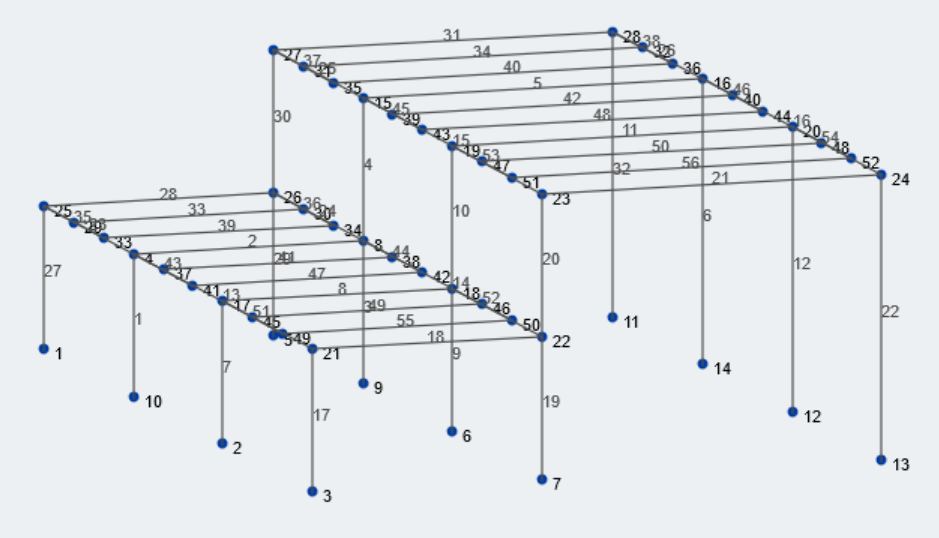
Figure 1: Vue isométrique de notre exemple de structure
Commençons par rassembler les informations géométriques pertinentes sur notre structure. La taille de la baie inférieure et supérieure est 25 pieds et 37 pieds, respectivement. Les élévations de toit inférieures et supérieures sont 15 pieds et 30 pieds du sol, respectivement. La plupart des valeurs géométriques peuvent être associées à des variables. Jetons un coup d'œil à toutes les variables pertinentes pour ce calcul.
\({p}_{g}\) = charge de neige au sol
\({l}_{u}\) = longueur du toit supérieur
\({l}_{l}\) = longueur du toit inférieur
\({h}_{d}\) = hauteur de la dérive de neige
\({w}\) = largeur de la dérive de neige
\({h}_{b}\) = hauteur de la charge de neige équilibrée
\({h}_{c}\) = hauteur libre du haut de la charge de neige équilibrée au point le plus proche du toit adjacent
\({h}_{r}\) = différence de hauteur entre les toits
\({p}_{s}\) = charge de neige de calcul du chapitre 7
\({c}\) = densité de la neige
\({p}_{d}\) = charge de dérive de neige
Jetez un œil à la figure 7-8 selon ASCE 7-10 pour une représentation de plusieurs de ces termes et ce qu'ils représentent visuellement:
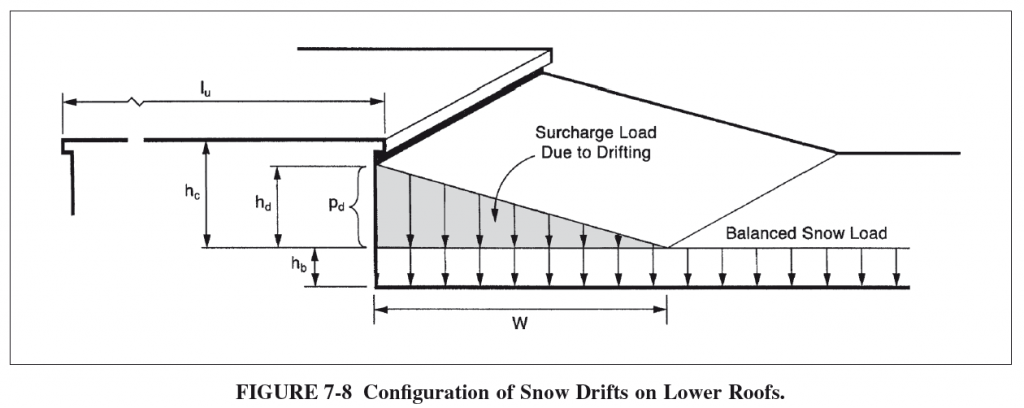
Recherche de la charge supplémentaire de dérive de neige
Maintenant que nous avons identifié quelles sont les variables, les configurations de chargement de neige, et les contraintes géométriques de notre structure, calculons la dérive de la neige.
Première, trouver si le chargement de la dérive de neige est nécessaire, pour ASCE 7.7-1:
Si \({h}_{c}/{h}_{b} < 0.2\), alors l'application de la dérive de neige n'est pas nécessaire.
\({h}_{b} = {p}_{s}/{c}\), où:
\({c} = 0.13{p}_{g} + 14 ≤ 30 pcf\)
\({c} = 0.13*(30) + 14 = 17.9 pcf ≤ 30 pcf \)
\({h}_{b} = {21 psf}/{17.9 pcf } = 1.17 [object Window])
\({h}_{c} = {h}_{r}-{h}_{b}\)
\({h}_{c} = 15 pi – 1.17 ft = 13.8 [object Window])
\({h}_{c}/{h}_{b} = 13.8 pi / 1,17 pi = 11.8 > 0.2\) et donc, le chargement de la dérive de neige est nécessaire.
Seconde, trouver la hauteur de dérive maximale entre les directions au vent et sous le vent:
La hauteur de la dérive pour les deux directions du vent peut être trouvée en utilisant l'équation de la figure 7-9 de l'ASCE 7-10, indiquée ci-dessous:
\({h}_{d} = 3/4*(0.43({l}_{l})^{1/3}({p_g}+10)^{1/4}-1.5)\) pour la dérive au vent
\({h}_{d} = 0.43({l}_{u})^{1/3}({p_g}+10)^{1/4}-1.5\) pour dérive sous le vent
Hauteur de la dérive au vent:
\({h}_{d} = 3/4 *(0.43(25 pi)^{1/3}(30 psf + 10)^{1/4}-1.5)\)
\({h}_{d} = 1.25 [object Window])
Hauteur de la dérive sous le vent:
\({h}_{d} = 0.43(37 pi)^{1/3}(30 psf + 10)^{1/4}-1.5\)
\({h}_{d} = 2.1 [object Window])
La hauteur de dérive maximale entre la hauteur de dérive au vent et sous le vent sera utilisée pour la conception, donc:
\({h}_{d} = 2.1 [object Window])
Prochain, trouver la largeur du supplément de dérive de neige:
La largeur de la charge de neige, \({w}\), dépend de \({h}_{c}\) et \({h}_{d}\)
Par section 7.7.1,
Si \({h}_{d} ≤ {h}_{c}\), ensuite \({w} = 4{h}_{d}\)
Si \({h}_{d} > {h}_{c}\), ensuite \({w} = 4{h}_{d}^ 2 /{h}_{c}) et par la suite \({h}_{d} = {h}_{c}\)
Dans notre cas, \({h}_{c} = 13.8 [object Window]) et \({h}_{d} = 2.1 [object Window]), et donc:
\({h}_{d} ≤ {h}_{c}\), et
\({w} = 4*(2.1 pi)\)
\({w} = 8.4 [object Window])
Remarque, pour ASCE 7-10 l' la largeur de la dérive de neige ne doit jamais dépasser \(8{h}_{c}\)
Durer, calculer la charge de surcharge pour la dérive de neige:
Pour trouver la charge de surcharge maximale, multipliez la hauteur de la dérive par la densité de la neige:
\({p}_{d} = {h}_{d}{c}\)
Dans notre cas,
\({p}_{d} = (2.1 pi)*(17.9 pcf )\)
\({p}_{d} = 37.6 [object Window])
La charge de surcharge maximale de la dérive de neige est ensuite superposée à la charge de neige équilibrée:
\({p}_{max} = {p}_{d}+{p}_{s}\)
\({p}_{max} = 58.6 [object Window])
Application des charges supplémentaires de dérive de neige
Regardons le cadre central de notre structure. La zone distribuée des poutres dans ce plan est 10 ft à cause de la constante 10 espacement des poutres en pieds. Figure 2 ci-dessous illustre la charge de neige équilibrée de 21 psf appliqué sur le toit de notre structure. Remarque, toutes les valeurs ne sont pas pondérées, charges de service.
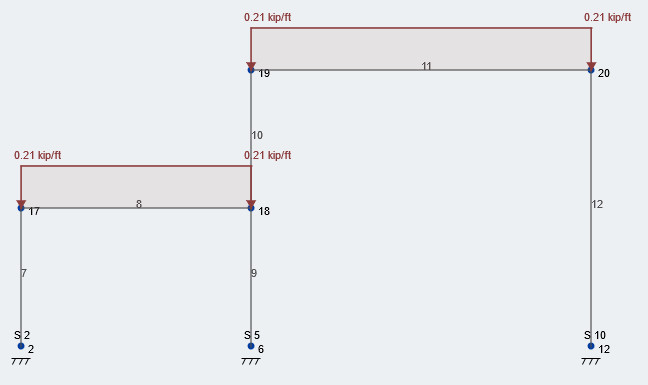
Figure 2: Condition de chargement typique d'une charge de neige équilibrée
Maintenant, prenons la charge de surcharge de la dérive de neige et superposons-la à notre structure. Figure 3 représente la charge de dérive supplémentaire à l'emplacement correct. Comme vous pouvez le voir, notre charge totale de neige est 58.6 psf – arrondi à 59 psf – situé à la face du mur puis décroît linéairement sur la 8.4 largeur de dérive en pieds pour revenir à la charge de neige constante et équilibrée. Cette condition de chargement suit toute la longueur du mur, dans notre cours, la longueur de la structure.
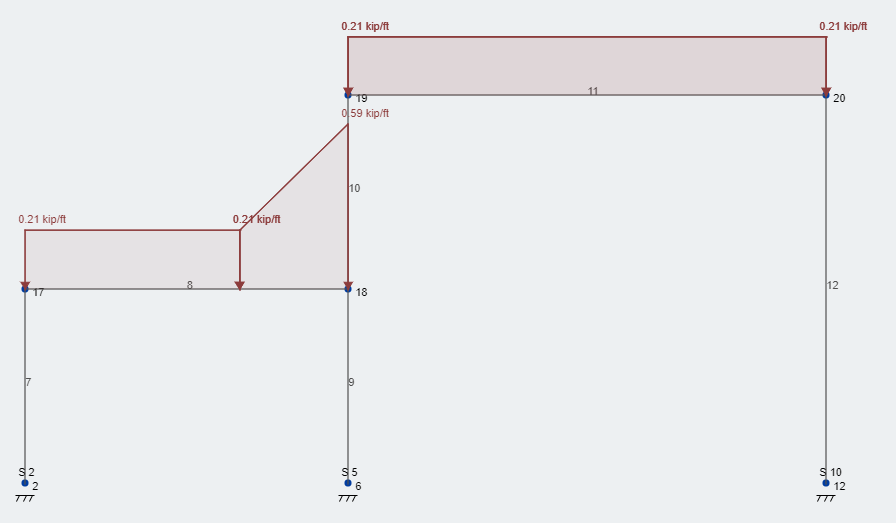
Figure 3: Conditions de chargement typiques des charges de conception de niveau de service
À ce stade, les charges de neige sont prêtes pour l'analyse en conjonction avec d'autres cas de charge et combinaisons de charges basées sur l'ASCE 7-10 et autres codes du bâtiment pertinents. Assurez-vous de lire le chapitre 7 de l'ASCE 7-10 pour plus d'informations sur les dispositions successives pour le chargement partiel de neige et le chargement de neige déséquilibré, car ces conditions n'ont pas été évaluées ici.
Références:
- Charges minimales de conception pour les bâtiments et autres structures. (2013). ASCE / SEI 7-10. Société américaine des ingénieurs civils.


