Dans cet article, nous développerons un exemple de conception de dalle en utilisant la dernière version de l'ACI-318-19: “Exigences du Code du Bâtiment pour le Béton Armé,” consistant en la modélisation dans SkyCiv d'un bâtiment de faible hauteur en béton armé axé sur la comparaison des résultats du logiciel et des calculs manuels par une méthode acceptée par l'ACI: “La méthode de conception directe pour les dalles.” Cette procédure consiste à répartir en différentes bandes le long des directions principales et des cadres du bâtiment le moment total par des facteurs pratiques pour déterminer la quantité de ferraillage et l'emplacement dans la dalle..

Nous espérons que vous avez lu l'article précédent, Conception de plaque en S3D, pour vous initier à la modélisation et à la conception de plaques à l'aide de SkyCiv. Une autre information utile que nous vous suggérons de prendre en compte se trouve dans Comment modéliser des plaques? Une fois que vous avez terminé de lire les deux documents, n'hésitez pas à plonger dans l'exemple de comparaison de dalles complet suivant!

Disposition générale du bâtiment

Les images suivantes montrent une vue isométrique et les dimensions en plan de l'exemple à calculer. Le bâtiment a deux dalles plates surélevées sans poutres entre les supports de colonne.

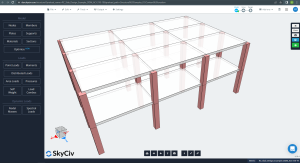
Figure 1. Vue isométrique de l'exemple de bâtiment

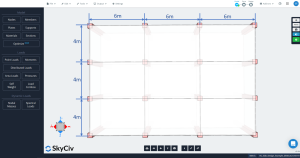
Figure 2. Dimensions du plan de dalle

Méthode de conception directe pour les dalles bidirectionnelles (DDM)

Limites

ACI 318 permet d'utiliser le DDM pour concevoir des dalles en béton armé pour les charges de gravité, qui rassemblent quelques prérequis selon la géométrie, relations de charge, symétrie, etc. Nous pouvons résumer ces limitations dans la liste suivante (Notes de l'APC):

• “Il doit y avoir au moins trois portées continues dans chaque direction.”: Figure 2 montre trois travées dans chaque direction principale, longitudinal et transversal. D'accord!
• “Les panneaux de dalle doivent être rectangulaires avec un rapport de portée plus longue à plus courte (ligne médiane à ligne médiane des supports) pas supérieur à 2.”: Selon chiffre 2, le rapport est égal à \({\frac{l_1}{4}= frac{6m}{4m}=1,5 < 2}\). D'accord!
• “Portées successives (ligne médiane à ligne médiane des supports) dans chaque direction ne doit pas différer de plus de 1/3 de la durée la plus longue”. Les longueurs de portée sont les mêmes dans chaque direction, 6m en longitudinal et 4m en transversal. D'accord!
• “Les colonnes ne doivent pas être décalées de plus de 10% de la travée (dans le sens du décalage) de l'un ou l'autre axe entre les axes des colonnes successives”. L'exemple de bâtiment n'a pas de décalages dans les colonnes. D'accord!
• “Les charges doivent être uniformément réparties, avec la surcharge non pondérée ou de service non supérieure à deux fois la charge permanente non pondérée ou de service (L/D ≤ 2)”. Prendre les valeurs de chaque charge de gravité, le rapport est défini comme \({\frac{L}{D}= frac{2}{7.8}=0,256 < 2}\). D'accord!.
• “Pour les dalles soutenues par des poutres bidirectionnelles, la rigidité relative des poutres dans deux directions perpendiculaires doit satisfaire aux exigences minimales et maximales indiquées dans le code.” Déjà satisfait; il n'y a pas de poutres dans les dalles. D'accord!
• “La redistribution des moments négatifs par code n'est pas autorisée.” En raison de la simplicité de l'exemple, il ne sera pas nécessaire de redistribuer les moments négatifs dans les dalles. D'accord!.

Définition des bandes longitudinales et transversales

La dalle dans DDM doit être divisée en deux bandes principales pour l'analyse et la conception d'une grille de lignes particulière: colonne et bandes médianes. La largeur des bandes de colonnes est la moindre de \({\frac {l_1}{4}}\) et \({\frac{l_2}{4}}\), où \({l_1}\) est la longueur de la portée le long de la grille de lignes et \({l_2}\) est la longueur transversale perpendiculaire.

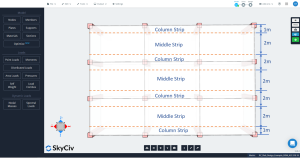
Figure 3. Colonne longitudinale et bandes médianes.

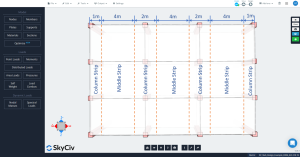
Figure 4. Colonne transversale et bandes médianes.

Épaisseur minimale

ACI-318 suggère d'utiliser l'équation: \({t_{min}}= {\frac{l_n}{30}}={\frac{6m-0.50m}{30}}=0.1833m = 0.20m)

Vérification préliminaire de la résistance au cisaillement

Avant de calculer l'armature d'armature en acier, il est recommandé de vérifier la résistance au cisaillement de la dalle, l'un pour le cisaillement direct dans l'assemblage et l'autre pour la résistance au poinçonnement sur le poteau dalle d'assemblage.

Pour calculer la demande de cisaillement, nous utilisons les charges de gravité suivantes:

• Dalle autoportée: \({SW={\gamma_c}\fois {t_{dalle}}={24 {\frac{kN}{m^3}}}\fois {0.20m}=4,8{\frac{kN}{m^2}} }\)
• Charge morte additionnelle: \({ET={3 {\frac{kN}{m^2}}}}\)
• Charge permanente totale (SW+SD): \({D = {7.8 {\frac{kN}{m^2}}}}\)
• Charge vive (Occupation résidentielle) : \({L={2 {\frac{kN}{m^2}}}}\)
• Charge de résistance pondérée (1.2J+1.6L): \({q_{u}={12.56 {\frac{kN}{m^2}}}}\)

Le premier contrôle de cisaillement est le “cisaillement du faisceau” taper, où l'image suivante indique la zone à considérer pour obtenir le cisaillement total. Nous inspectons chaque direction, en prenant la zone la plus étendue.

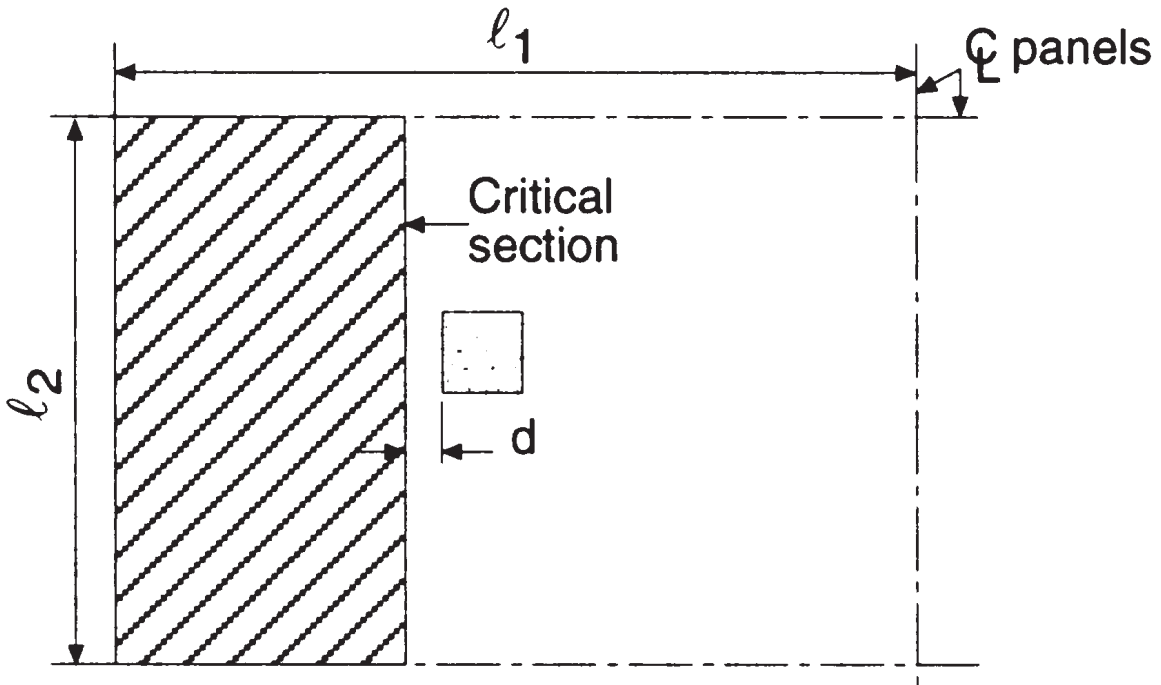
Figure 5. Cisaillement de poutre à l'intérieur du poteau (Nadim Hassoun et Akthem AI-Manaseer, “Théorie et conception du béton structurel”)

Où:

• Portée longitudinale dans le sens longitudinal, \({l_1 = 6.0m }\)
• Portée longitudinale dans le sens transversal, \({l_2 = 4.0m}\)
• Superficie totale des affluents, cisaillement dans le sens longitudinal \({A_t = l_2 fois (\frac{l_1}{2}-\frac{c_1}{2}-d) = 4,0 mfois (\frac{6.0m}{2}-\frac{0.50m}{2}-0.17m) = 10.32 m^2}\) (choisi)
• Superficie totale des affluents, cisaillement dans le sens transversal, \({A_t = l_1 fois (\frac{l_2}{2}-\frac{c_2}{2}-d) = 6,0 mfois (\frac{4.0m}{2}-\frac{0.50m}{2}-0.17m) = 9.48 m^2}\)
• Dimension des colonnes carrées, \({c_1 = c_2 = 0,50m}\)
• Distance d, \({ré = h_{dalle} – couverture = 0.20m – 0.03m = 0,17 m }\)

Par conséquent, le cisaillement maximal de la poutre dans le poteau intérieur est

\({V_u =q_ufois A_t =12,56 {\frac{kN}{m^2}}\fois 10.32 m^2 = 129.62 kN }\)

Cela va être comparé à la résistance au cisaillement, \({\phi_sV_c}\)

• Résistance du béton, \({f'_c = 25 MPa}\)
• Rendement de la résistance de l'acier des barres d'armature, \({f_y = 420 MPa}\)
• \({\phi_s = 0.75}\)
• \({\phi_sV_c = 0,17phi_s lambda sqrt(f'_c) b_w d; b_w=l_2}\)

\({\phi_sV_c = 0,17fois 0,75fois 1fois sqrt(25 MPa) \fois 4000 mmfois 170 millimètre = 433.50 kN }\)

Nous pouvons voir que la résistance au cisaillement est supérieure à la demande de cisaillement: \({\phi_sV_c = 433.50 kN > V_u = 129.62 kN }\) D'accord!.

D'après les images suivantes, nous devons calculer la résistance au poinçonnement et la force à laquelle le béton doit résister dans la liaison dalle-poteau intérieure. L'intention du code lors de la vérification du poinçonnement est de maintenir de faibles valeurs de contrainte de cisaillement.

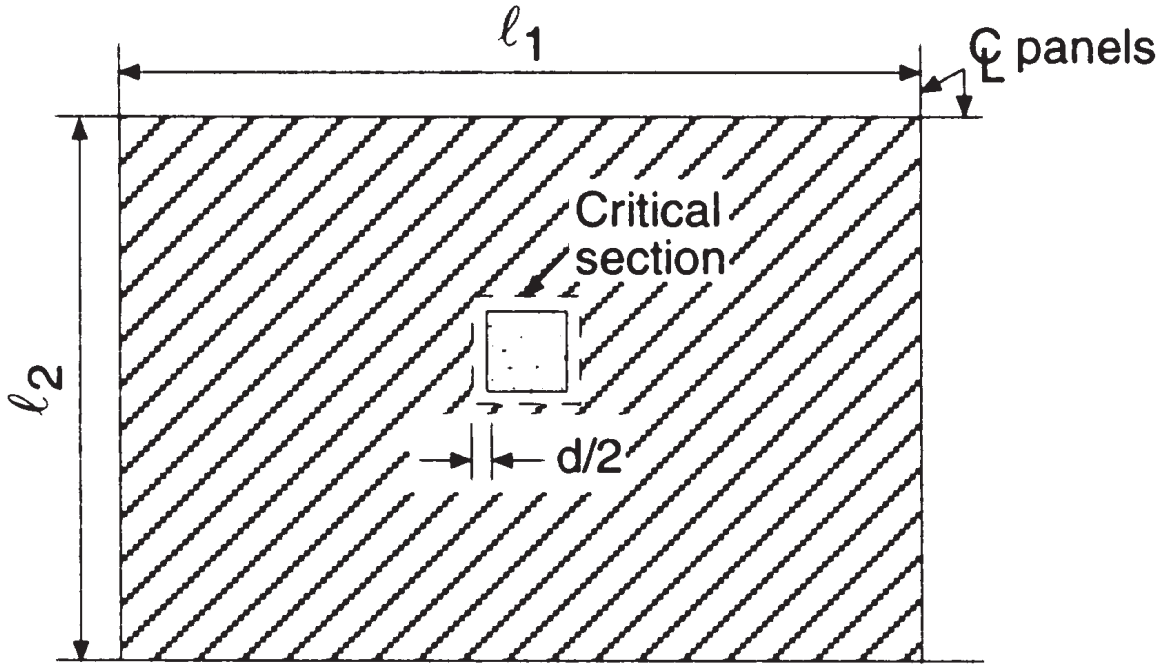
Figure 6. Cisaillement bidirectionnel au niveau du poteau intérieur (Nadim Hassoun et Akthem AI-Manaseer, “Théorie et conception du béton structurel”)

• Superficie totale des affluents, poinçonnage, \({A_t = l_1 fois l_2 – (c_1+d)^2 = 6,0 m fois 4,0 m – (0.50m+0.17m)À partir de l'élévation du sol générée à partir des élévations Google 23.55 m^2}\) (même zone pour les deux directions principales)

La force de cisaillement totale à résister est

\({V_u =q_ufois A_t =12,56 {\frac{kN}{m^2}}\fois 23.55 m^2 = 295.79 kN }\)

Pour obtenir la capacité de poinçonnement dans une dalle bidirectionnelle, nous utiliserons la méthode empirique établie par le code ACI-318, qui considère la contrainte de cisaillement maximale disponible dans le périmètre effectif à la section critique. L'expression la plus conservatrice pour la colonne intérieure est

• Capacité de poinçonnement, \({\phi_sV_c = 0,33phi_s lambda sqrt(f'_c) b_0 j; b_0=4fois (c_1+d)}\)

Par conséquent, on a la résistance au cisaillement de

\({\phi_sV_c = 0,33fois 0.75 \fois 1 \sqrt(25 MPa) \fois (4\fois (500 millimètres+170 millimètres)\fois 170mm) = 563.81 kN }\)

Nous pouvons voir que la résistance au cisaillement est supérieure à la demande de cisaillement: \({\phi_sV_c = 563.81 kN > V_u = 295.75 kN }\) D'accord!.

Nous avons vérifié les exigences de cisaillement unidirectionnel et bidirectionnel à la connexion de la colonne intérieure. En raison du fait que les deux demandes sont inférieures à leurs capacités ou résistances respectives, nous allons maintenant passer au calcul du ferraillage principal pour la flexion de la dalle.

Si vous êtes nouveau chez SkyCiv, Inscrivez-vous et testez le logiciel vous-même!

Inscrivez-vous à SkyCiv!

Moment statique pondéré total par travée.

Le moment maximal qui peut être développé dans une poutre à double extrémité fixe est un moment isostatique égal à \({M = frac{w fois {l_1}^ 2}{8}}\) (Voir figure 6).

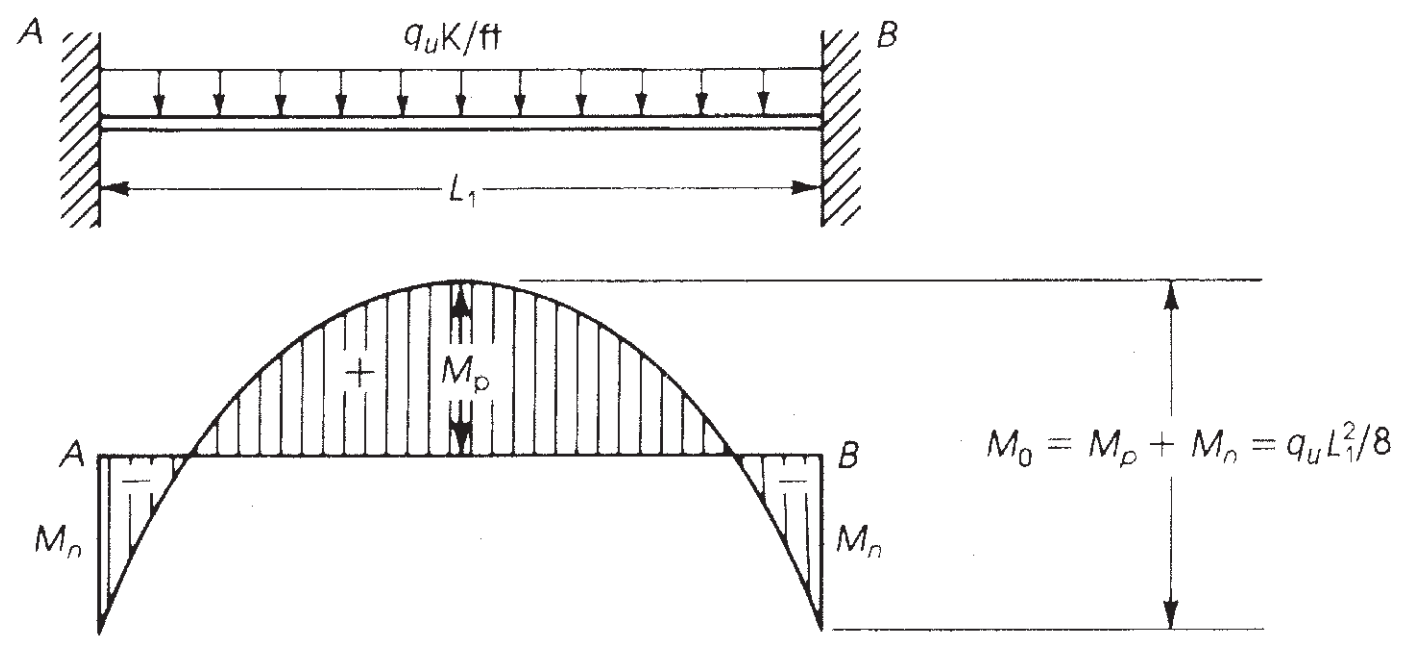
Figure 7. Moment fléchissant dans une poutre à extrémité fixe. (Nadim Hassoun et Akthem AI-Manaseer, “Théorie et conception du béton structurel”)

L'ACI-18 reprend ce principe et, pour la méthode de conception directe (DDM), établit le moment statique maximum à considérer par travée \({M_0}\)

Direction longitudinale:

• \({M_0 = frac {q_ufois l_2fois {l_{n,1}}^ 2}{8}}\)
• \({M_0 = frac {12.56 {\frac{kN}{m^2}}\fois 4.0mfois (6m-0.50m)^ 2}{8}=189,97 kN-m}\)

Direction transversale:

• \({M_0 = frac {q_ufois l_1fois {l_{n,2}}^ 2}{8}}\)
• \({M_0 = frac {12.56 {\frac{kN}{m^2}}\fois 6.0mfois (4m-0.50m)^ 2}{8}=115,40 kN-m}\)

L'étape suivante consiste à attribuer ce moment total en tenant compte du type de panneau, intérieur ou extérieur. (Voir figure 7). Après ça, car les travées sont continues, il faut aussi diviser le moment en positif et négatif. Ce dernier est montré en images 8 et 9.

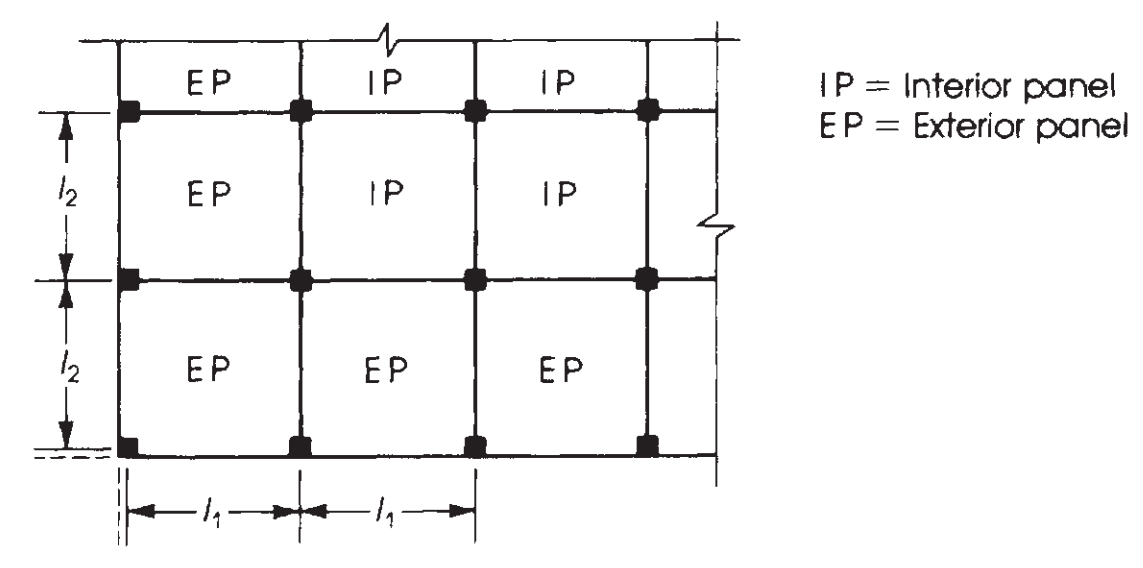
Figure 8. Définition des panneaux selon leur position relative dans un plan de dalle. (Nadim Hassoun et Akthem AI-Manaseer, “Théorie et conception du béton structurel”)

 

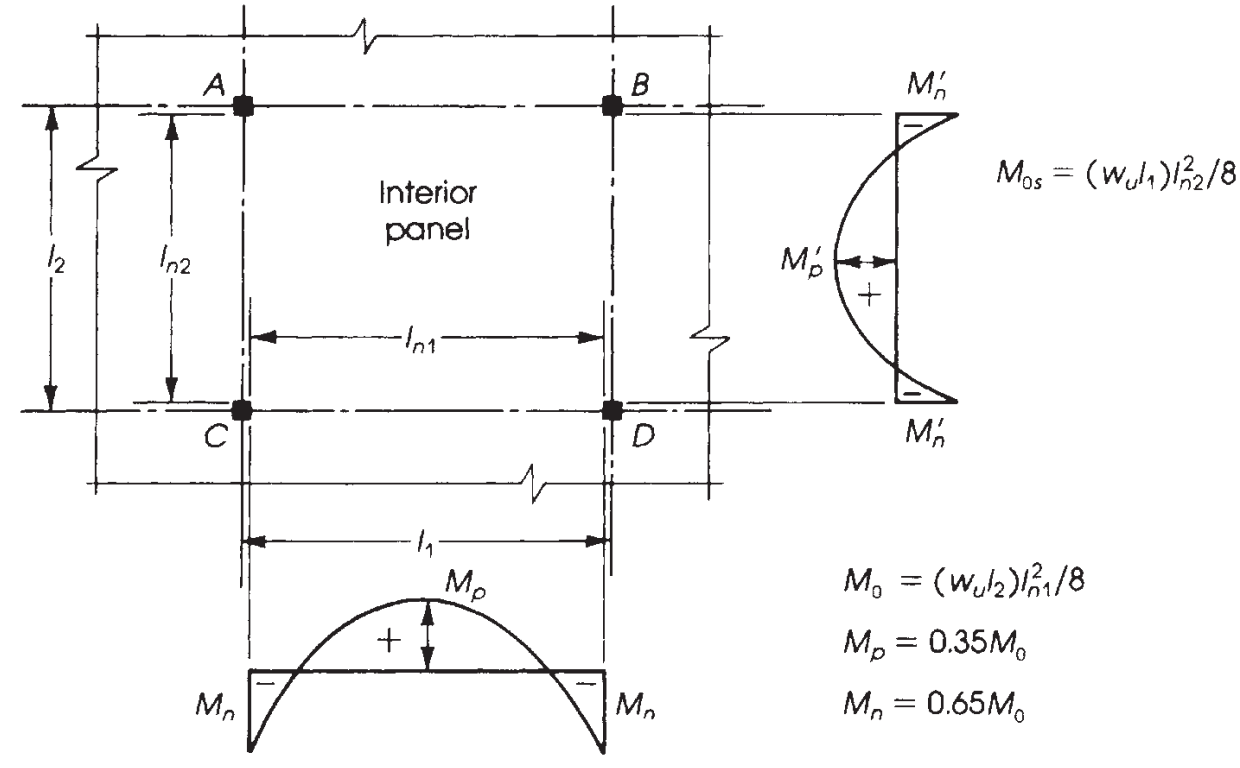
Figure 9. Répartition des moments dans un panneau intérieur. (Nadim Hassoun et Akthem AI-Manaseer, “Théorie et conception du béton structurel”)

 

Il est crucial de connaître la répartition correcte des moments en fonction de la dalle que nous concevons. Dans cet exemple, nous avons le dernier cas dans l'image suivante (figure 9), “Pas de poutres,” appliqué sur une dalle plate ou une dalle pleine sans aucune poutre, ni sur le bord ni entre les supports.

La principale différence dans les cinq cas présentés dans la figure 9 est les fractions de moment à affecter aux panneaux extérieurs, dans lequel la retenue relative à la fin modifie les valeurs à calculer.

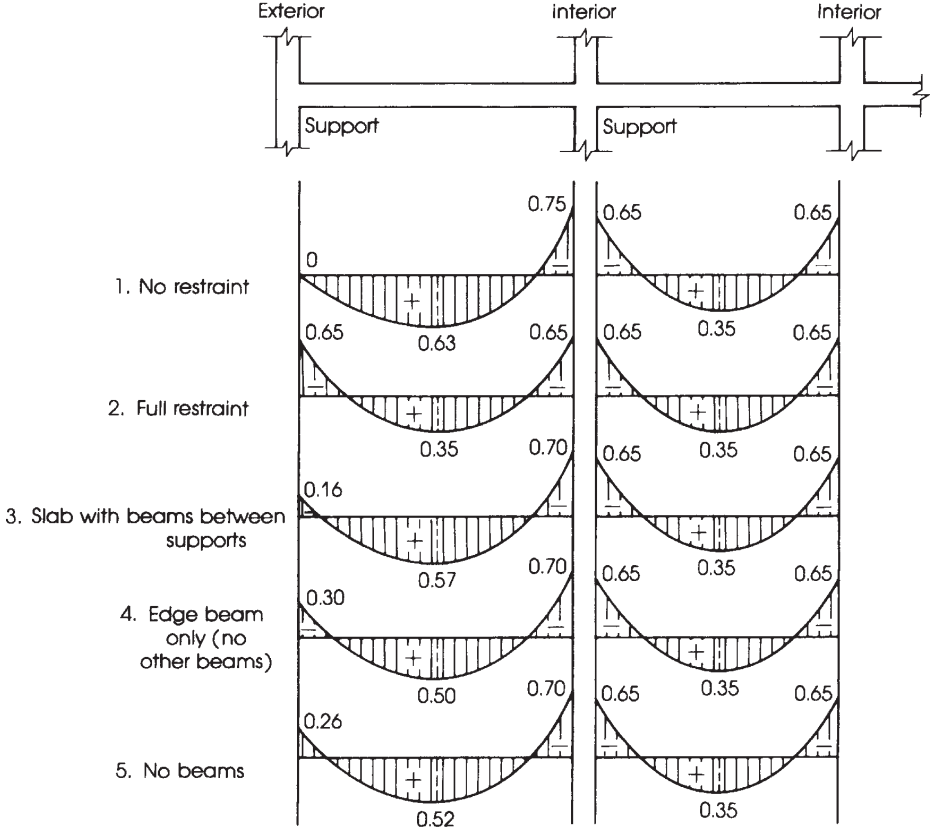
Figure 10. Répartition du moment statique total en moments de portée négatifs et positifs. (Nadim Hassoun et Akthem AI-Manaseer, “Théorie et conception du béton structurel”)

Répartition du moment pondéré total \({M_0}\) par travée en moments négatifs et positifs.

Une fois que \({M_0}\) a été calculé, il est temps d'attribuer la fraction des moments en positif et négatif dans chaque bande de conception, C'est, colonne et bandes médianes. Pour plus de clarté, figure 10 permet de spécifier le facteur approprié à prendre en compte dans la distribution du moment total.

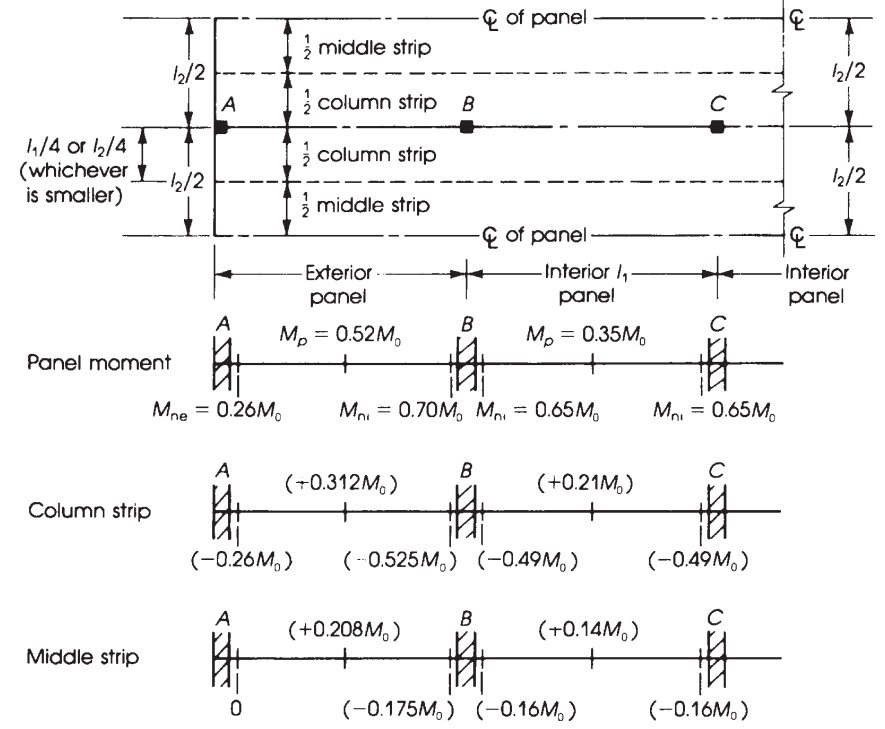
Figure 11. Largeur de l'ossature rigide équivalente et répartition des moments dans les dalles plates. (Nadim Hassoun et Akthem AI-Manaseer, “Théorie et conception du béton structurel”)

En utilisant les facteurs précédents indiqués dans la figure 10, on obtient dans le tableau suivant le moment ultime.

Direction longitudinale: \({M_0 = 189.97 kN-m}\)

Envergure (ES:Extérieur, EST:Intérieur)	Moment total (kN-m)	Moment de bande de colonne (kN-m)	Moment de la bande médiane (kN-m)
Extérieur Négatif ES	0.26M0=49,39	0.26M0=49,39	0
ES positif	0.52M0=98,78	0.31M0=58,89	0.21M0=39.89
ES négatif intérieur	0.70M0=132,98	0.53M0=100,68	0.17M0=32,29
SI positif	0.35M0=66,49	0.21M0=39.89	0.14M0=26,60
SI négatif	0.65M0=123,48	0.49M0=93.09	0.16M0=30.40

Avec le moment une fois distribué, il est temps de déterminer l'armature en acier à placer dans la dalle. Nous ne développerons qu'un seul calcul puis tous les résultats dans un tableau.

Moment dans la portée négative extérieure dans la bande de poteau, \({M_u = 49.39 kN-m}\)

• Section présumée à tension contrôlée. \({\phi_f = 0.9}\)
• Largeur de bande de colonne, \({b=2.0m}\)
• Zone de renfort en acier, \({A_s = frac{M_u}{\phi_ffois 0,9dfois fy}= frac{49.39kN-m}{0.9\fois 0.9(0.17m)\fois 420 MPa}=853.996 {mm}^ 2}\)
• \({\rho_{min} = 0.0018}\). Zone d'armature minimale en acier, \({UNE_{s,min}=rho_{min}\fois bfois d = 0.0018 \fois 2,0 m fois 0,17 m = 612 {mm}^ 2}\). Maintenant, vérifier si la section se comporte comme une tension contrôlée.
• \({a = frac{A_sfois f_y}{0.85\fois f'cfois b} = frac{853.996 {mm}^2fois 420 MPa}{0.85\fois 25 MPafois 2,0 m }= 8.439 mm}\)
• \({c = frac{a}{\bêta_1}= frac{8.439 mm}{0.85} = 9,929 mm }\)
• \({\varepsilon_t = (\frac{0.003}{c})\fois d – 0.003 = (\frac{0.003}{9.929mm})\fois 170mm – 0.003 = 0.048 > 0.005 }\) D'accord!, c'est une section à tension contrôlée!.

Envergure(ES:Extérieur, EST:Intérieur)	Moment de bande de colonne (kN-m)	\({UNE_{s,calc} ({mm}^ 2)}\)	\({UNE_{s,min} ({mm}^ 2)}\)	\({a (mm)}\)	\({c (mm)}\)	\({\varepsilon_t > 0.005}\)
Extérieur Négatif ES	49.39	853.996	612.0	8.439	9.929	0.048 > 0.005!
ES positif	58.89	1018.259	612.0	10.063	11.839	0.040 > 0.005!
ES négatif intérieur	100.68	1740.844	612.0	17.204	20.24	0.022 > 0.005!
SI positif	39.89	689.733	612.0	6.816	8.019	0.06 > 0.005!
SI négatif	93.09	1609.607	612.0	15.907	18.714	0.024 > 0.005!

Moment dans la portée positive extérieure dans la bande médiane, \({M_u = 39.89 kN-m}\)

• Section présumée à tension contrôlée. \({\phi_f = 0.9}\)
• Largeur de la bande médiane, \({b=2.0m}\)
• Zone de renfort en acier, \({A_s = frac{M_u}{\phi_ffois 0,9dfois fy}= frac{39.89kN-m}{0.9\fois 0.9(0.17m)\fois 420 MPa}=689.733 {mm}^ 2}\)
• \({\rho_{min} = 0.0018}\). Zone d'armature minimale en acier, \({UNE_{s,min}=rho_{min}\fois bfois d = 0.0018 \fois 2,0 m fois 0,17 m = 612 {mm}^ 2}\). Maintenant, vérifier si la section se comporte comme une tension contrôlée.
• \({a = frac{A_sfois f_y}{0.85\fois f'cfois b} = frac{689.766 {mm}^2fois 420 MPa}{0.85\fois 25 MPafois 2,0 m }= 6.816 mm}\)
• \({c = frac{a}{\bêta_1}= frac{6.816 mm}{0.85} = 8.019 mm }\)
• \({\varepsilon_t = (\frac{0.003}{c})\fois d – 0.003 = (\frac{0.003}{8.019mm})\fois 170mm – 0.003 = 0.0605 > 0.005 }\) D'accord!, c'est une section à tension contrôlée!.

Envergure(ES:Extérieur, EST:Intérieur)	Moment de la bande médiane (kN-m)	\({UNE_{s,calc} ({mm}^ 2)}\)	\({UNE_{s,min} ({mm}^ 2)}\)	\({a (mm)}\)	\({c (mm)}\)	\({\varepsilon_t > 0.005}\)
Extérieur Négatif ES	0	0.00	612.0	6.048	7.115	0.069 > 0.005!
ES positif	39.89	689.733	612.0	6.816	8.019	0.061 > 0.005!
ES négatif intérieur	32.29	558.322	612.0	6.048	7.115	0.069 > 0.005!
SI positif	26.60	459.937	612.0	6.048	7.115	0.069 > 0.005!
SI négatif	30.40	525.642	612.0	6.048	7.115	0.069 > 0.005!

Direction transversale: \({M_0 = 115.40 kN-m}\)

Envergure (ES:Extérieur, EST:Intérieur)	Moment total (kN-m)	Moment de bande de colonne (kN-m)	Moment de la bande médiane (kN-m)
Extérieur Négatif ES	0.26M0=30.00	0.26M0=30.00	0
ES positif	0.52M0=60.00	0.31M0=35,77	0.21M0=24.23
ES négatif intérieur	0.70M0=80,78	0.53M0=61.16	0.17M0=19.62
SI positif	0.35M0=40.39	0.21M0=24.23	0.14M0=16.16
SI négatif	0.65M0=75.01	0.49M0=56,55	0.16M0=18,46

Avec le moment une fois distribué, il est temps de déterminer l'armature en acier à placer dans la dalle. Nous ne développerons qu'un seul calcul puis tous les résultats dans un tableau.

Moment dans la portée négative extérieure dans la bande de poteau, \({M_u = 30.00 kN-m}\)

• Section présumée à tension contrôlée. \({\phi_f = 0.9}\)
• Largeur de bande de colonne, \({b=2.0m}\)
• Zone de renfort en acier, \({A_s = frac{M_u}{\phi_ffois 0,9dfois fy}= frac{30.00kN-m}{0.9\fois 0.9(0.17m)\fois 420 MPa}=518.726 {mm}^ 2}\)
• \({\rho_{min} = 0.0018}\). Zone d'armature minimale en acier, \({UNE_{s,min}=rho_{min}\fois bfois d = 0.0018 \fois 2,0 m fois 0,17 m = 612 {mm}^ 2}\). Maintenant, vérifier si la section se comporte comme une tension contrôlée.
• \({a = frac{A_sfois f_y}{0.85\fois f'cfois b} = frac{518.726 {mm}^2fois 420 MPa}{0.85\fois 25 MPafois 2,0 m }= 6.048 mm}\)
• \({c = frac{a}{\bêta_1}= frac{6.048 mm}{0.85} = 7,115 mm }\)
• \({\varepsilon_t = (\frac{0.003}{c})\fois d – 0.003 = (\frac{0.003}{7.115mm})\fois 170mm – 0.003 = 0.069 > 0.005 }\) D'accord!, c'est une section à tension contrôlée!.

Envergure(ES:Extérieur, EST:Intérieur)	Moment de bande de colonne (kN-m)	\({UNE_{s,calc} ({mm}^ 2)}\)	\({UNE_{s,min} ({mm}^ 2)}\)	\({a (mm)}\)	\({c (mm)}\)	\({\varepsilon_t > 0.005}\)
Extérieur Négatif ES	30.00	518.726	612.0	6.048	7.115	0.069 > 0.005!
ES positif	35.77	618.494	612.0	6.112	7.191	0.068 > 0.005!
ES négatif intérieur	61.16	1057.509	612.0	10.451	12.295	0.038 > 0.005!
SI positif	24.23	418.958	612.0	6.048	7.115	0.069 > 0.005!
SI négatif	56.55	977.799	612.0	9.663	11.368	0.042 > 0.005!

Moment dans la portée positive extérieure dans la bande médiane, \({M_u = 24.23 kN-m}\)

• Section présumée à tension contrôlée. \({\phi_f = 0.9}\)
• Largeur de bande de colonne, \({b=4.0m}\)
• Zone de renfort en acier, \({A_s = frac{M_u}{\phi_ffois 0,9dfois fy}= frac{24.23 kN-m}{0.9\fois 0.9(0.17m)\fois 420 MPa}=418.958 {mm}^ 2}\)
• \({\rho_{min} = 0.0018}\). Zone d'armature minimale en acier, \({UNE_{s,min}=rho_{min}\fois bfois d = 0.0018 \fois 4.0m fois 0.17m =1224 {mm}^ 2}\). Maintenant, vérifier si la section se comporte comme une tension contrôlée.
• \({a = frac{A_sfois f_y}{0.85\fois f'cfois b} = frac{1224 {mm}^2fois 420 MPa}{0.85\fois 25 MPafois 4,0 m }= 6.048 mm}\)
• \({c = frac{a}{\bêta_1}= frac{6.048 mm}{0.85} = 7.115 mm }\)
• \({\varepsilon_t = (\frac{0.003}{c})\fois d – 0.003 = (\frac{0.003}{7.115mm})\fois 170mm – 0.003 = 0.069 > 0.005 }\) D'accord!, c'est une section à tension contrôlée!.

Envergure(ES:Extérieur, EST:Intérieur)	Moment de la bande médiane (kN-m)	\({UNE_{s,calc} ({mm}^ 2)}\)	\({UNE_{s,min} ({mm}^ 2)}\)	\({a (mm)}\)	\({c (mm)}\)	\({\varepsilon_t > 0.005}\)
Extérieur Négatif ES	0.00	0.00	1224.00	6.048	7.115	0.069 > 0.005!
ES positif	24.23	418.958	1224.00	6.048	7.115	0.069 > 0.005!
ES négatif intérieur	19.62	339.247	1224.00	6.048	7.115	0.069 > 0.005!
SI positif	16.16	279.420	1224.00	6.048	7.115	0.069 > 0.005!
SI négatif	18.46	319.189	1224.00	6.048	7.115	0.069 > 0.005!

Si vous êtes nouveau chez SkyCiv, Inscrivez-vous et testez le logiciel vous-même!

Inscrivez-vous à SkyCiv!

Module de conception SkyCiv S3D

Dans cette section, nous décrivons le résultat de la conception à l'aide du module de conception de plaque inclus dans SkyCiv. Nous n'expliquons pas comment modéliser et analyser la structure (pour ces, voir les articles connexes sur ce sujet dans notre documentation: Comment modéliser une structure dans SkyCiv?, Comment appliquer des charges dans mon modèle de bâtiment? et Comment exécuter une analyse élastique linéaire?)

Il est pratique d'appliquer un maillage fin sur les dalles pour obtenir un résultat de conception précis. S'il vous plaît jeter un oeil à l'image suivante pour plus de clarté.

Figure 12. Maillage plus fin appliqué aux dalles

L'étape suivante consiste à exécuter le module de conception et à sélectionner les options qui calculent une zone d'armature en acier optimisée.

Figure 13. Définition des propriétés du béton de la dalle avant l'optimisation de la conception.

Figure 14 représente l'orientation des axes locaux de la plaque. Parce que l'axe local 3 est vers le bas, l' “Haut” est le fond, et la “bas” sera le top, prenant ainsi correctement les données de la conception.

Un autre fait important est le maillage de la dalle; il s'agit d'un élément plat carré aux dimensions en plan de 500mm x 500mm. SkyCiv S3D donne la zone de renforcement sous forme de valeur intégrée par élément fini. C'est à dire, si nous voulons obtenir la surface totale d'armature d'un poteau ou d'une bande médiane, nous devons calculer la valeur moyenne à partir du nombre d'éléments qui additionnent la largeur de la bande analysée. Par exemple, pour la bande de colonne, quatre éléments seront considérés (4×0.5m = 2m).

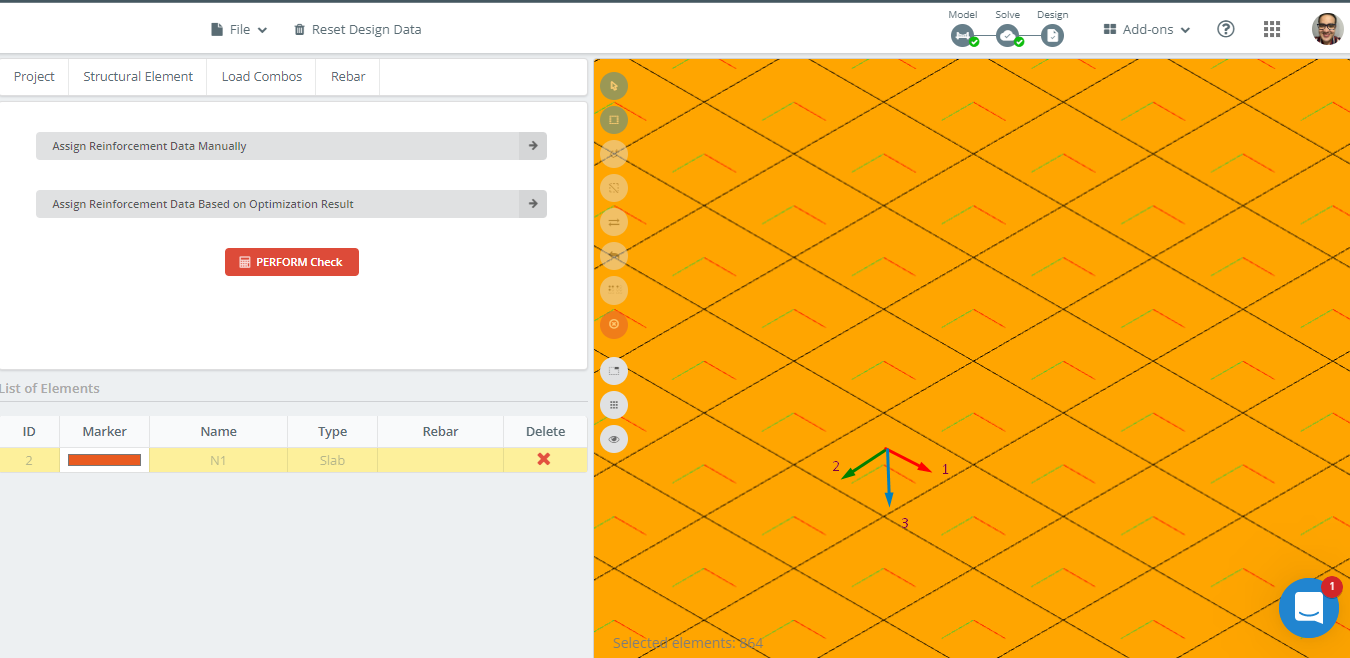
Figure 14. Orientation des axes locaux dans un exemple de dalle.

Première, nous analysons la zone de renforcement nécessaire le long de la direction longitudinale dans l'axe 1.

Bande de colonne

• Moment négatif extérieur (renfort supérieur): \({UNE_{s,Haut} =(119.09\fois 2 + 952.72 + 833.64 )\frac{{mm}^ 2}{m} \fois 0.50m = 1012.27 {mm}^ 2}\)
• Moment positif extérieur (renfort inférieur): \({UNE_{s,bot} = 4*463.90 \frac{{mm}^ 2}{m}\fois 0.50m = 927.80 {mm}^ 2}\)
• Moment négatif intérieur extérieur (renfort supérieur): \({UNE_{s,Haut} =(1071.82\fois 2 +714.54 \fois 2 )\frac{{mm}^ 2}{m} \fois 0.50m = 1786.36 {mm}^ 2}\)
• Moment positif intérieur(renfort inférieur): \({UNE_{s,bot} = 4*309.27 \frac{{mm}^ 2}{m}\fois 0.50m = 618.54 {mm}^ 2}\)
• Moment négatif intérieur (renfort supérieur): \({UNE_{s,Haut} =(714.54\fois 2 +952.73 \fois 2 )\frac{{mm}^ 2}{m} \fois 0.50m = 1667.27 {mm}^ 2}\)

Bande médiane

• Moment négatif extérieur (renfort supérieur): \({UNE_{s,Haut} =(119.09\fois 4)\frac{{mm}^ 2}{m} \fois 0.50m = 238.18 {mm}^ 2}\)
• Moment positif extérieur (renfort inférieur): \({UNE_{s,bot} = (463.90\fois 2 +412.36 \fois 2 ) \frac{{mm}^ 2}{m}\fois 0.50m = 876.26 {mm}^ 2}\)
• Moment négatif intérieur extérieur (renfort supérieur): \({UNE_{s,Haut} =(357.27\fois 2 +476.36 \fois 2 )\frac{{mm}^ 2}{m} \fois 0.50m = 833.63 {mm}^ 2}\)
• Moment positif intérieur(renfort inférieur): \({UNE_{s,bot} = 4*257.72 \frac{{mm}^ 2}{m}\fois 0.50m = 515.44 {mm}^ 2}\)
• Moment négatif intérieur (renfort supérieur): \({UNE_{s,Haut} =(357.27\fois 2 +476.36 \fois 2 )\frac{{mm}^ 2}{m} \fois 0.50m = 833.63 {mm}^ 2}\)

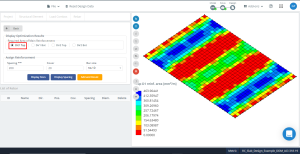
Figure 15. Résultats d'optimisation dans la direction “1” et le côté supérieur (La partie au fond, réellement).

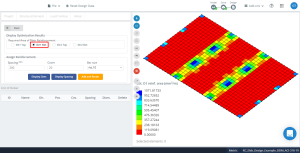
Figure 16. Résultats d'optimisation dans la direction “1” et la face inférieure (Face supérieure, réellement).

Ensuite, nous analysons la zone de renforcement nécessaire le long de la direction transversale dans l'axe 2.

Bande de colonne

• Moment négatif extérieur (renfort supérieur): \({UNE_{s,Haut} =(91.55\fois 2 + 457.73 + 549.28 )\frac{{mm}^ 2}{m} \fois 0.50m = 595.055 {mm}^ 2}\)
• Moment positif extérieur (renfort inférieur): \({UNE_{s,bot} = (269.68\fois 3+239.72) \frac{{mm}^ 2}{m}\fois 0.50m = 524.38 {mm}^ 2}\)
• Moment négatif intérieur extérieur (renfort supérieur): \({UNE_{s,Haut} =(823.92\fois 2 +549.28 +457.73)\frac{{mm}^ 2}{m} \fois 0.50m = 1327.43 {mm}^ 2}\)
• Moment positif intérieur(renfort inférieur): \({UNE_{s,bot} = (179.79\fois 3+149.82) \frac{{mm}^ 2}{m}\fois 0.50m = 344.60 {mm}^ 2}\)
• Moment négatif intérieur (renfort supérieur): \({UNE_{s,Haut} =(823.92\fois 2 +549.28 +457.73)\frac{{mm}^ 2}{m} \fois 0.50m = 1327.43 {mm}^ 2}\)

Bande médiane

• Moment négatif extérieur (renfort supérieur): \({UNE_{s,Haut} =(183.09\fois 2+91,55fois 6)\frac{{mm}^ 2}{m} \fois 0.50m = 457.74 {mm}^ 2}\)
• Moment positif extérieur (renfort inférieur): \({UNE_{s,bot} = (209.75\fois 2 +179.79 \fois 2 +149.82 \fois 4) \frac{{mm}^ 2}{m}\fois 0.50m = 689.18{mm}^ 2}\)
• Moment négatif intérieur extérieur (renfort supérieur): \({UNE_{s,Haut} =(274.64\fois 2+91,55fois 6)\frac{{mm}^ 2}{m} \fois 0.50m = 549.29 {mm}^ 2}\)
• Moment positif intérieur(renfort inférieur): \({UNE_{s,bot} = (119.86\fois 4 + 89.89\fois 4) \frac{{mm}^ 2}{m}\fois 0.50m = 419.50 {mm}^ 2}\)
• Moment négatif intérieur (renfort supérieur): \({UNE_{s,Haut} =(274.64\fois 2+91,55fois 6 )\frac{{mm}^ 2}{m} \fois 0.50m = 549.29 {mm}^ 2}\)

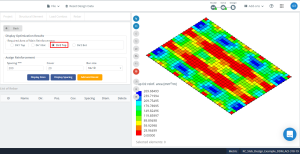
Figure 17. Résultats d'optimisation dans la direction “2” et le côté supérieur (La partie au fond, réellement).

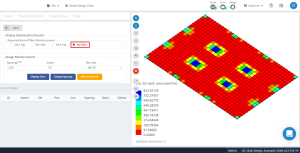
Figure 18. Résultats d'optimisation dans la direction “2” et la face inférieure (Face supérieure, réellement).

 

Comparaison des résultats

Le tableau suivant montre les résultats pour le DDM (“Méthode de conception directe”) et l'optimisation des barres d'armature en acier S3D.

Envergure (ES:Extérieur, EST:Intérieur)	Bande de colonne (Conception S3D) \({Comme ({mm}^ 2)}\)	Bande de colonne (ACI-318 DDM) \({Comme ({mm}^ 2)}\)	% Diff	Bande médiane (Conception S3D) \({Comme ({mm}^ 2)}\)	Bande médiane (ACI-318 DDM) \({Comme ({mm}^ 2)}\)	% Diff
Extérieur Négatif ES	1012.27	853.996	15.636	238.18	0 (612.0)	100.00
ES positif	927.80	1018.259	9.75	876.26	689.733	21.287
ES négatif intérieur	1786.36	1740.844	2.48	833.63	558.322 (612.0)	26.586
SI positif	618.54	689.733	11.51	515.44	459.937 (612.0)	18.734
SI négatif	1667.27	1609.607	3.459	833.63	525.642 (612.0)	26.586

Direction transversale

Envergure (ES:Extérieur, EST:Intérieur)	Bande de colonne (Conception S3D) \({Comme ({mm}^ 2)}\)	Bande de colonne (ACI-318 DDM) \({Comme ({mm}^ 2)}\)	% Diff	Bande médiane (Conception S3D) \({Comme ({mm}^ 2)}\)	Bande médiane (ACI-318 DDM) \({Comme ({mm}^ 2)}\)	% Diff
Extérieur Négatif ES	595.055	518.726	12.827	457.74	0 (1224)	100.00
ES positif	524.38	618.494	17.948	689.18	418.958	39.209
ES négatif intérieur	1327.43	1057.509	20.334	549.29	339.247	38.239
SI positif	344.60	418.958	21.578	419.50	279.42	33.392
SI négatif	1327.43	977.799	26.339	549.29	319.189	41.891

Conclusion

Nous avons démontré dans cet article que le module SkyCiv pour la conception des plaques calcule l'armature en acier pour plier la dalle conformément au code ACI-318-19. Comparer les résultats de l'analyse dans les bandes de colonne, où en raison de leur rigidité relative, les moments sont très concentrés, les différences entre les calculs manuels et l'optimisation par S3D arrondissent une valeur de 10 – 15%. Cette praticité indique une excellente adéquation entre les procédures d'analyse et de conception.

Pour les bandes intermédiaires, les résultats diffèrent un peu plus car le code n'attribue le reste du moment qu'après avoir pris les bandes de colonnes correspondantes. Cela aura un impact sur le match lorsque nous le comparerons avec l'analyse du logiciel, ce qui est plus précis.

Nouveau sur SkyCiv? Inscrivez-vous et essayez le logiciel vous-même!

Inscrivez-vous à SkyCiv!