Comment calculer la capacité de charge ultime d'un seul pieu

Capacité de charge

---

L'évaluation de la capacité de charge ultime d'un seul pieu est l'un des aspects les plus importants de la conception du pieu, et peut parfois être compliqué. Cet article passera en revue les équations qui régissent la conception à un seul pieu ainsi qu'un exemple.

Pour comprendre facilement le mécanisme de transfert de charge d'une seule pile, imaginez un pieu en béton de longueur L de diamètre D, tel qu'illustré à la figure 1.

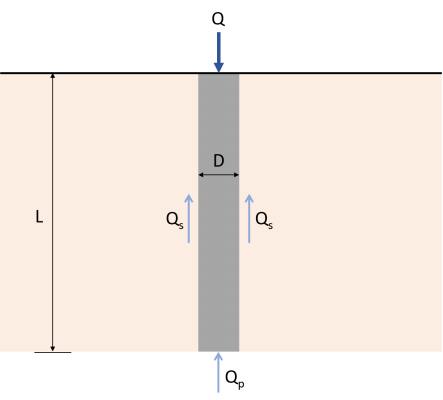
Figure 1: Mécanisme de transfert de charge pour pieux

La charge Q appliquée sur le pieu doit être transférée directement sur le sol en bas du pieu. Une partie de cette charge sera résistée par les côtés de la pile en utilisant quelque chose appelé “Frottement cutané” développé le long de l'arbre (Q_s), et le reste sera résisté par le sol sur lequel repose la pile (Q_p). Par conséquent, la capacité de charge ultime (Qu) d'une pile doit être donnée par l'équation (1). Il existe plusieurs méthodes disponibles pour estimer les valeurs de Q_p et Q_s.

\( {Q}_{u} = {Q}_{p} + {Q}_{s} \) (1)

Q_u = Capacité de charge ultime

Q_p = Capacité de charge en bout

Q_s = Résistance au frottement cutané

Vous voulez essayer le logiciel Foundation Design de SkyCiv? Notre outil gratuit permet aux utilisateurs d'effectuer des calculs de charge sans aucun téléchargement ni installation!

Calculatrice de conception de fondation

Capacité portante d'extrémité, Q_p

---

La capacité portante finale est théoriquement la charge maximale par unité de surface qui peut être supportée par le sol en palier, sans échec. L'équation suivante de Karl Von Terzaghi, le père de la mécanique des sols, est l'une des premières et des plus couramment utilisées pour évaluer la capacité portante ultime des fondations. L'équation de Terzaghi pour la capacité portante ultime peut être exprimée comme:

\( {q}_{u} = (c × {N}_{c}) + (q × {N}_{q}) + (\frac{1}{2} × γ × B × {N}_{c}) \) (2)

q_u = Capacité portante ultime

c = Cohésion du sol

q = pression effective du sol

γ = poids unitaire du sol

B = Profondeur ou diamètre de la section transversale

N_c, N_q, N_c = Facteurs de roulement

Depuis q_u est en termes de charge par unité de surface ou de pression, la multiplier par la section transversale du pieu donnera la capacité de charge en bout (Q_p) de la pile. La valeur résultante du dernier terme de l'équation 2 est négligeable en raison d'une largeur de poil relativement petite, donc, il peut être supprimé de l'équation. C'est à dire, la capacité de charge finale finale du pieu peut être exprimée comme indiqué dans l'équation (3). Cette version modifiée de l'équation de Terzaghi est utilisée dans le module SkyCiv Foundation lors de la conception de pieux.

\( {Q}_{p} = {A}_{p} × [(c × {N}_{c}) + (q × {N}_{q}) ] \) (3)

A_p = Aire transversale du pieu

Facteurs de roulement N_c et n_q sont non dimensionnels, dérivé empiriquement, et sont des fonctions de l'angle de frottement du sol (Phi). Les chercheurs ont déjà effectué les calculs nécessaires pour trouver les facteurs de roulement. Le tableau 1 résume les valeurs de N_q selon Naval Facilities Engineering Command (NAVFAC DM 7.2, 1984). La valeur de N_c est approximativement égal à 9 pour pieux sous sols argileux.

Facteur de roulement (Nq)
Angle de friction (Ø)	26	28	30	31	32	33	34	35	36	37	38	39	40
Pieux entraînés	10	15	21	24	29	35	42	50	62	77	86	120	145
Piles ennuyées	5	8	10	12	14	17	21	25	30	38	43	60	72

Le tableau 1: N_q valeurs de NAVFAC DM 7.2

Capacité de résistance au frottement cutané, Q_s

---

La résistance au frottement cutané des pieux est développée sur toute la longueur du pieu. En général, la résistance au frottement d'un pieu est exprimée par:

\( {Q}_{s} = ∑ (p × ΔL × f) \) (4)

p = Périmètre de la pile

ΔL = longueur de pieu incrémentale sur laquelle p et f sont pris

f = résistance de frottement de l'unité à n'importe quelle profondeur

Estimation de la valeur de la résistance de frottement unitaire (F) nécessite plusieurs facteurs importants à prendre en compte, comme la nature de l'installation des pieux et la classification du sol. Équations (5) et (6) montre la méthode de calcul pour trouver l'unité de résistance au frottement des pieux dans les sols sableux et argileux, respectivement. les tables 2 et 3 présenter le coefficient de pression de terre efficace recommandé (K) et l'angle de frottement du tas de terre (δ »), selon NAVFAC DM7.2.

Pour les sols sableux:

\( f = K × σ ’× tan(δ ») \) (5)

K = coefficient de pression effective des terres

σ’ = Contrainte verticale effective à la profondeur considérée

ré’ = Angle de frottement sol-pile

Pour les sols argileux:

\( f = α × c \) (6)

α = facteur d'adhésion empirique

Angle de frottement sol-pile (δ »)
Type de pile	ré’
Pile d'acier	20º
Pile de bois	3/4 × Φ
Pile de béton	3/4 × Φ

Le tableau 2: Valeurs d'angle de frottement sol-pieu (NAVFAC DM7.2, 1984)

Coefficient de pression de terre latérale (K)
Type de pile	Pile de compression	Pile de tension
Pieux en H enfoncés	0.5-1.0	0.3-0.5
Pieux à déplacement entraîné (rond, rectangulaire)	1.0-1.5	0.6-1.0
Pieux à déplacement entraîné (effilé)	1.5-2.0	1.0-1.3
Pieux projetés	0.4-0.9	0.3-0.6
Pieux forés (<24″ Diamètre)	0.7	0.4

Le tableau 3: Coefficient de pression de terre latérale (K) Valeurs (NAVFAC DM7.2, 1984)

Facteur d'adhésion (une)
c / pa	une
≤ 0.1	1.00
0.2	0.92
0.3	0.82
0.4	0.74
0.6	0.62
0.8	0.54
1.0	0.48
1.2	0.42
1.4	0.40
1.6	0.38
1.8	0.36
2.0	0.35
2.4	0.34
2.8	0.34

Remarque: p_a = pression atmosphérique ≈ 100 kN / m²

Le tableau 4: Valeurs du facteur d'adhésion (Terzaghi, Picorer, et Mesri, 1996)

Exemple: Calcul de la capacité des pieux dans le sable

---

Un pieu en béton de 12 mètres de long d'un diamètre de 500 mm est enfoncé dans plusieurs couches de sable sans eau souterraine. Trouvez la capacité de charge ultime (Q_u) de la pile.

Détails
Section
Diamètre	500 mm
Longueur	12 m
Propriétés de la couche 1-sol
Épaisseur	5 m
Unité de poids	17.3 kN / m3
Angle de friction	30 Degrés
Cohésion	0 kPa
Table des eaux souterraines	Pas présent
Propriétés du sol de la couche 2
Épaisseur	7 m
Unité de poids	16.9 kN / m3
Angle de friction	32 Degrés
Cohésion	0 kPa
Table des eaux souterraines	Pas présent

Étape 1: Calculer la capacité de charge en bout (Q_p).

Au bout de la pile:

A_p = (π / 4) × D² = (π / 4) × 0.5²

A_p = 0.196 m²

c = 0 kPa

θ = 32 °

N_q = 29 (De la table 1)

Pression efficace du sol (q):

q = (c₁ × t₁) + (c₂ × t₂) = (5 m × 17.3 kN / m³) + (7 m × 16.9 kN / m³)

q = 204.8 kPa

Ensuite, utilisez l'équation (3) pour la capacité de charge en bout:

Q_p = A_p × [(c × N_c) + (q × N_q)]

Q_p = 0.196 m² × ( 204.8 KPa × 29)

Q_p = 1,164.083 kN

Étape 2: Calculez la résistance au frottement cutané (Q_s).

Utiliser des équations (4) et (5), calculer le frottement cutané par couche de sol.

Q_s = ∑ (p × ΔL × f)

p = π × D = π × 0.5 m

p = 1.571 m

Couche 1:

ΔL = 5 m

F₁ = K × σ’₁× bronzage(δ »)

K = 1.25 (Le tableau 3)

ré’ = 3/4 × 30º

ré’ = 22,50º

σ’₁ = γ₁ × (0.5 × t₁) = 17.3 kN / m³ × (0.5 × 5 m)

σ’₁ = 43.25 kN / m²

F₁ = 1.25 × 43.25 kN / m² × bronzage(22.50º)

F₁ = 22.393 kN / m²

Q_s1 = p × ΔL × f₁ = 1.571 m × 5 m × 22.393 kN / m²

Q_s1 = 175.897 kN

Couche 2:

ΔL = 7 m

F₂ = K × σ’₂× bronzage(δ »)

K = 1.25 (Le tableau 3)

ré’ = 3/4 × 32º

ré’ = 24º

σ’₂ = (c₁ × t₁) + [c₂ × (0.5 × t₂)] = (17.3 kN / m³ × 5 m) + [16.9 kN / m³ ×(0.5 × 7 m)]

σ’₂ = 145.65 kN / m²

F₂ = 1.25 × 145.65 kN / m² × bronzage(24º)

F₂ = 81.059 kN / m²

Q_s2 = p × ΔL × f₂ = 1.571 m × 7 m × 81.059 kN / m²

Q_s2 = 891.406 kN

Résistance totale au frottement cutané:

Q_s = Q_s1+ Q_s2 = 175.897 kN + 891.406 kN

Q_s = 1,067.303 kN

Étape 3: Calculez pour la capacité de charge ultime (Q_u).

Q_u = Q_p+ Q_s = 1,164.083 kN + 1,067.303 kN

Q_u = 2,231.386 kN

Exemple 2: Calcul de la capacité des pieux en argile

---

Considérez un 406 pieu en béton de mm de diamètre d'une longueur de 30 m encastré dans une couche, argile saturée. Trouvez la capacité de charge ultime (Q_u) de la pile.

Détails
Section
Diamètre	406 mm
Longueur	30 m
Propriétés de la couche 1-sol
Épaisseur	10 m
Unité de poids	8 kN / m3
Angle de friction	0º
Cohésion	30 kPa
Table des eaux souterraines	5 m
Propriétés du sol de la couche 2
Épaisseur	10 m
Unité de poids	19.6 kN / m3
Angle de friction	0º
Cohésion	0 kPa
Table des eaux souterraines	Entièrement submergé

Étape 1: Calculer la capacité de charge en bout (Q_p).

Au bout de la pile:

A_p = (π / 4) × D²= (π / 4) × 0.406²

A_p = 0.129 m²

c = 100 kPa

N_c = 9 (Valeur typique de l'argile)

Q_p = (c × N_c) × A_p = (100 kPa × 9) × 0.129 m²

Q_p = 116.1 kN

Étape 2: Calculez la résistance au frottement cutané (Q_s).

Utiliser des équations (4) et (6), calculer le frottement cutané par couche de sol.

Q_s = ∑ (p × ΔL × f)

p = π × D = π × 0.406 m

p = 1.275 m

Couche 1:

ΔL = 10 m

une₁ = 0.82 (Le tableau 4)

c₁ = 30 kPa

F₁= α₁ × c₁ = 0.82 × 30 kPa

F₁ = 24.6 kN / m²

Q_s1 = p × ΔL × f₁ = 1.275 m × 10 m × 24.6 kN / m²

Q_s1 = 313.65 kN / m²

Couche 2:

ΔL = 20 m

une₂= 0.48 (Le tableau 4)

c₂ = 100 kPa

F₂ = α₂ × c₂ = 0.48 × 100 kPa

F₂ = 48 kN / m²

Q_s2 = p × ΔL × f₂ = 1.275 m × 20 m × 48 kN / m²

Q_s2 = 1,224 kN / m²

Résistance totale au frottement cutané:

Q_s = Q_s1+ Q_s2 = 313.65 kN + 1224 kN

Q_s = 1,537.65 kN

Étape 3: Calculez pour la capacité de charge ultime (Q_u).

Q_u = Q_p+ Q_s = 116.1 kN + 1537.65 kN

Q_u = 1,653.75 kN

Vous voulez essayer le logiciel Foundation Design de SkyCiv? Notre outil gratuit permet aux utilisateurs d'effectuer des calculs de charge sans aucun téléchargement ni installation!

Calculatrice de conception de fondation

Références:

• Le, B.M. (2007). Principes de l'ingénierie des fondations (7e édition). Ingénierie globale
• Rajapakse, R. (2016). Conception de pieux et règle de construction du pouce (2nd édition). Elsevier Inc.
• Tomlinson, M.J. (2004). Conception de pieux et pratique de construction (4e édition). E & FN Spon.