Exemple de conception de plaque de base en utilisant comme 4100:2020 et AS 3600:2018
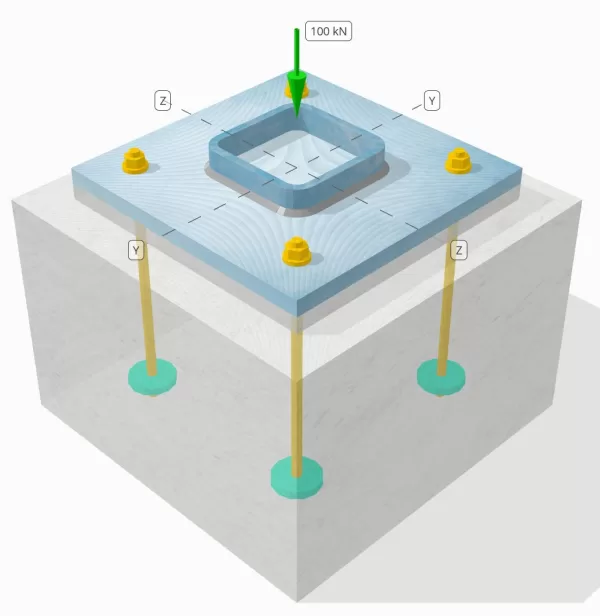
Déclaration de problème:
Déterminez si la connexion de la colonne à base de colonne conçue est suffisante pour une charge de compression de 100 kN.
Données données:
Colonne:
Section colonne: 50×10 SHS
Zone de colonne: 5260 mm2
Matériau de colonne: AS / NZS 1163 Grain. C350
Plaque de base:
Dimensions de la plaque de base: 350 millimètre x 350 mm
Épaisseur de plaque de base: 20 mm
Matériau de plaque de base: AS / NZS 3678 Grain. C250
Jointoyer:
Épaisseur de coulis: 20 mm
Béton:
Dimensions du béton: 450 millimètre x 450 mm
Épaisseur de béton: 300 mm
Matériau en béton: N28
Soudures:
Taille de soudure: 6 mm
Classification du métal de remplissage: E43xx
Charge de compression transférée par les soudures uniquement? OUI
Calculs étape par étape:
Vérifier #1: Calculer la capacité de roulement en béton
Commencer, Nous déterminons le zones de roulement par AS 3600:2018 Clause 12.6:
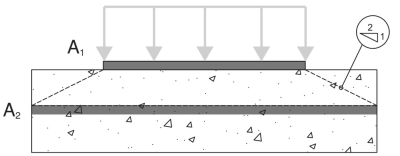
A1 - zone de roulement de plaque de base
A2 - Zone de roulement de support en béton, projeté à un 2:1 pente
\(
A_1 = l_{pb} B_{pb} = 350 \, \texte{mm} \fois 350 \, \texte{mm} = 122500 \, \texte{mm}^ 2
\)
\(
A_2 = n_{A2} B_{A2} = 450 \, \texte{mm} \fois 450 \, \texte{mm} = 202500 \, \texte{mm}^ 2
\)
De là, on calcule le capacité de roulement en béton, exprimé comme une force équivalente. Nous utilisons Guide de conception ASI 07 1st Ed. Section 9.1 comme référence.
\(
\phi n_c = min gauche( \phi 0.9 \la gauche( F’_C Right) A_1 sqrt{\frac{A_2}{A_1}}, \phi 1.8 \la gauche( F’_C Right) A_1 droite)
\)
\(
\phi n_c = min gauche( 0.6 \fois 0.9 \fois gauche( 28 \, \texte{MPa} \droite) \fois 122500 \, \texte{mm}^ 2 Times sqrt{\frac{202500 \, \texte{mm}^ 2}{122500 \, \texte{mm}^ 2}}, 0.6 \fois 1.8 \fois gauche( 28 \, \texte{MPa} \droite) \fois 122500 \, \texte{mm}^ 2 à droite)
\)
\(
\non -n_c = 2381.4 \, \texte{kN}
\)
Puisque 100 kN <2381.4 kN, l' La capacité de roulement en béton est suffisante.
Vérifier #2: Calculer la capacité de soudure
Pour évaluer la capacité de soudure, Nous déterminons d'abord le Longueur totale de soudure Basé sur les dimensions de la colonne:
\(
L_{\texte{souder}} = 2 \la gauche( b_{\texte{col}} – 2 r_{\texte{col}} – 2 t_{\texte{col}} \droite) + 2 \la gauche( ré_{\texte{col}} – 2 r_{\texte{col}} – 2 t_{\texte{col}} \droite)
\)
\(
L_{\texte{souder}} = 2 \fois gauche( 150 \, \texte{mm} – 2 \fois 15 \, \texte{mm} – 2 \fois 10 \, \texte{mm} \droite) + 2 \fois gauche( 150 \, \texte{mm} – 2 \fois 15 \, \texte{mm} – 2 \fois 10 \, \texte{mm} \droite) = 400 \, \texte{mm}
\)
Avec ça, Nous pouvons calculer le contrainte par unité de longueur de soudure, en supposant le 100 La charge KN est uniformément distribuée:
\(
v ^ * _ w = frac{N_x}{L_{\texte{souder}}} = frac{100 \, \texte{kN}}{400 \, \texte{mm}} = 0.25 \, \texte{kN / mm}
\)
Après ça, Nous déterminons le Capacité de soudure par unité de longueur utilisant AS 4100:2020 Clause 9.6.3.10:
\(
\Phi v_w = phi 0.6 F_{votre} E_w k_r = 0.8 \fois 0.6 \fois 430 \, \texte{MPa} \fois 4.243 \, \texte{mm} \fois 1 = 0.87576 \, \texte{kN / mm}
\)
Puisque 0.87576 kN / mm < 0.25 kN / mm, l' La capacité de soudure est suffisante.
Vérifier #3: Calculer la capacité de rendement en flexion de la plaque de base due à la charge de compression
La capacité de flexion de la plaque de base dépend de ses dimensions. Si la plaque est trop large, il nécessitera un matériau plus épais. La sélection de la bonne taille de plaque de base pour une charge donnée nécessite une expérience, et effectuer plusieurs calculs peut prendre du temps. Ce logiciel Logiciel de conception de plaques de base Skyciv simplifie ce processus, permettant une modélisation et une analyse rapides et efficaces en quelques secondes seulement.
Nous utilisons Guide de conception ASI 07, 1St Ed., Le tableau 7 Pour vérifier la capacité de rendement en flexion de la plaque de base. Première, Nous déterminons le kx facteur.
\(
k_x = 1.65 \la gauche( \frac{\sqrt{L_{pb} B_{pb}}}{b_{\texte{col}}} \droite) = 1.65 \fois gauche( \frac{\sqrt{350 \, \texte{mm} \fois 350 \, \texte{mm}}}{150 \, \texte{mm}} \droite) = 3.85
\)
Prochain, Nous calculons la résistance au roulement en béton en termes de stress sur la zone. Se référer à Vérifier #1 Pour la capacité de roulement calculée.
\(
\Phi f_b = frac{\non -n_c}{L_{pb} B_{pb}} = frac{2381.4 \, \texte{kN}}{350 \, \texte{mm} \fois 350 \, \texte{mm}} = 19.44 \, \texte{MPa}
\)
Nous utilisons ensuite cette valeur pour obtenir le X facteur.
\(
X = frac{4 N_c ^ *}{\Phi F_B (2 b_{\texte{col}})^ 2} = frac{4 \fois 100 \, \texte{kN}}{19.44 \, \texte{MPa} \fois (2 \fois 150 \, \texte{mm})^ 2} = 0.22862
\)
Maintenant, Laissez-nous utiliser le calculé kx et X facteurs pour évaluer le λ (lambda) facteur.
\(
\lambda = min gauche( \frac{k_x sqrt{X}}{1 + \sqrt{1 – X}}, 1.0 \droite) = min gauche( \frac{3.85 \fois sqrt{0.22862}}{1 + \sqrt{1 – 0.22862}}, 1 \droite) = 0.98008
\)
Nous calculons ensuite la longueur en porte-à-faux de la plaque de base subissant la charge de roulement. Selon Guide de conception ASI 07, 1St Ed., Sections 6.1 et 9.1–9.2, La longueur en porte-à-faux est comme indiqué:
\(
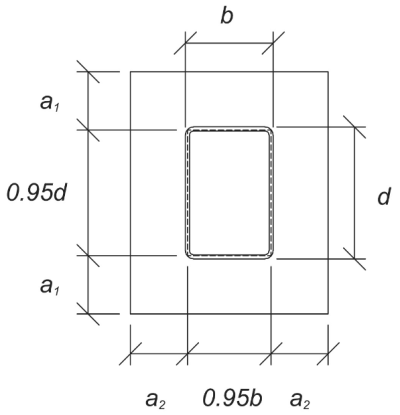
l = max gauche( \frac{L_{pb} – 0.95 ré_{\texte{col}}}{2}, \frac{B_{pb} – 0.95 b_{\texte{col}}}{2}, \lambda 0.306 \sqrt{ré_{\texte{col}} b_{\texte{col}}} \droite)
\)
\(
l = max gauche( \frac{350 \, \texte{mm} – 0.95 \fois 150 \, \texte{mm}}{2}, \frac{350 \, \texte{mm} – 0.95 \fois 150 \, \texte{mm}}{2}, 0.98008 \fois 0.306 \fois sqrt{150 \, \texte{mm} \fois 150 \, \texte{mm}} \droite)
\)
\(
l = 103.75 \, \texte{mm}
\)
Considérant cette section critique de la plaque de base, Calcularons la détente de la flexion. Ceci est une équation réarrangée de Guide de conception ASI 07, 1St Ed., Section 9.2, en référence à Section 6.1.
\(
f ^ * = frac{2 N_x l ^ 2}{B_{pb} L_{pb} (t_{pb})^ 2}
\)
\(
f ^ * = frac{2 \fois 100 \, \texte{kN} \fois 103.75 \, \texte{mm}^ 2}{350 \, \texte{mm} \fois 350 \, \texte{mm} \fois (20 \, \texte{mm})^ 2} = 43.935 \, \texte{MPa}
\)
La dernière étape consiste à calculer la capacité de rendement de la plaque de base en utilisant AS 4100:2020, Clause 5.2.1.
\(
\Phi f_y = phi f_{y_{pb}} = 0.9 \fois 250 \, \texte{MPa} = 225 \, \texte{MPa}
\)
Puisque 43.935 MPa < 225 MPa, l' La capacité de flexion de la plaque de base est suffisante.
Résumé de la conception
Le logiciel de conception de la plaque de base SkyCiv peut générer automatiquement un rapport de calcul étape par étape pour cet exemple de conception. Il fournit également un résumé des contrôles effectués et de leurs ratios résultants, rendre les informations faciles à comprendre en un coup d'œil. Vous trouverez ci-dessous un échantillon de tableau de résumé, qui est inclus dans le rapport.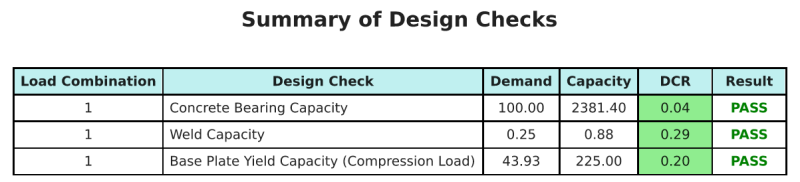
Rapport d'échantillon de skyciv
Cliquez ici Pour télécharger un exemple de rapport.
Logiciel d'achat de plaques de base
Achetez la version complète du module de conception de la plaque de base seul sans aucun autre module Skyviv. Cela vous donne un ensemble complet de résultats pour la conception de la plaque de base, y compris des rapports détaillés et plus de fonctionnalités.
