Exemple de conception de plaque de base en utilisant EN 1993-1-8-2005, EN 1993-1-1-2005 et EN 1992-1-1-2004
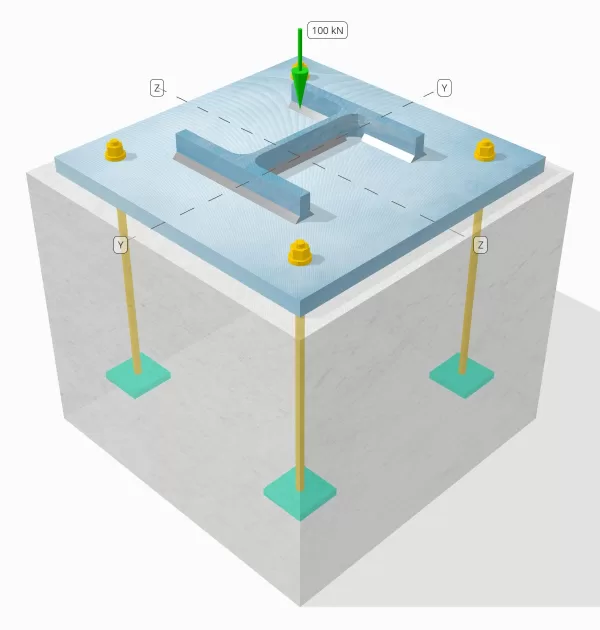
Déclaration de problème
Déterminez si la connexion de la colonne à base de colonne conçue est suffisante pour une charge de compression de 100 kN.
Données données
Colonne:
Section colonne: IL 200 B
Zone de colonne: 7808 mm2
Matériau de colonne: S235
Plaque de base:
Dimensions de la plaque de base: 400 millimètre x 400 mm
Épaisseur de plaque de base: 20 mm
Matériau de plaque de base: S235
Jointoyer:
Épaisseur de coulis: 20 mm
Béton:
Dimensions du béton: 450 millimètre x 450 mm
Épaisseur de béton: 380 mm
Matériau en béton: C20 / 25
Soudures:
Charge de compression transférée par les soudures uniquement? NON
Modèle dans l'outil gratuit SkyCiv
Modélisez la conception de la plaque de base ci-dessus à l'aide de notre outil en ligne gratuit dès aujourd'hui.! Aucune inscription requise.
Calculs étape par étape
Vérifier #1: Calculer la capacité de soudure
Puisque la charge de compression n'est pas transférée par les soudures seules, Une surface de roulement de contact appropriée est nécessaire pour garantir que la charge est transférée par roulement. Se référer à EN 1090-2:2018 Clause 6.8 pour la préparation du roulement de contact.
Aussi, Utiliser la taille de la soudure minimale spécifié dans Eurocode.
Vérifier #2: Calculer la capacité de roulement en béton et la capacité de rendement de la plaque de base
La première étape consiste à déterminer la résistance à la compression de la conception de l'articulation, qui dépend de la géométrie du soutien (le béton) et la géométrie de la zone chargée (assiette de base).
Nous commençons par calculer le facteur alpha, qui explique la diffusion de la force concentrée dans la fondation.
Selon EN 1992-1-1:2004, Clause 6.7, Le coefficient alpha est le rapport de la zone chargée à la zone de distribution maximale, qui a une forme similaire à la zone chargée.
Nous utiliserons l'équation de Partie 6.1 des bâtiments en acier à plusieurs étages 5 par Arcelor Mittal, Transporteur de Peiner, et Corus Pour calculer le facteur alpha.
\(
\alpha = min gauche(
1 + \frac{t_{\texte{concurrence}}}{\max(L_{\texte{pb}}, B_{\texte{pb}})},
1 + 2 \la gauche( \frac{e_h}{L_{\texte{pb}}} \droite),
1 + 2 \la gauche( \frac{E_B}{B_{\texte{pb}}} \droite),
3
\droite)
\)
\(
\alpha = min gauche(
1 + \frac{380 \, \texte{mm}}{\max(400 \, \texte{mm}, 400 \, \texte{mm})},
1 + 2 \la gauche( \frac{25 \, \texte{mm}}{400 \, \texte{mm}} \droite),
1 + 2 \la gauche( \frac{25 \, \texte{mm}}{400 \, \texte{mm}} \droite),
3
\droite)
\)
\(
\alpha = 1.125
\)
où,
\(
e_h = frac{L_{\texte{concurrence}} – L_{\texte{pb}}}{2} = frac{450 \, \texte{mm} – 400 \, \texte{mm}}{2} = 25 \, \texte{mm}
\)
\(
e_b = frac{B_{\texte{concurrence}} – B_{\texte{pb}}}{2} = frac{450 \, \texte{mm} – 400 \, \texte{mm}}{2} = 25 \, \texte{mm}
\)
Une fois la géométrie définie, Nous déterminerons ensuite la résistance à la compression du béton en utilisant EN 1992-1-1:2004, Eq. 3.15.
\(
F_{CD} = frac{\alpha_{cc} F_{afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués}}{\Gamma_c} = frac{1 \fois 20 \, \texte{MPa}}{1.5} = 13.333 \, \texte{MPa}
\)
Prochain, Nous supposons une valeur pour le coefficient bêta. Puisque le coulis est présent, La valeur bêta peut être 2/3. Nous calculerons la résistance à la conception de l'articulation à l'aide des formules combinées de EN 1993-1-8:2005 Eq. 6.6, et EN 1992-1-1:2004 Eq. 6.63.
\(
F_{afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués} = beta alpha f_{CD} = 0.66667 \fois 1.125 \fois 13.333 \, \texte{MPa} = 10 \, \texte{MPa}
\)
La deuxième partie consiste à calculer la capacité de rendement de la plaque de base.
Puisque nous avons déjà la force de conception de la connexion, Nous l'utiliserons pour déterminer la plus petite distance en porte-à-faux de la plaque de base qui éprouve la charge de roulement complète. Nous ferons référence au Sci P358 Exemple sur page 243 et EN 1993-1-1:2005 Clause 6.2.5.
\(
c = t_{\texte{pb}} \sqrt{\frac{F_{y_{\texte{pb}}}}{3 F_{afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués} \gamma_{M0}}} = 20 \, \texte{mm} \fois sqrt{\frac{225 \, \texte{MPa}}{3 \fois 10 \, \texte{MPa} \fois 1}} = 54.772 \, \texte{mm}
\)
Nous utiliserons cette dimension pour calculer la zone efficace de la plaque de base. Le «C’ dimension que nous avons calculée peut se chevaucher ou ne pas se chevaucher près de la bride. Si ça chevauche, Nous supposerons que la section est une section rectangulaire. S'il ne chevauche pas, Nous prendrons la forme de la colonne.
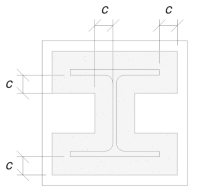
Sans chevauchement
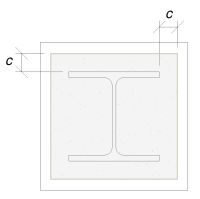
Avec chevauchement
Nous avons déterminé que le «C’ La dimension ne chevauche pas. Par conséquent, utilisant Sci P358 PG. 243, la zone efficace est:
\(
A_e = 4c ^ 2 + P_{\texte{col}}c + UNE_{\texte{col}} = 4 \Times 54.772 ^ 2 \, \texte{mm}^ 2 + 1182 \, \texte{mm} \fois 54.772 \, \texte{mm} + 7808 \, \texte{mm}À partir de l'élévation du sol générée à partir des élévations Google 84549 \, \texte{mm}^ 2
\)
Il est important de noter que la zone efficace ne doit pas être inférieure à la zone de la plaque de base.
Ensuite, nous utiliserons EN 1993-1-8:2005 Eq. 6.6, et EN 1992-1-1:2004, Eq. 6.63 Pour calculer la résistance à la conception de la connexion de la plaque de base.
\(
N_{Rd} = gauche( \min(A_e, A_0) \droite) F_{afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués} = gauche( \min(84549 \, \texte{mm}^ 2, 160000 \, \texte{mm}^ 2) \droite) \fois 10 \, \texte{MPa} = 845.49 \, \texte{kN}
\)
Puisque 845.49 kN > 100 kN, Le design est suffisant!
Résumé de la conception
Le logiciel de conception de la plaque de base SkyCiv peut générer automatiquement un rapport de calcul étape par étape pour cet exemple de conception. Il fournit également un résumé des contrôles effectués et de leurs ratios résultants, rendre les informations faciles à comprendre en un coup d'œil. Vous trouverez ci-dessous un échantillon de tableau de résumé, qui est inclus dans le rapport.

Rapport d'échantillon de skyciv
Découvrez le niveau de détail et de clarté que vous pouvez attendre d'un rapport de conception de plaque de base SkyCiv. Le rapport comprend toutes les vérifications de conception clés, équations, et les résultats présentés dans un format clair et facile à lire. Il est entièrement conforme aux normes de conception. Cliquez ci-dessous pour voir un exemple de rapport généré à l'aide du calculateur de plaque de base SkyCiv.
Logiciel d'achat de plaques de base
Achetez la version complète du module de conception de la plaque de base seul sans aucun autre module Skyviv. Cela vous donne un ensemble complet de résultats pour la conception de la plaque de base, y compris des rapports détaillés et plus de fonctionnalités.


