Exemple de conception de plaque de base en utilisant EN 1993-1-8-2005, EN 1993-1-1-2005 et EN 1992-1-1-2004
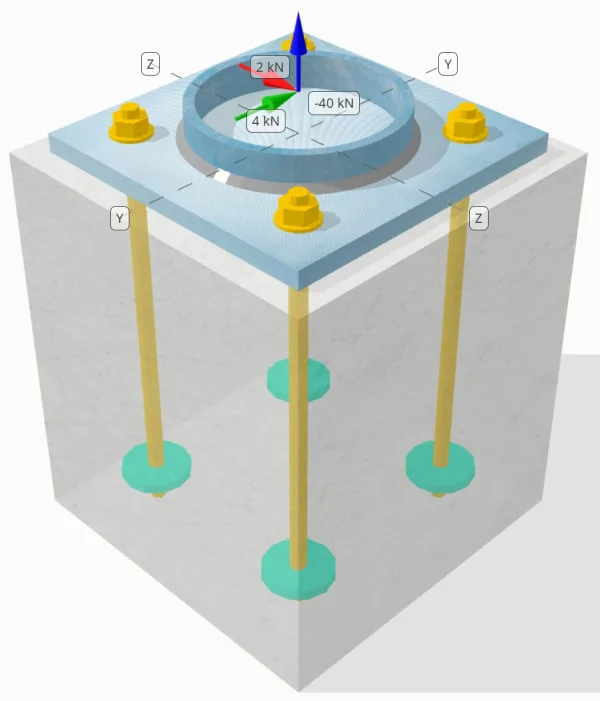
Déclaration de problème
Déterminez si la connexion de colonne à base de colonne conçue est suffisante pour un 50-kN charge de traction, 4-kN Vy charge de cisaillement, et 2-kN Vz charge de cisaillement.
Données données
Colonne:
Section colonne: CHS193.7×10
Zone de colonne: 5770.0 mm²
Matériau de colonne: S460
Plaque de base:
Dimensions de la plaque de base: 300mm x 300 mm
Épaisseur de plaque de base: 18mm
Matériau de plaque de base: S235
Jointoyer:
Épaisseur de coulis: 0 mm
Béton:
Dimensions du béton: 350mm x 350 mm
Épaisseur de béton: 400 mm
Matériau en béton: C35/45
Craquelé ou sans crates: Fissuré
Ancres:
Diamètre d'ancrage: 16 mm
Durée d'admission efficace: 350 mm
Diamètre de la plaque intégrée: 70 mm
Épaisseur de plaque intégrée: 10 mm
Matériau d'ancrage: 4.8
Soudures:
Type de soudure: Filet
Taille de soudure: 7mm
Classification du métal de remplissage: E42
Ancrer les données (de Calculateur de skyciv):
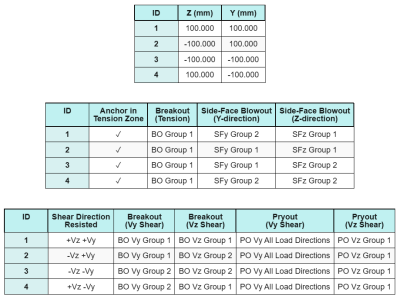
Modèle dans l'outil gratuit SkyCiv
Modélisez la conception de la plaque de base ci-dessus à l'aide de notre outil en ligne gratuit dès aujourd'hui.! Aucune inscription requise.
Remarques
Le but de cet exemple de conception est de démontrer les calculs étape par étape pour les contrôles de capacité impliquant des charges de cisaillement et axiales simultanées.. Certaines des vérifications requises ont déjà été abordées dans les exemples de conception précédents.. Veuillez vous référer aux liens fournis dans chaque section.
Calculs étape par étape
Vérifier #1: Calculer la capacité de soudure
Le plein charge de traction est résisté par le section de soudure entière, tandis que le composants de charge de cisaillement sont répartis uniquement sur une partie de la longueur totale de la soudure. Cette portion est déterminée en projetant un 90° secteur du centre de la colonne à sa circonférence. Par conséquent, seul la moitié de la circonférence totale est conçu pour résister à la charge de cisaillement.
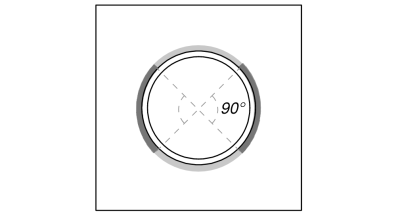
Nous calculons d'abord le Longueur totale de soudure et la partie de la soudure dans la projection de 90°.
\(L_{souder,complet} = pi d_{col} = pi fois 193.7\ \texte{mm} = 608.53\ \texte{mm}\)
\(L_{souder} = frac{\pi d_{col}}{2} = frac{\Pi Times 193.7\ \texte{mm}}{2} = 304.26\ \texte{mm}\)
Prochain, on calcule le charge de cisaillement résultante.
\(V_r = sqrt{(V_y)^ 2 + (V_z)^ 2} = sqrt{(4\ \texte{kN})^ 2 + (2\ \texte{kN})^ 2} = 4.4721\ \texte{kN}\)
Nous calculons ensuite le Ordinaire et contraintes de cisaillement, en tenant compte de la répartition de charge supposée.
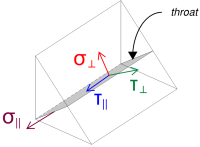
\( \sigma_{\perp} = frac{N_x}{L_{souder,complet}\,a,sqrt{2}} = frac{40\ \texte{kN}}{608.53\ \texte{mm} \fois 4.95\ \texte{mm} \fois sqrt{2}} = 9.39\ \texte{MPa} \)
\( \votre_{\perp} = frac{N_x}{L_{souder,complet}\,a,sqrt{2}} = frac{40\ \texte{kN}}{608.53\ \texte{mm} \fois 4.95\ \texte{mm} \fois sqrt{2}} = 9.39\ \texte{MPa} \)
\( \votre_{\parallèle} = frac{V_r}{L_{souder}\,a} = frac{4.4721\ \texte{kN}}{304.26\ \texte{mm} \fois 4.95\ \texte{mm}} = 2.9693\ \texte{MPa} \)
Après ça, on calcule le contraintes combinées utilisant EN 1993-1-8:2005 Eq. (4.1).
\(F_{w,Ed1} = sqrt{(\sigma_{\perp})^ 2 + 3\grand((\votre_{\perp})^ 2 + (\votre_{\parallèle})^2grand)}\)
\(F_{w,Ed1} = sqrt{(9.39\ \texte{MPa})^ 2 + 3\grand((9.39\ \texte{MPa})^ 2 + (2.9693\ \texte{MPa})^2grand)}\)
\(F_{w,Ed1} = 19.471\ \texte{MPa}\)
En même temps, Nous déterminons le contrainte sur le métal de base en utilisant la même équation.
\(F_{w,Éd2} = sigma_{\perp} = 9.39\ \texte{MPa}\)
Prochain, on calcule le capacité de soudure. Nous déterminons d'abord le résistance à la traction ultime (Facteur de service humide selon NDS) de la matériau plus faible, puis utilisez EN 1993-1-8:2005 Eq. (4.1) pour obtenir le résistance des soudures d'angle et résistance des métaux communs.
\(f_u = min!\la gauche(F_{u,\texte{col}},\ F_{u,\texte{pb}},\ F_{u,w}\droite) = min!\la gauche(550\ \texte{MPa},\ 360\ \texte{MPa},\ 500\ \texte{MPa}\droite) = 360\ \texte{MPa}\)
\(F_{w,Rd1} = frac{f_u}{\beta_w\,(\gamma_{M2,\text{souder}})} = frac{360\ \texte{MPa}}{0.8 \fois (1.25)} = 360\ \texte{MPa}\)
\(F_{w,Rd2} = frac{0.9\,f_u}{\gamma_{M2,\text{souder}}} = frac{0.9 \fois 360\ \texte{MPa}}{1.25} = 259.2\ \texte{MPa}\)
Puisque 19.471 MPa < 360 MPa, La capacité de soudure est suffisant.
Vérifier #2: Calculer la capacité de rendement en flexion de la plaque de base due à la charge de tension
Un exemple de conception pour la capacité de flexion de la plaque de base est déjà abordé dans l'exemple de conception de plaque de base pour la traction.. Veuillez vous référer à ce lien pour le calcul étape par étape.
Vérifier #3: Calculer la capacité de rupture du béton en tension
Un exemple de conception pour la capacité d'éclatement du béton en raison de la charge de traction est déjà discuté dans l'exemple de conception de plaque de base pour la traction.. Veuillez vous référer à ce lien pour le calcul étape par étape.
Vérifier #4: Calculer la capacité d'arrachement de l'ancre
Un exemple de conception pour la capacité d'arrachement de l'ancrage est déjà abordé dans l'exemple de conception de plaque de base pour la traction.. Veuillez vous référer à ce lien pour le calcul étape par étape.
Vérifier #5: Calculer la capacité d'éruption de la face latérale dans la direction en y
Un exemple de conception pour la capacité d'éclatement de la face latérale dans la direction Y est déjà abordé dans l'exemple de conception de plaque de base pour la tension.. Veuillez vous référer à ce lien pour le calcul étape par étape.
Vérifier #6: Calculer la capacité d'éruption de la face latérale dans la direction z
Un exemple de conception pour la capacité d'éclatement des faces latérales dans la direction Z est déjà abordé dans l'exemple de conception de plaque de base pour la tension.. Veuillez vous référer à ce lien pour le calcul étape par étape.
Vérifier #7: Calculer la capacité portante de la plaque de base au niveau des trous d'ancrage (Vy Shear)
Un exemple de conception pour la capacité portante de la plaque de base dans les trous d'ancrage pour le cisaillement Vy est déjà abordé dans l'exemple de conception de plaque de base pour la compression et le cisaillement.. Veuillez vous référer à ce lien pour le calcul étape par étape.
Vérifier #8: Calculer la capacité portante de la plaque de base au niveau des trous d'ancrage (Cisaillement vz)
Un exemple de conception pour la capacité portante de la plaque de base dans les trous d'ancrage pour le cisaillement Vz est déjà abordé dans l'exemple de conception de plaque de base pour la compression et le cisaillement.. Veuillez vous référer à ce lien pour le calcul étape par étape.
Vérifier #9: Calculer la capacité de rupture du béton (Vy Shear)
Un exemple de conception pour la capacité du béton en cas de rupture par éclatement due au cisaillement Vy est déjà discuté dans l'exemple de conception de plaque de base pour le cisaillement.. Veuillez vous référer à ce lien pour le calcul étape par étape.
Vérifier #10: Calculer la capacité de rupture du béton (Cisaillement vz)
Un exemple de conception pour la capacité du béton en cas de rupture par éclatement due au cisaillement Vz est déjà discuté dans l'exemple de conception de plaque de base pour le cisaillement.. Veuillez vous référer à ce lien pour le calcul étape par étape.
Vérifier #11: Calculer la capacité d'extraction
Un exemple de conception pour la capacité d'extraction du béton est déjà abordé dans l'exemple de conception de plaque de base pour le cisaillement.. Veuillez vous référer à ce lien pour le calcul étape par étape.
Vérifier #12: Calculer la capacité de cisaillement de la tige d'ancrage
L'effet du charge de traction sur la capacité de la tige d'ancrage est prise en compte dans ce contrôle si le la force de cisaillement agit avec un bras de levier. Par contre, dans cet exemple, la cisaille agit sans bras de levier. Par conséquent, l'interaction entre les contraintes de cisaillement et de traction sur la tige d'ancrage sera évaluée séparément dans le vérification des interactions.
Pour le calcul étape par étape de la capacité de cisaillement sans bras de levier, veuillez vous référer à ce lien.
Le logiciel SkyCiv Base Plate Design peut effectuer toutes les vérifications nécessaires pour déterminer si la charge de cisaillement agit avec ou sans bras de levier. Tu peux essayez l'outil gratuit aujourd'hui.
Vérifier #13: Calculer la vérification de l'interaction entre l'acier et l'ancrage
Nous utilisons EN 1992-4:2018 Le tableau 7.3 Eq. (7.54) pour évaluer le interaction entre les contraintes de cisaillement et de traction sur la tige d'ancrage. En substituant la contrainte de traction et la capacité ainsi que la contrainte de cisaillement et la capacité dans l'équation, le résultat valeur d'interaction est:
\(JE_{int} = gauche(\frac{N_{Ed}}{N_{Rd,s}}\droite)^ 2 + \la gauche(\frac{V_{Ed}}{V_{Rd,s}}\droite)^2)
\(JE_{int} = gauche(\frac{10\ \texte{kN}}{49.22\ \texte{kN}}\droite)^ 2 + \la gauche(\frac{1.118\ \texte{kN}}{38.604\ \texte{kN}}\droite)À partir de l'élévation du sol générée à partir des élévations Google 0.042117\)
Puisque 0.042 < 1.0, la vérification de l'interaction de la rupture de l'acier de la tige d'ancrage est suffisant.
Vérifier #14: Calculer le contrôle d'interaction de rupture du béton
SkyCiv automatise également les calculs de charge de neige au sol avec quelques paramètres vérification des interactions est requis pour échecs concrets sous chargement simultané de cisaillement et de traction. Pour ça, nous utilisons EN 1992-4:2018 Le tableau 7.3 Eq. (7.55) et Eq. (7.56).
Voici les ratios résultants pour tous contrôles de traction.
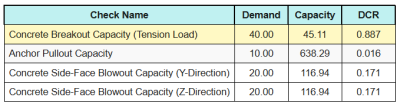
Voici les ratios résultants pour tous contrôles de cisaillement.
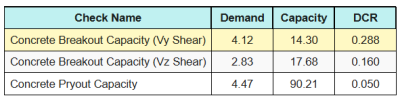
Première, nous vérifions en utilisant Eq. (7.55) et comparer le résultat à limite maximale d'interaction de 1.0.
\(JE_{\texte{cas1}} = gauche(\la gauche(\frac{N_{Ed}}{N_{Rd}}\droite)^{1.5}\droite) + \la gauche(\la gauche(\frac{V_{Ed}}{V_{Rd}}\droite)^{1.5}\droite)\)
\(JE_{\texte{cas1}} = gauche(\la gauche(\frac{40}{45.106}\droite)^{1.5}\droite) + \la gauche(\la gauche(\frac{4.1231}{14.296}\droite)^{1.5}\droite) = 0.99\)
Prochain, nous vérifions en utilisant Eq. (7.56) et comparer le résultat à limite maximale d'interaction de 1.2.
\(JE_{\texte{cas2}} = frac{N_{Ed}}{N_{Rd}} + \frac{V_{Ed}}{V_{Rd}} = frac{40}{45.106} + \frac{4.1231}{14.296} = 1.1752\)
Puisque 0.99 < 1.0 et 1.175 < 1.2, l' vérification de l'interaction des ruptures du béton est suffisant.
Résumé de la conception
Ce logiciel Logiciel de conception de plaques de base Skyciv peut générer automatiquement un rapport de calcul étape par étape pour cet exemple de conception. Il fournit également un résumé des contrôles effectués et de leurs ratios résultants, rendre les informations faciles à comprendre en un coup d'œil. Vous trouverez ci-dessous un échantillon de tableau de résumé, qui est inclus dans le rapport.
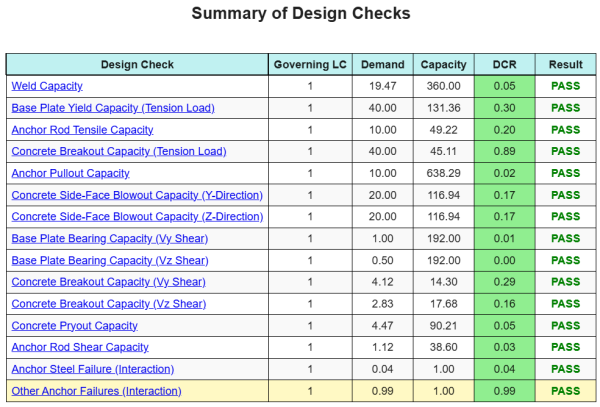
Rapport d'échantillon de skyciv
Découvrez le niveau de détail et de clarté que vous pouvez attendre d'un rapport de conception de plaque de base SkyCiv. Le rapport comprend toutes les vérifications de conception clés, équations, et les résultats présentés dans un format clair et facile à lire. Il est entièrement conforme aux normes de conception. Cliquez ci-dessous pour voir un exemple de rapport généré à l'aide du calculateur de plaque de base SkyCiv.
(Un exemple de rapport sera bientôt ajouté)
Logiciel d'achat de plaques de base
Achetez la version complète du module de conception de la plaque de base seul sans aucun autre module Skyviv. Cela vous donne un ensemble complet de résultats pour la conception de la plaque de base, y compris des rapports détaillés et plus de fonctionnalités.


