Exemple de conception de plaque de base AISC Code américain
Vous trouverez ci-dessous un exemple de calculs de plaques de base américaines couramment utilisés dans la conception de plaques de base.. Conception de la plaque de base en acier Eurocode, Conception de la plaque de base en acier Eurocode, Conception de la plaque de base en acier Eurocode:
- Conception de la plaque de base en acier Eurocode – Vous trouverez ci-dessous un exemple de calculs de plaques de base américaines couramment utilisés dans la conception de plaques de base. 318
- Conception de la plaque de base en acier Eurocode – Conception de la plaque de base en acier Eurocode, Vous trouverez ci-dessous un exemple de calculs de plaques de base américaines couramment utilisés dans la conception de plaques de base. 360
- Conception de la plaque de base en acier Eurocode – Conception de la plaque de base en acier Eurocode, Vous trouverez ci-dessous un exemple de calculs de plaques de base américaines couramment utilisés dans la conception de plaques de base.
- Conception de la plaque de base en acier Eurocode (Colonne) vérifications – Conception de la plaque de base en acier Eurocode

Actuellement, l' Conception de plaque de base en acier Conception de la plaque de base en acier Eurocode. Conception de la plaque de base en acier Eurocode, Conception de la plaque de base en acier Eurocode, afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués!
afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués:
Combinaisons de charge:
Ce logiciel Conception de plaque de base en acier Vous trouverez ci-dessous un exemple de calculs de plaques de base américaines couramment utilisés dans la conception de plaques de base. 7-10/16 Vous trouverez ci-dessous un exemple de calculs de plaques de base américaines couramment utilisés dans la conception de plaques de base.:
- \(1.4RÉ)
- \(1.2D + 1.6L + 0.5(L_{r} \texte{ ou } S texte{ ou } R)\)
- \(1.2D + 1.6(Lr texte{ ou } S texte{ ou } R) + (L texte{ ou } 0.5W)\)
- \(1.2D + 1.0W + L + 0.5(Lr texte{ ou } S texte{ ou } R)\)
- \(1.2D + 1.0E + L + 0.2S )
- \(0.9D + 1.0W)
- \(0.9D + 1.0E)
où :
\(RÉ) = charge morte
\(L) = charge vive
\(L_{r}\) = charge vive du toit
\(S ) = Charge de neige
\(R) = Charge de pluie
\(E) = tremblement de terre
\(W) = Charge de vent
afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués:
Vérification des appuis en béton ACI:
Ce logiciel Conception de plaque de base en acier Vous trouverez ci-dessous un exemple de calculs de plaques de base américaines couramment utilisés dans la conception de plaques de base. (compression) Vous trouverez ci-dessous un exemple de calculs de plaques de base américaines couramment utilisés dans la conception de plaques de base. 360-16 Eq. J8-2.
\( F_{b} = phi _{palier} \fois 0.85 \fois f'_{c} \fois A_{1} \fois sqrt{ \frac{ UNE_{2} }{ UNE_{1} } } \leq F_{b, limite} = 1.70 \fois f'_{c} \fois A_{1} \)
où:
\( F'_{c} \) Vous trouverez ci-dessous un exemple de calculs de plaques de base américaines couramment utilisés dans la conception de plaques de base.
\( UNE_{1} \) – surface de la plaque de base en contact avec la surface en béton
\( UNE_{2} \) – surface d'appui en béton
\( \phi_{palier} \) – facteur de résistance pour le béton ( valeur par défaut = 0.65 )
afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués:
Vérification de la conception des soudures AISC:
Ce logiciel Conception de plaque de base en acier Vous trouverez ci-dessous un exemple de calculs de plaques de base américaines couramment utilisés dans la conception de plaques de base. 360-16 J2
\( (je) R_{n} = R_{nul} + R_{nwt} \)
ou
\( (ii) R_{n} = 0.85R_{nul} + 1.5R_{nwt} \)
où:
\(R_{nul} \) = résistance nominale totale des soudures d'angle chargées longitudinalement.
\(R_{nwt} \) = résistance nominale totale des soudures d'angle chargées transversalement.
afin que les ingénieurs puissent revoir exactement comment ces calculs sont effectués:
Vérification de la conception des ancres ACI:
Ce logiciel Conception de plaque de base en acier Vous trouverez ci-dessous un exemple de calculs de plaques de base américaines couramment utilisés dans la conception de plaques de base. 318-19 sous le chapitre 17.
Les tiges d'ancrage sont conçues selon AISC 360-16 – J9 et ACI 318-19 – Chapitre 17. Les résistances suivantes des boulons d'ancrage sont évaluées:
- Résistance de l'acier de l'ancre en traction et en cisaillement, \( \phi N_{à} \) et \( \phi V_{à} \).
- Résistance à l'arrachement du béton en traction et cisaillement, \( \phi N_{cbg} \) et \( \phi V_{cbg} \).
- Résistance à l'arrachement du béton, \( \phi N_{p} \).
- Résistance à l'éclatement de la face latérale du béton, \( \phi N_{qn} \).
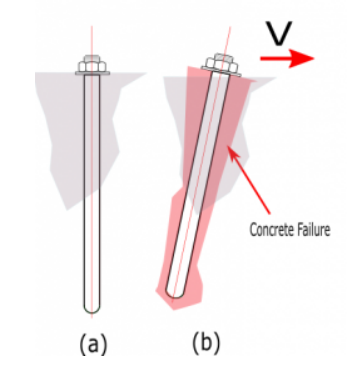
- Résistance au soulèvement du béton de l'ancrage en cisaillement, \( \phi V_{cp} \).
Résistance de l'acier de l'ancre en traction et en cisaillement

Figure A. (a) boulon incassable (b) rupture de boulon due à une rupture de tension (c) éclatement du boulon en raison d'une rupture par cisaillement
La résistance de l'acier pondérée de l'ancrage en traction et en cisaillement est déterminée selon l'ACI 318-19 – 17.6.1.2 et 17.7.1 comme
Pour la tension
\( \phi _{tension, anc} N_{à} = phi _{tension, anc} UNE_{je connais,N}F_{uta} \flèche droite \) équation 17.6.1.2
Pour cisaillement
\( \phi _{de cisaillement, anc} V_{à} = phi _{de cisaillement, anc} 0.6UNE_{je connais,V}F_{uta} \flèche droite \) équation 17.7.1.2b
où:
- \( \phi _{tension, anc} \) – facteur de réduction de résistance pour les ancrages en traction ( valeur par défaut = 0.75 )
- \( \phi _{de cisaillement, anc}\) – facteur de réduction de résistance pour les ancrages en cisaillement ( valeur par défaut = 0.65 )
- \( UNE_{je connais,N}\) – est la section efficace d'une ancre en traction.
- \( UNE_{je connais,V}\) – est la section efficace d'une ancre en cisaillement.
- \( F_{uta}\) Vous trouverez ci-dessous un exemple de calculs de plaques de base américaines couramment utilisés dans la conception de plaques de base. \(1.9F_{Oui}\) et 125 KSI (861.845 MPa)
Résistance à l'arrachement du béton

Figure B. (a) Support de boulon au béton (b) rupture du béton due à la force de traction (c) rupture du béton due à l'effort tranchant
La résistance à l'arrachement du béton pondérée de l'ancrage en traction et en cisaillement est déterminée selon l'ACI 318-19 – 17.6.2 et 17.7.1 comme
\( \phi N_{cbg} = phi frac{ UNE_{NC} }{ UNE_{Rappelles toi} } \psi_{ce,N} \psi_{ed,N} \psi_{c,N} \psi_{cp,N} N_{b} \flèche droite \) équation 17.6.2.ab
où:
\( \phi \) – facteur de réduction de la résistance des ancrages en traction ( valeur par défaut = 0.75 ).
\( UNE_{NC} \) – rupture de béton projetée d'un ancrage unique ou d'un groupe d'ancrages.
\( UNE_{Rappelles toi} \)- projeter la zone de rupture du béton d'une seule ancre, pour le calcul de la résistance à la traction si elle n'est pas limitée par la distance aux bords ou l'espacement.
\( \psi_{ce,N} \) – Facteur d’excentricité de rupture en tension.
\( \psi _{ce,N} = frac{1.00}{ 1 + \frac{e^{«}_{N}}{1.5 h_{ef}} } \leq 1.00 \flèche droite \) équation 17.6.2.3.1
\( \psi_{ed,N} \) – Facteur d’effet de cassure en tension.
(a) \( \texte{si } C_{a,min} \geq 1.5h_{ef} \texte{ ensuite } \psi _{ed,N} = 1.00 \) équation 17.6.2.4.1a
et
(b) \( \texte{si } C_{a,min} < 1.5h_{ef} \texte{ ensuite } \psi _{ed,N} = 0.70 + 0.3\frac{C_{a,min}}{1.5h_{ef}} \) équation 17.6.2.4.1b
\( \psi_{c,N} \) – Facteur de fissuration en traction.
\( \psi _{c,N} = 1.25 \) pour ancres coulées
\( \psi_{cp,N} \) – Facteur de rupture de rupture en tension.
(a) \( \texte{si } C_{a,min} \geq C_{ca} \texte{ ensuite } \psi _{cp,N} = 1.00 \) équation 17.6.2.4.1a
et
(b) \( \texte{si } C_{a,min} < C_{ca} \texte{ ensuite } \psi _{cp,N} = frac{ C_{a,min} }{ C_{ca}} \geq frac{ 1.5h_{ef} }{ C_{ca} } \) équation 17.6.2.4.1b
\( N_{b} \) – résistance de base à la rupture du béton en traction d'un seul ancrage dans le béton fissuré.
Résistance à l'arrachement du béton

Figure C. (a) Support de boulon au béton (b) arrachement du boulon du béton dû à la force de traction
La résistance à l'arrachement du béton pondérée d'une ancre est définie dans l'ACI 318-19 – 17.6.3 comme
Npn = φΨc,P Np
où:
\( \phi \) – facteur de réduction de la résistance des ancrages en traction ( valeur par défaut = 0.70 ).
\( \psi _{c, P} \) – facteur de modification pour l'état du béton
Pour béton fissuré:
\( \psi _{c, P} \) = 1.0
Pour béton non fissuré:
\( \psi _{c, P} \) = 1.4
\( N_{p} \) – Force d'arrachement de l'ancre
Pour béton fissuré:
\( N_{p} = 8A_{brg}f^{«}_{c}\) équation 17.6.3.2.2a
Pour béton non fissuré:
\( N_{p} = 0.9f^{«}_{c}e_{h}ré_{a} \flèche droite \) équation 17.6.2.2.b
où \( 3ré_{a} \leq e_{h} \leq 4.5d_{a} \)
\( f^{«}_{c} \) – résistance à la compression spécifiée du béton.
\( UNE_{brg} \) – surface d'appui nette de la tête du goujon, boulon d'ancrage ou barre déformée à tête.
\( e_{h} \) – distance entre la surface intérieure de la tige d'un boulon en J ou d'un boulon en L et l'extrémité extérieure du J- ou boulon en L.
\( ré_{a} \) – diamètre extérieur de l'ancrage ou diamètre de la tige du goujon à tête, boulon à tête, ou boulon à crochet.
Résistance à l'éclatement de la face latérale du béton

Figure D. (a) Support de boulon au béton (b) boulon présentant une rupture de béton (coup de côté) près du bord à la force de traction
La résistance pondérée à l'éclatement de la face latérale du béton d'un ancrage est définie dans l'ACI 318-19 – 17.6.4 comme
\( \phi N_{qn} = 160C_{a1}\sqrt{UNE_{brg}}\lambda _{a} \sqrt{f^{«}_{c} } \flèche droite \) équation 17.6.4.1
où:
\( f^{«}_{c} \) – résistance à la compression spécifiée du béton.
\( UNE_{brg} \) – surface d'appui nette de la tête du goujon, boulon d'ancrage ou barre déformée à tête.
\( \lambda_{a} \) – facteur de modification pour refléter les propriétés mécaniques réduites du béton léger dans certaines applications d'ancrage en béton.
Force de levier du béton de l'ancre