Conception à un seul pieu selon ACI 318 (2014)
Les pieux sont des éléments longs et minces qui transfèrent les charges de la superstructure vers un sol plus profond ou sur un rocher avec une capacité portante adéquate. Les matériaux utilisés pour les pieux peuvent inclure du bois, acier, et béton. L'installation du pieu dans le sol peut être enfoncée, percé, ou vérins qui sont ensuite connectés aux chapeaux de pieux. De nombreux facteurs, comme les conditions du site, le type de sol, la transmission de charges, sont considérés pour classer le type et l'installation des pieux. Cet article se concentrera sur la conception d'un pieu en béton conformément à l'American Concrete Institute (ACI) 318 – 2014.
Le module SkyCiv Foundation Design comprend la conception de pieux conformément à l'American Concrete Institute (ACI 318) et normes australiennes (AS 2159 & 3600).
Vous voulez essayer le logiciel Foundation Design de SkyCiv? Notre outil gratuit permet aux utilisateurs d'effectuer des calculs de charge sans aucun téléchargement ni installation!
Capacité de charge d'une pile
En général, les charges verticales appliquées sur les pieux sont portées par le palier d'extrémité du pieu, et la résistance au frottement cutané s'est développée sur toute sa longueur. La capacité de charge ultime (QU) doit être représenté par l'équation (1). Un facteur de sécurité est appliqué pour calculer la capacité de charge admissible (QA).
\({Q}_{u} = {Q}_{p} + {Q}_{s}\) (1)
QU = Capacité de charge ultime
QP = Résistance du palier d'extrémité
QS = Résistance au frottement cutané
\({Q}_{A} = frac{{Q}_{U}}{FOS} \) (2)
QA = Capacité de charge admissible
FOS = facteur de sécurité
Pour un guide plus détaillé, consultez notre article sur le calcul la résistance au frottement cutané et la capacité portante en bout.
Résistance structurelle d'un seul pieu
Les pieux sont également soumis à des forces axiales, les efforts tranchants, et moment de flexion, c'est pourquoi ils sont structurellement conçus de manière similaire aux colonnes. Section 10.5.1.1 stipule que toute charge pondérée ne doit pas dépasser ses résistances de conception correspondantes.
\( {øP}_{N} ≤ {P}_{U} \) (3a)
\( {douloureux}_{N} ≤ {M}_{U} \) (3b)
\( {øV}_{N} ≤ {V}_{U} \) (3c)
PU, MU, VU = Axial pondéré, moments de flexion, charges de cisaillement
PN, MN, VN = Axial nominal, moments de flexion, charges de cisaillement
ø = facteurs de réduction de la résistance (Le tableau 1)
| Facteurs de réduction de la force(ϕ) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Axial | 0.65-0.90 | ||||||||||||
| Flexural | 0.65-0.90 | ||||||||||||
| Tondre | 0.75 | ||||||||||||
Le tableau 1: Facteurs de réduction de la force (Le tableau 21.2.1, ACI 318-14)
Capacité de cisaillement d'un seul pieu (øVN)
La résistance nominale au cisaillement doit être équivalente aux contributions combinées des capacités de cisaillement des armatures en béton et en acier..
Résistance au cisaillement du béton (Vc)
La contribution du béton à la capacité de cisaillement est calculée comme indiqué sur l'équation (4) qui est défini sur la section 22.5.5.1 de l'ACI 318-14.
\( {V}_{c} = 0.17 × λ × sqrt{fc »} × b × d \) (4)
λ = Facteur de modification du béton = 1 (Béton de poids normal, Le tableau 19.2.4.2)
fc’ = Résistance du béton
b = largeur ou diamètre de la pile
d = 0.80 × profondeur de pile (Section 22.5.2.2)
Résistance au cisaillement des barres d'acier (Vs)
La contribution de l'armature de cisaillement latéral à la capacité de cisaillement est calculée comme le minimum entre les équations (5) et (6).
\( {V}_{s} = 0.066 × sqrt{fc »} × b × d \) (5)
\( {V}_{s} = frac{{A}_{v} × {F}_{yt} × d }{s} \) (6)
AV = Aire des armatures de cisaillement
Fyt = Limite d'élasticité des barres d'armature de cisaillement
s = espacement centre à centre des armatures de cisaillement
Résistance nominale au cisaillement (øVN)
Résumer la sortie de l'équation 4-6 doit résulter de la résistance nominale au cisaillement du pieu. Facteur de réduction de la force (ø) doit être égal à 0.75 tel que défini dans le tableau 22.2.1 de l'ACI 318-14.
\( {øV}_{N} = ø × ({V}_{c} + {V}_{s}) ≤ {øV}_{U} \) (7)
Capacités axiales et flexibles d'un seul pieu (øPN, douloureuxN )
Les capacités axiales et en flexion sont vérifiées à l'aide d'un diagramme d'interaction. Ce diagramme est une représentation visuelle du comportement des capacités de flexion et axiales provoquées par une augmentation de la charge à partir du point de flexion pur jusqu'à ce qu'un point d'équilibre soit atteint.
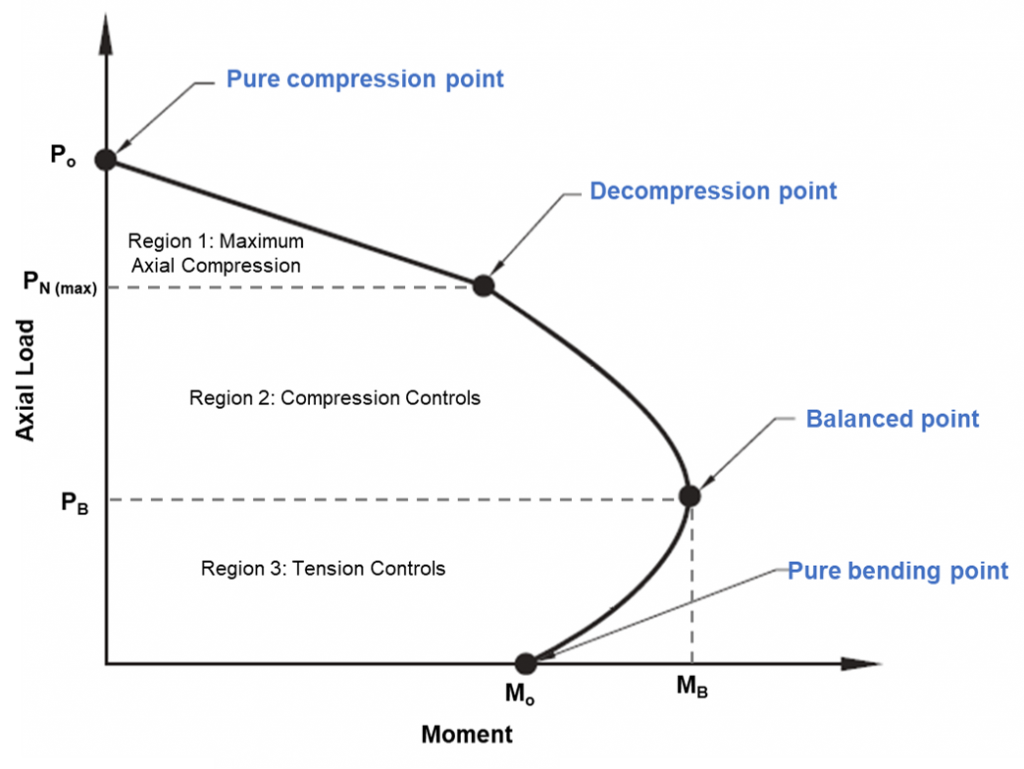
Figure 1: Diagramme d'interaction de colonne
Diagramme d'interaction de colonne
Le point de compression pure sur le diagramme est l'endroit où le pieu échouera à la compression purement. À ce point, la charge axiale est appliquée au centre de gravité plastique de la section pour rester en compression sans se plier. La résistance du pieu entre le point de compression pur et jusqu'à ce que les points de décompression puissent être calculés par interpolation linéaire. Le point de décompression est l'endroit où la déformation du béton au niveau de la fibre de compression extrême est égale à 0.003, et la déformation dans la fibre de traction extrême est nulle. Le point de flexion pur est l'endroit où la capacité de charge axiale est nulle. Entre la transition du point de décompression au point de flexion pur, une condition équilibrée est atteinte. À ce point, la déformation du béton est à sa limite (ec= 0,003), et la déformation extérieure de l'acier atteint le rendement (es= 0,0025). Toute combinaison de charge axiale et de moment de flexion en dehors du diagramme entraînera une défaillance.
Résistance à la compression axiale nominale maximale pour la conception (øPN)
La résistance axiale de calcul d'une section ne doit être limitée qu'à 80-85% de la résistance axiale nominale pour tenir compte de l'excentricité accidentelle.
\( {øP}_{N} = ø × {P}_{le} \) (8a)
\( {P}_{le} = F × [0.85 × {F}_{c} × ({A}_{g} – {A}_{st}) + ({F}_{Y} × {A}_{st}) ] \) (8b)
F = 0.80 (Liens)
F = 0.85 (Spirale)
Ag = Superficie brute de la section transversale du pieu
Ast = Surface totale des barres d'acier longitudinales
FY = Limite d'élasticité des barres d'acier
Résistance nominale à la flexion (douloureuxN)
La construction du diagramme d'interaction pour la colonne consiste à tracer une série de valeurs de PN et MN. Valeurs pour PN doit être équivalent à la somme des forces de traction et de compression, comme le montrent les figures 2a et 2b, tandis que le M correspondantN est calculé en résolvant ces forces autour de l'axe neutre. Ces forces comprennent la force de compression agissant sur la zone de compression et les forces exercées par chacune des barres d'armature qui pourraient être soit de compression, soit de traction.. Une procédure générale est suggérée ci-dessous pour construire un diagramme d'interaction en utilisant les équations présentées.
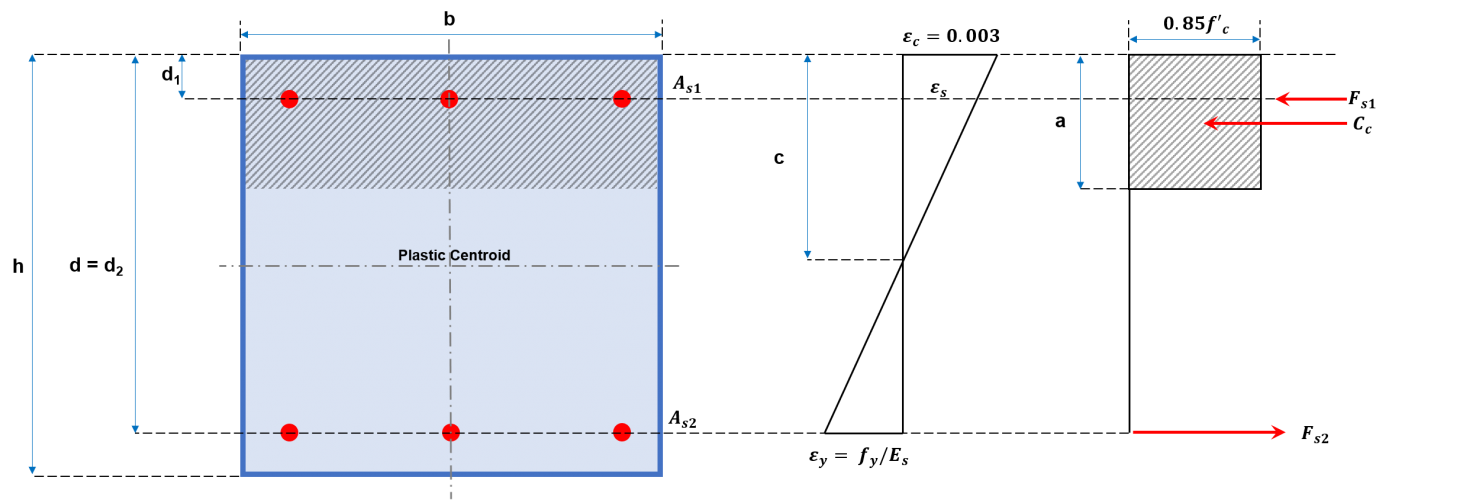
Figure 2a: Coupe transversale de poteau rectangulaire
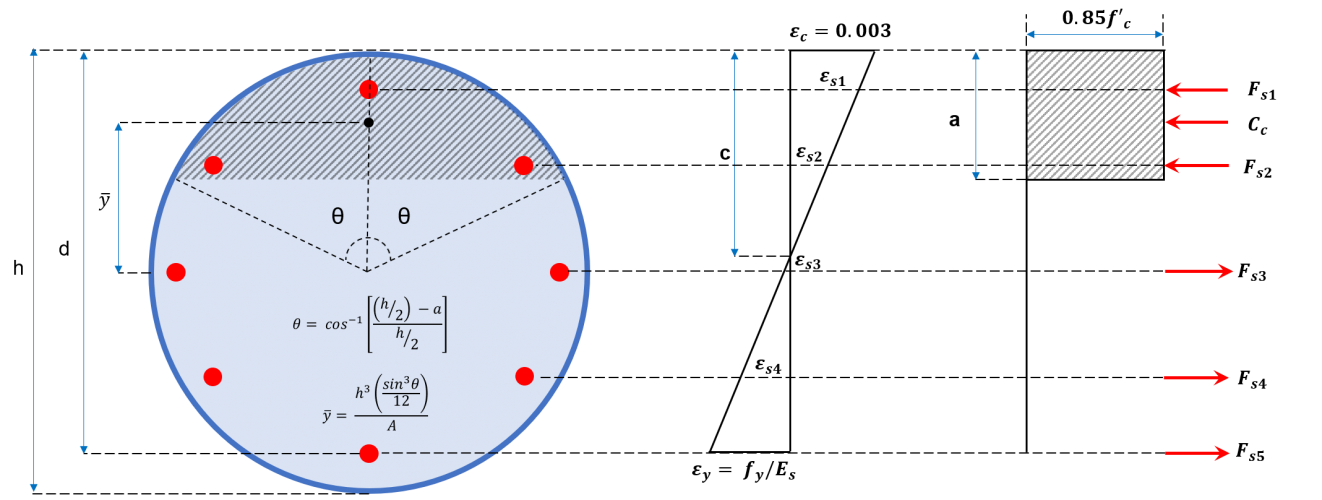
Figure 2b: Coupe transversale de poteau circulaire
Procédure générale pour le diagramme d'interaction d'une colonne
(1) Calculer la valeur de Ple et PN (équations 8a et 8b).
(2) Déterminer c et les déformations dans les renforts.
\( c = 0.003 × frac{{d}_{1}}{0.003 + (Z + {e}_{Y})} \) (9)
c = profondeur de l'axe neutre
eY = Déformation de l'acier = fY/Es
Z = valeur arbitraire (0, -0.5, -1.0, -2.5)
Une série de cas doit être considérée en sélectionnant divers emplacements de l'axe neutre, c. Pour définir les emplacements de l'axe neutre, différentes déformations de l'acier doivent être sélectionnées en multipliant une valeur arbitraire Z par la limite d'élasticité de l'acier. Il existe une large gamme de valeurs pour Z. Par contre, il n'y a que quatre points obligatoires à utiliser pour le diagramme d'interaction.
- Z = 0: À ce point, la déformation à la couche extrême en tension est nulle. Ce point marque le passage d'une épissure à recouvrement par compression autorisée sur toutes les barres longitudinales à une épissure à recouvrement de tension.
- Z = -0.5: cette distribution de déformation affecte la longueur de l'épissure à recouvrement de tension dans un poteau & est habituellement tracé sur un diagramme d'interaction.
- Z = -1: cela marque le point d'une condition équilibrée. Cette répartition des déformations marque le passage des ruptures de compression provenant de l'écrasement de la surface de compression du profilé à des ruptures de traction initiées par le rendement de l'armature longitudinale.
- Z = -2.5: ce point correspond à la limite de déformation contrôlée en tension de 0.005.
(3) Calculer les contraintes dans les couches de ferraillage.
\({F}_{et} ={e}_{et} × {E}_{s} \) (10)
Fet = Contrainte dans l'acier
eet = Déformation en acier
\({e}_{et} = frac{c -{d}_{je}}{c} × 0.003 \) (11)
Es = Module d'élasticité de l'acier
(4) Déterminer la hauteur du bloc de contrainte de compression, a.
\(a = {b}_{1} × c \) (a ≤ h)(12)
Pour f’c ≤ 4000 psi (28 MPa):
b1 = 0.85
Pour f’c > 4000 psi (28 MPa):
\( {b}_{1} = 0.85 – \frac{0.05 × (f’c – 4000)}{1000} \) (Impérial)
\( {b}_{1} = 0.85 – \frac{0.05 ×(f’c – 28)}{7} \) (Métrique)
(5) Calculer les forces dans le béton et l'acier.
Zone du bloc de contrainte de compression:
\({A}_{c} = a × b \) (Coupe transversale rectangulaire)
\({A}_{c} ={h}^{2} × frac{θ – sinθ cosθ}{4} \) (Section transversale circulaire)
Force de compression dans le béton:
\({C}_{c} = (0.85 × f’c) × {A}_{c}\) (14)
Force de traction dans l'acier (dje≤ a):
\({F}_{et} = {F}_{et} × {A}_{et} \) (15)
Force de compression dans l'acier (dje > a):
\({F}_{et} = [{F}_{et} – (0.85 × f’c)] × {A}_{et} \) (16)
(6) Calculer la capacité axiale (PN).
\({P}_{N} = {C}_{c} + Σ {F}_{et} \) (17)
(7) Calculer la capacité de flexion (MN).
\({M}_{N} = [{C}_{c} × (\frac{h}{2} – \frac{a}{2})]+ Σ [{F}_{et} × (\frac{h}{2} – {d}_{je}) \) (18)
(8) Calculer la valeur du facteur de réduction de la résistance (ø).
Comme indiqué dans le tableau 1, le facteur de réduction de la résistance à la fois axial et en flexion varie de 0.60 à 0.90. Section 21.2 de l'ACI 318-14 démontre sa valeur pour le moment, force axiale, ou moment combiné et force axiale, comme indiqué dans le tableau 2 ci-dessous.
| Classification | Spirale | Attaché |
|---|---|---|
| Compression contrôlée | 0.75 | 0.65 |
| Transition de la compression à la tension | 0.75 + [50 × (et – 0.003) ] | 0.65 + [(250/3) × (et – 0.003) ] |
| Tension contrôlée | 0.90 | 0.90 |
Le tableau 2: Facteurs de réduction de force pour Axial, moment ou combiner axial et moment (Le tableau 21.2.2, ACI 318-14)
(9) Répétez les étapes 2-8 avec différentes valeurs pour Z.
(10) Tracez dans le diagramme les valeurs de øPN et øMN.
Conception de pieux en béton avec le calculateur de fondation gratuit SkyCiv
Calculatrice de fondation gratuite SkyCiv vous aide dans la conception de pieux en béton et d'autres tâches telles que la conception de semelles et de pieux en béton. Consultez-le maintenant pour découvrir comment notre calculateur peut vous aider dans votre projet de pieux en béton!
Références
-
- Exigences du Code du Bâtiment pour le Béton Armé (2014). AC! 318-14 Institut américain du béton.
- Hsiao, J.K. (2012). Effets de l'axe de flexion sur le moment de charge (P-M) Diagrammes d'interaction pour les poteaux circulaires en béton utilisant un nombre limité d'armatures longitudinales. Journal électronique d'ingénierie structurelle 12 (1). Récupéré de http://www.ejse.org


