Estimation de la capacité des tas
L'estimation de la capacité de charge du pieu est nécessaire pour déterminer la charge axiale ultime que le pieu peut supporter. La capacité de charge ultime du pieu (Qu) équivaut à la somme de la capacité portante en bout (Qp) et résistance au frottement (Q), représenté par la figue. 1 et éq. 1. De nombreuses études et pratiques publiées déterminent la capacité portante et la résistance au frottement du pieu. Cet article se concentre sur diverses méthodes pour estimer la capacité ultime des pieux.
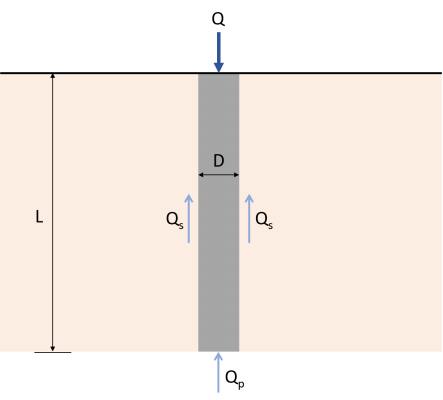
\( {Q}_{u} = {Q}_{p} + {Q}_{s} \) (1)
Qu : Capacité de charge ultime
Qp : Capacité de charge en bout
Qs : Résistance au frottement cutané
Équations universelles pour Qp et Qs
\( {Q}_{p} = {A}_{p} \fois {q}_{p} \) (2)
\( {q}_{p} = (c fois {N}_{c}) + (q’ \fois {N}_{q}) + (\gamma fois D fois {N}_{\gamma}) \) (3)
\( {Q}_{p} = {A}_{p} \fois[ (c fois {N}_{c}) + (q’ \fois {N}_{q}) ] \) (4)
La résistance de frottement totale du pieu, qui se développe sur sa longueur, peut être calculé à l'aide de cette équation:
\( {Q}_{s} = ∑ (p × ΔL × f) \) (5)
p: Périmètre de la pile
L: Longueur de pieu incrémentale sur laquelle p et f sont pris
F: Unité de résistance au frottement à n'importe quelle profondeur
Méthodes d'estimation de Qp
La méthode de Meyerhof
Sol sableux
D'après Meyerhof, la résistance ponctuelle unitaire (qp) de pieux dans le sable augmente généralement avec la longueur d'encastrement jusqu'à ce qu'elle atteigne sa valeur maximale lorsque le rapport d'encastrement (L/D) atteint une valeur critique. Taux d'enrobage critique (L/D)cr varie généralement de 16 à 18. Dans cette méthode, les pieux dans le sable sont supposés avoir une cohésion nulle (c ≈ 0), et la résistance ponctuelle unitaire ne doit pas dépasser la résistance ponctuelle limite (ql), qui est donnée par Eq. 7. Le facteur de capacité portante (Nq) les valeurs sont directement proportionnelles à l'angle de frottement du sol de la couche d'appui (Le tableau 1). Basé sur la théorie de Meyerhof, l'équation universelle pour Qp (Éq.4) peut être simplifié en:
\( {Q}_{p} = {A}_{p} \fois (q’ \fois {N}_{q}) \leq ({A}_{p} \fois {q}_{l}) \) (6)
\( {q}_{l} = 0.5 \fois {p}_{a} \fois {N}_{q} \fois bronzé (\dans les équations précédentes) \) (7)
ql : Résistance du point limite
pa: Pression atmosphérique (≈100kN/m2)
\( \[object Window]): Angle de frottement efficace du sol à la pointe du pieu
Le tableau 1: Valeurs interpolées de Nq (La théorie de Meyerhof)
Sol argileux
Équation 4 peut également calculer la capacité portante en bout de pieux dans des sols argileux ou cohésifs (φ ≈ 0). Étant donné que l'angle de frottement du sol est négligé et que le facteur de capacité portante (Nc) a une valeur constante de 9 pour les sols cohésifs, L'équation 4 peut être écrite comme:
\( {Q}_{p} = {A}_{p} \fois c fois {N}_{c} = 9 \fois c fois {A}_{p} \) (8)
Méthode de Vesic
La méthode de Vesic pour calculer la capacité portante en pointe sur les sols sableux ou argileux est basée sur sa théorie de l'expansion des cavités.
Sol sableux
Basé sur sa théorie, la capacité portante des pieux dans le sable peut être estimée à l'aide des équations suivantes:
\( {Q}_{p} = {A}_{p} \fois barre{\sigma'}_{le} \fois {N}_{\sigma} \) (9)
\(\bar{\sigma'}_{le} = frac{1 + (2 \fois {K}_{le})}{3} \fois q') (10)
\( {K}_{le} = 1 – sin \phi’\) (11)
\( {N}_{\sigma} = frac{3 \fois {N}_{q}}{1 + (2 \fois {K}_{le})} \) (12)
\(\bar{\sigma'}_{le} \) : Contrainte normale effective moyenne au sol au niveau de la pointe du pieu
Ko: Coefficient de pression des terres au repos
Nσ: Facteur de capacité portante
Sol argileux
Idem avec la méthode de Meyerhof, Eq. 4 est également applicable pour calculer la capacité portante en pointe des pieux en argile. Par contre, la valeur du facteur de capacité portante (Nc) est un facteur d'indice de rigidité (Ir). D'après sa théorie de l'expansion des cavités, Nc et moir peut être estimé par:
\( {N}_{c} = (\frac{4}{3}) \fois [ln({I}_{r}) + 1] + \frac{\pi}{2} + 1 \) (13)
\( {I}_{r} = frac{{E}_{s}}{3 \fois c} \) (Pour φ ≈ 0)(14)
Ir: Indice de rigidité
Es: Module d'élasticité du sol
Méthode de Coyle et Castello (Sol sableux)
Basé sur 24 essais de chargement à grande échelle sur le terrain de pieux battus dans le sable, Coyle et Castello ont suggéré que la capacité portante en bout des pieux peut être calculée à l'aide de l'équation 15.. Les valeurs du facteur de capacité portante (Nq) est un facteur à la fois du rapport d'enrobage (L/D) et l'angle de frottement du sol (Phi'), comme le montre la figure. 2
\( {Q}_{p} = {A}_{p} \fois (q’ \fois {N}_{q}) \) (15)
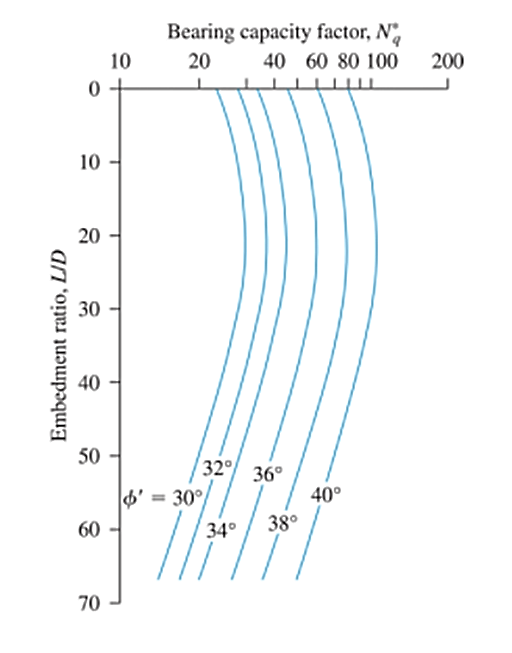
Figure 2: Variation de Nq avec L/D & la spécification fournit un traitement intégré de la conception de la résistance admissible’ (Redessiné après Coyle & Château, 1981)
Source: Le, Braja. Principes de l'ingénierie des fondations (7e édition, p.564)
Méthodes d'estimation de Qs
Résistance au frottement des pieux dans le sable
La résistance de frottement unitaire des pieux dans le sable, comme indiqué dans l'équation. 5, prend en compte plusieurs facteurs assez difficiles à calculer. Il comprend le coefficient de pression des terres (K) & angle de frottement sol-pieu, qui ont tous deux des valeurs variables en fonction de l'approche à utiliser ou des données de sol disponibles.
\( f = Kfois {\sigma}_{le}’ \fois bronzé (\delta) \) (15)
K: Coefficient de pression de terre efficace
σ’le: Contrainte verticale effective à la profondeur considérée
ré: Angle de frottement sol-pieu
Voici les différentes façons d'estimer le coefficient de pression de terre effectif et les valeurs d'angle de frottement du sol. Ces variables sont un facteur de l'angle de frottement du sol (Phi') ou type de pieu.
Coefficient de pression de terre efficace
Le sol exerce une pression de terre latérale sur la surface du pieu. Il est nécessaire de tenir compte de cette pression sur la conception ou l'analyse de la stabilité. Voici les différentes façons de déterminer les coefficients de pression des terres pour calculer la résistance de frottement unitaire des pieux dans le sable.
NAVFAC DM 7.2
| Type de pile | Compression | Soulèvement |
|---|---|---|
Le tableau 2: Coefficient de pression de terre, K (NAVFAC DM 7.2)
Moyenne K Méthode
Le coefficient de pression des terres (K) peut également être évalué en prenant la moyenne du coefficient de pression des terres au repos (K0), pression de terre active (Ka), et pression de terre passive (Kp), comme le montrent les équations 16-19.
\( K =frac{{K}_{0} + {K}_{a} + {K}_{p}}{3} \) (16)
\( (K)_{0} =1 – péché phi \) (17)
\( (K_{a} =1 – {bronzer}^{2}( \frac{45 – \phi}{2}) \) (18)
\( (K_{p} =1 + {bronzer}^{2}( \frac{45 + \phi}{2}) \) (19)
Mansur et Hunter (1970)
Basé sur différents résultats de test de charge sur le terrain, Mansur et Hunter ont conclu les valeurs du coefficient de pression des terres avec les types de pieux correspondants.
| Type de pile | K |
|---|---|
Le tableau 3: Coefficient de pression de terre, K (Mansur et Hunter, 1970)
Angle de frottement sol-pieu
L'angle de frottement entre le sol et la surface du pieu est un aspect essentiel de la conception des fondations. Pratiquement, de nombreux ingénieurs évaluent cette valeur comme étant égale à 2/3 de l'angle de frottement interne du sol. Par contre, sur la base de l'étude de Coyle et Castello dans 1981, l'angle de frottement sol-pieu est approximativement équivalent à 80% de l'angle de frottement interne du sol. En revanche, NAVFAC DM7.2 utilise ces valeurs pour estimer l'angle de frottement entre le sol et le pieu:
| Type de pile | ré |
|---|---|
Le tableau 4: Angle de frottement sol-pieu (ré) (NAVFAC DM 7.2)
Résistance au frottement des pieux en argile
Le calcul de la résistance au frottement des pieux dans les sols argileux peut être aussi difficile que celui des sols sableux en raison de l'introduction de nouvelles variables, qui ne sont pas aussi faciles à déterminer. Par contre, il existe plusieurs méthodes disponibles pour obtenir les valeurs de ces variables.
Méthode λ
Basé sur l'étude de Vijayvergiya et Focht en 1972, la résistance de frottement totale des pieux en argile peut être estimée en déterminant la résistance de frottement unitaire moyenne du pieu, comme le montrent les équations 20 et 21. Les valeurs λ changent à mesure que la profondeur de pénétration du pieu augmente. Le tableau 5 montre la variation de λ avec la longueur d'encastrement du pieu.
\( {F}_{de} = lambdafois [\bar{\sigma'}_{le} +( 2 \fois {c}_{u})] \) (20)
\({Q}_{s} = p fois L fois {F}_{de} \) (21)
\( \bar{\sigma'}_{le} \): Contrainte verticale efficace moyenne pour toute la longueur d'ancrage
cu: Résistance moyenne au cisaillement non drainé
| L (m) | λ |
|---|---|
Le tableau 5: Variation de λ avec la longueur d'encastrement du pieu (L)
Méthode α
La méthode α suggère que la résistance de frottement unitaire des pieux est équivalente au produit de la cohésion non drainée de la couche de sol et de son facteur d'adhérence empirique correspondant (une). Le tableau 6 montre la valeur correspondante du facteur d'adhérence avec le rapport de la cohésion non drainée et de la pression atmosphérique (cu/pa).
\(f = alphafois {c}_{u}\) (22)
Par conséquent, la résistance totale au frottement d'un pieu dans l'argile utilisant cette méthode peut être réécrite comme:
\({Q}_{s} = somme (f times p times Delta L) = somme (\alpha fois {c}_{u} \fois p fois Delta L)\) (23)
| cu/pa | une |
|---|---|
| 0.8 | |
pa = pression atmosphérique ≈ 100 kN / m2
Le tableau 6: variante d'un (Terzaghi, Picorer, et Mesri, 1996)
Méthode β
La pression de l'eau interstitielle autour du pieu augmente lorsque le pieu est enfoncé dans des argiles saturées. Cette méthode, basé sur une analyse efficace des contraintes, convient à long terme (drainé) analyses de la capacité de charge du pieu en tenant compte de la dissipation progressive de la pression interstitielle excessive dans le temps. D'après Tomlinson (1971), les pieux enfoncés dans des argiles molles supposent que les ruptures se produisent dans le sol remoulé près de la surface du pieu. Basé sur l'équation. 15, le terme (K × tanδ) pour la résistance de frottement unitaire des pieux dans le sable doit être représentée par β. L'angle de frottement du sol (ré) doit être remplacé par un angle de frottement drainé remoulé du sol (Phi’R). Ainsi, la résistance de frottement unitaire des pieux en argile est estimée égale à:
\(f = beta times {\sigma'}_{le}\) (24)
\(\bêta = K fois tan {\Phi'}_{R}\) (25)
De façon conservatrice, le coefficient de pression des terres (K) est équivalent au coefficient de pression des terres au repos (K0) qui varie pour les argiles normalement consolidées et les argiles surconsolidées, comme indiqué dans les équations suivantes:
\( K = {K}_{0} = 1 – sin {\Phi'}_{R}\) (Argiles normalement consolidées) (26)
\( K = {K}_{0} = (1 – sin {\Phi'}_{R}) \fois sqrt(dans les équations précédentes)\) (Argiles surconsolidées) (27)
dans les équations précédentes: Ratio de surconsolidation
Vous voulez essayer le logiciel Foundation Design de SkyCiv? Notre outil gratuit permet aux utilisateurs d'effectuer des calculs de charge sans aucun téléchargement ni installation!
Références:
- Le, B.M. (2007). Principes de l'ingénierie des fondations (7e édition). Ingénierie globale
- Rajapakse, R. (2016). Conception de pieux et règle de construction du pouce (2nd édition). Elsevier Inc.
- Tomlinson, M.J. (2004). Conception de pieux et pratique de construction (4e édition). E & FN Spon.


