Resumen
La tensión de flexión es uno de los valores más importantes en el diseño estructural., Como ocurre con la mayoría de las vigas horizontales, este suele ser un diseño crítico o rector.. Como se carga una viga horizontal, genera momento flector tensiones en las fibras superiores e inferiores de la sección que pueden sobrecargar la sección y hacer que ceda o falle por completo.
Al calcular la tensión de flexión, es importante considerar lo siguiente:
- Momento de Inercia de tu sección – Afecta directamente a la tensión de flexión.
- ¿En qué parte de la viga estás comprobando? – La tensión de flexión generalmente aumenta cuanto más se aleja del eje neutro de la sección. (de ahí que las tensiones sean mayores en la parte superior e inferior de la sección.)
- Las propiedades materiales – materiales más fuertes (mayor límite elástico, por ejemplo) Puede soportar tensiones más altas y puede ser más adecuado en ciertos diseños.
- Formas de sección transversal – como con el punto (1) encima – diferentes secciones son muy adecuadas para soportar mayores tensiones de flexión, dados sus valores más altos de momento de inercia
- Dirección del estrés – La flexión puede ocurrir tanto en el eje mayor como en el menor de una sección dependiendo de la dirección de la carga..
- A menudo, Estos esfuerzos de flexión se pueden combinar con esfuerzos cortantes o axiales. (debido a fuerzas en otras direcciones), aumentar la tensión total en una viga
En la siguiente guía exploraremos principalmente cómo calcular la tensión de flexión. (particularmente en un I Beam), pero es importante tener en cuenta el contexto anterior al aprender estos principios..
Cómo calcular el esfuerzo de flexión en vigas?
Comprender la tensión de flexión es importante porque la flexión de la viga juega un papel crucial en el diseño de vigas.. Este tutorial verá cómo calcular la tensión de flexión en una viga con una fórmula. Esta fórmula relaciona la distribución de tensiones longitudinales en una viga con la tensión interna momento flector actuando sobre la sección transversal de la viga. Suponemos que el material de la viga es lineal-elástico (Es decir. Ley de Hooke es aplicable).
1. Calcule la tensión de flexión a mano con fórmulas de tensión de flexión (Ecuaciones)
Veamos un ejemplo. Considere la viga en I que se muestra a continuación:
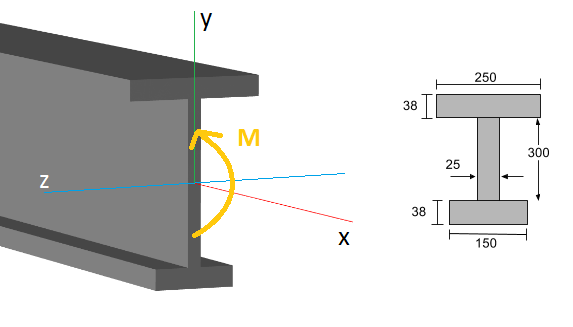
En un punto específico a lo largo de la longitud de la viga (el eje x), existe un momento flector interno (M), normalmente determinado usando un diagrama de momento de flexión. La fórmula general de la tensión de flexión. (o estrés normal) en la sección es:

Al considerar una sección específica de una viga, queda claro que la tensión de flexión alcanzará su valor máximo a una distancia específica del eje neutral (y). Así, el esfuerzo de flexión máximo ocurrirá en la parte superior o inferior de la sección de la viga, dependiendo de qué distancia es mayor:
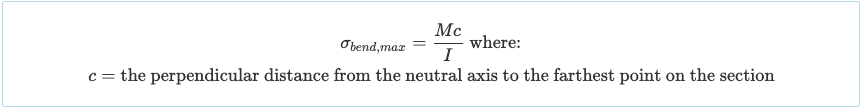
Consideremos el ejemplo real de nuestra viga en I que se muestra arriba. En nuestro anterior tutorial de momento de inercia, ya encontramos que el momento de inercia sobre el eje neutral es I = 4.74×108 mm4. Adicionalmente, en el tutorial centroide, encontramos el centroide y, por lo tanto, la ubicación del eje neutro es 216.29 mm desde la parte inferior de la sección. Esto se muestra a continuación:
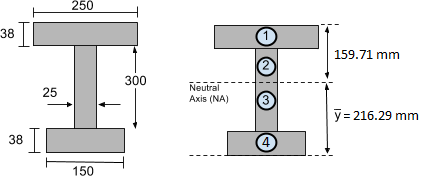
Por lo general, es necesario determinar el esfuerzo de flexión máximo experimentado por una sección. Por ejemplo, supongamos que hemos determinado, del diagrama de momento flector, que la viga encuentra un momento flector máximo de 50 kN-m o 50,000 Nm (después de convertir las unidades de momento de flexión).
Luego, debemos encontrar si la parte superior o inferior de la sección está más alejada del eje neutral.. Claramente, la parte inferior de la sección tiene una mayor distancia, midiendo c = 216.29 mm. con esta informacion, Podemos proceder a calcular la tensión máxima empleando la fórmula de tensión de flexión proporcionada anteriormente.:

De igual forma, podríamos encontrar la tensión de flexión en la parte superior de la sección, como sabemos que es y = 159.71 mm del eje neutral (EN):

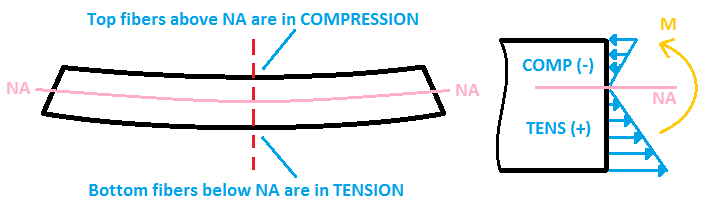
La consideración final involucra determinar si el esfuerzo de la viga está causando compresión o tensión en las fibras de la sección..
- Si la viga se hunde como un “U” forma, las fibras superiores experimentan compresión (esfuerzo negativo), mientras que las fibras inferiores sufren tensión (esfuerzo positivo).
- Si la viga se hunde al revés “U” forma, la situación es al revés: las fibras inferiores están sujetas a compresión, mientras que las fibras superiores experimentan tensión.
2. Calcule la tensión de flexión usando el software
La sección anterior ha analizado la fórmula de tensión de flexión para el cálculo manual., pero ya no tienes que hacerlo manualmente tú mismo como el Calculadora de vigas de SkyCiv puede ayudarle a encontrar la tensión cortante y de flexión en una viga con un solo clic. Simplemente modelando la viga, incorporando soportes, y aplicando cargas, puede obtener las tensiones máximas con esta calculadora de tensión de flexión. La siguiente imagen muestra un ejemplo de una viga en I que experimenta tensión de flexión:
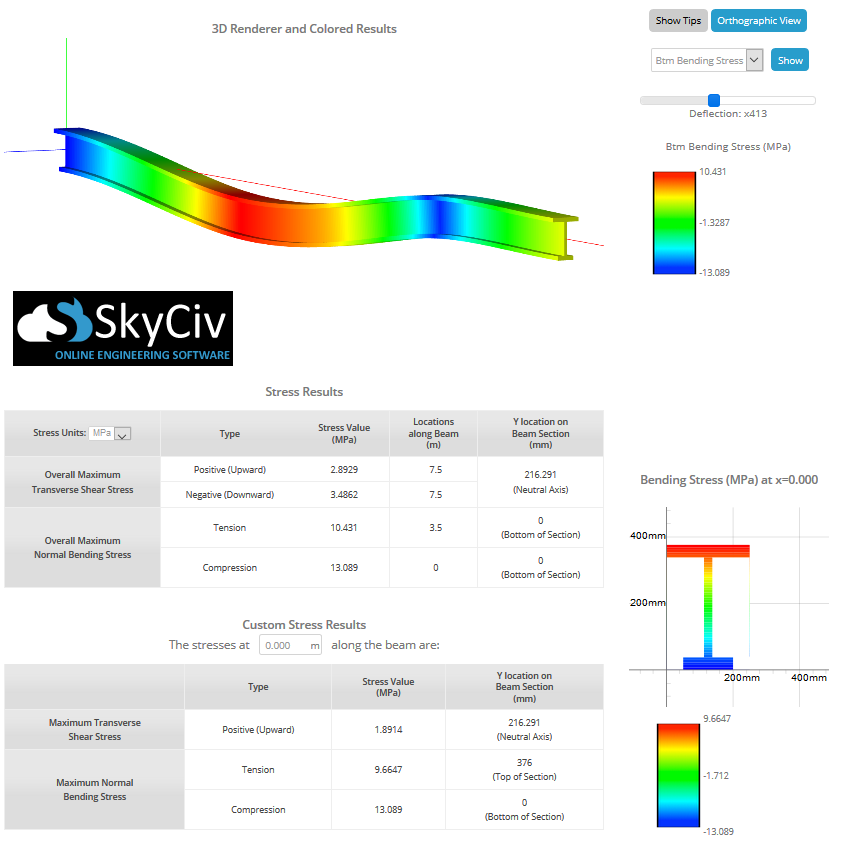
Los usuarios también pueden utilizar el siguiente Software de esfuerzo de vigas para calcular la tensión de flexión y otras tensiones de la viga, usando una herramienta simple de construcción de secciones. Así que echa un vistazo a nuestra herramienta Beam arriba o regístrate para experimentar el software gratis hoy.!
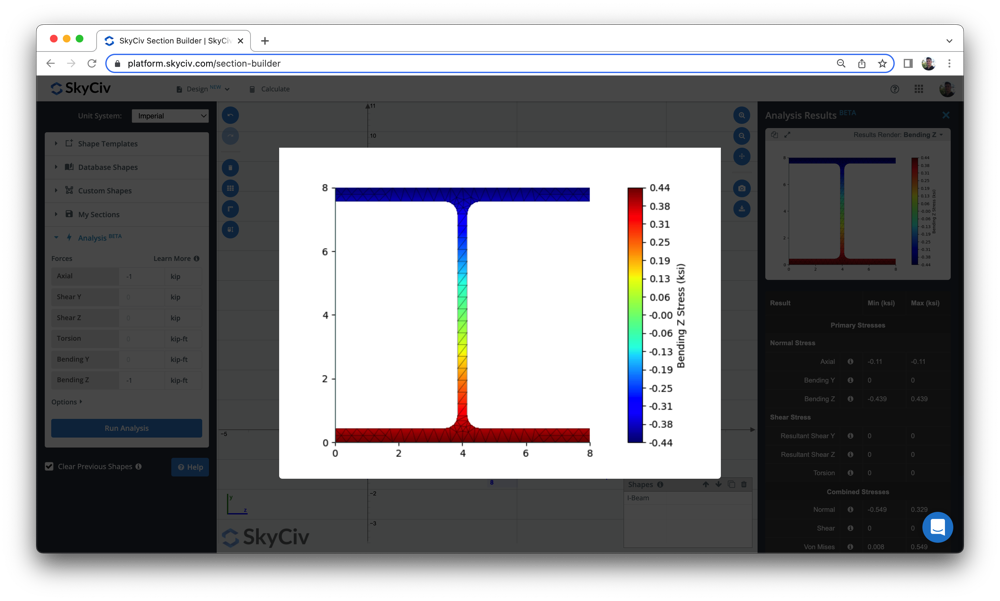
Para más documentación sobre vigas, visita nuestros artículos sobre calcular la tensión de flexión de una sección de viga, cómo encontrar el momento flector, determinar las reacciones en el soporte, y deflexión de viga.


