Cálculo de la presión lateral de la tierra en un muro de contención
Una de las principales cargas que actúan sobre un muro de contención es el empuje lateral de tierra.. Cálculo de la presión lateral de la tierra debido a las cargas de sobrecarga en el muro de contención, hacer una buena estimación de su magnitud y distribución es determinante en el diseño de un Muro de Contención de Hormigón. En general, hay tres tipos diferentes de empuje lateral de tierra dependiendo de la dirección en que el muro tiende a moverse:
- Presión de tierra en reposo: Cuando la pared está completamente restringida de moverse
- Presión de tierra activa: Cuando la pared puede inclinarse lejos del suelo retenido
- Presión pasiva de tierra: Cuando la pared puede ser empujada hacia el suelo retenido
En este artículo, nos centraremos en describir las fórmulas para cada uno de los casos de empuje de tierras mencionados anteriormente.
Distribución de presión de tierra lateral
En general, la presión lateral de la tierra se comporta igual que la presión hidrostática. Tener un valor cero en la superficie y un valor máximo en el punto más profundo siguiendo una distribución lineal entre los dos límites mencionados. Por lo tanto, la distribución de tensión horizontal del subsuelo se describe mediante la siguiente expresión:
\(\sigma_h = K_* \cdot (\gama z)\)
Dónde \(K_*\) toma el valor de \(K_o\) para el caso de presión en reposo, \(K_a\) para el caso de presión activa, y \(K_p\) para el caso de presión pasiva.
Integrando la expresión dada para la tensión subsuperficial lateral de \(0\) a \(H\) in \(desde), la resultante resulta ser:
\(P_*=\frac{1}{2} K_* \cdot \gamma \cdot H^2\)
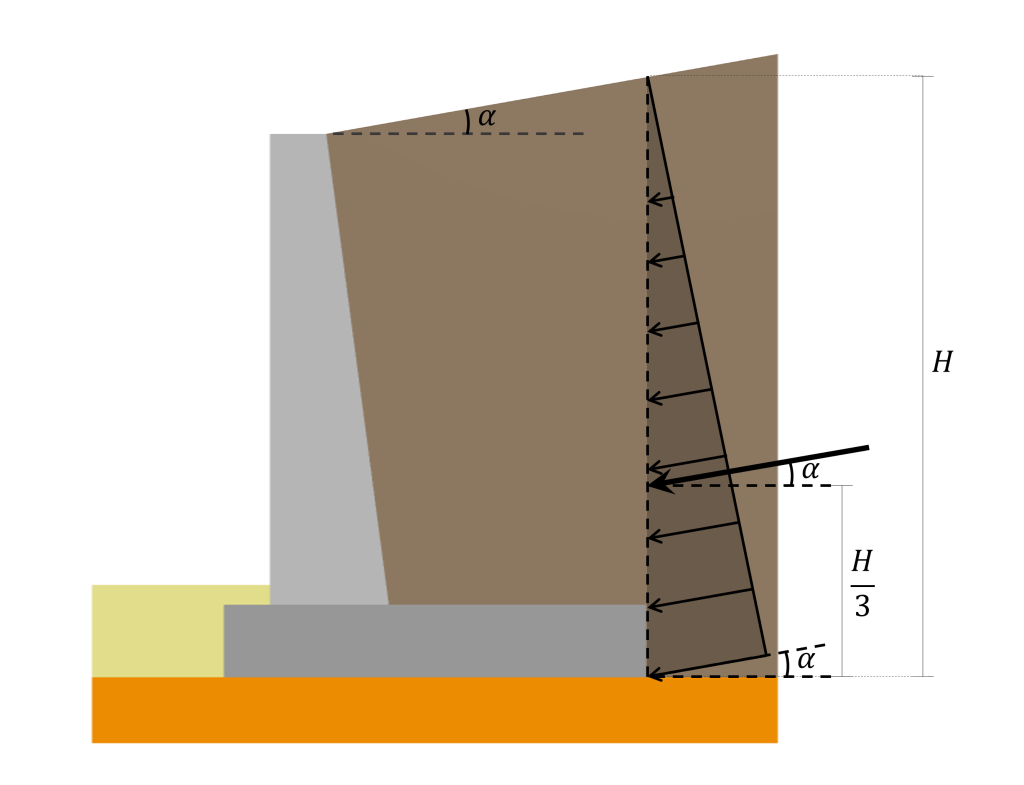
La línea de acción de esta resultante se encuentra \(\frac{2}{3}H\) de la superficie. La distribución lateral del empuje de tierra, su resultante, y la ubicación descrita anteriormente se ilustran en la siguiente imagen:
Es importante mencionar que la distribución presentada y el método de cálculo resultante solo se aplican a las presiones del suelo que actúan sobre una cara posterior vertical.. En el caso de un muro de contención con una cara posterior inclinada (como el de la imagen de arriba), la superficie donde actúa la presión del suelo se sigue considerando vertical ya que se supone que actúa en un plano vertical situado donde termina el talón.
Adicionalmente, cuando el relleno está inclinado en algún ángulo \(\alpha\) con respecto a la horizontal, la distribución de presión y su resultante están inclinadas en ese mismo ángulo \(\alpha\) como se ilustra a continuación:
Estimar correctamente la distribución de la presión lateral del suelo y su resultante es un paso crucial en el proceso de diseño de muros de contención.. y el otro de, y el otro de aquí. Profundicemos ahora en las fórmulas para calcular la presión lateral de tierra resultante ejercida sobre un muro de contención por el suelo en diferentes condiciones..
Empuje lateral de tierras en reposo
Este enfoque para calcular la presión lateral de la tierra contra un muro de contención solo se puede usar si el muro está completamente en reposo y no se le permite alejarse del suelo ni moverse hacia el suelo., esta condición asegura que la deformación horizontal en el suelo sea cero. Para este caso, el coeficiente de presión en reposo (\(K_o\)) es el que reemplaza \(K_*\) en las ecuaciones anteriores. Ese coeficiente es la única incógnita para calcular la distribución de presión y su resultante. Para suelos normalmente consolidados, la relacion para \(K_o\) es:
\(K_o = 1 pecado(\fi')\)
Dónde \(\phi’\) es el ángulo efectivo de fricción del suelo en consideración.
Para suelo sobreconsolidado, el coeficiente se puede calcular utilizando la siguiente expresión:
\(K_o = (1-sin(\fi'))\cdot OCR^{sin(\fi')}\)
Dónde \(\phi’\) es el ángulo de fricción efectivo, y \(OCR\) la relación de sobreconsolidación del suelo en consideración.
Reemplazando este coeficiente en la expresión para calcular la fuerza resultante de la presión lateral de la tierra en reposo se obtiene:
\(P_o=\frac{1}{2} \gamma \cdot H^2 \cdot K_o\)
Presión de tierra lateral activa
El enfoque anterior se puede utilizar cuando el muro no cede en absoluto., sin embargo, si una pared tiende a alejarse del suelo, la presión del suelo sobre la pared a cualquier profundidad disminuirá. Para este caso, el coeficiente de presión activa (\(K_a\)) es el que reemplaza \(K_*\) en las ecuaciones iniciales. Usando el enfoque de Rankine para un relleno granular, y suponiendo que la presión actúa en un cara posterior vertical, el coeficiente de presión activa del suelo se puede calcular utilizando la ecuación:
\(K_a=porque(\alfa) \frac{cos(\alfa) – \sqrt{porque^2(\alfa) – porque^2(\fi')}}{cos(\alfa) + \sqrt{porque^2(\alfa) – porque^2(\fi')}}\)
Dónde \(\phi’\) es el ángulo de fricción del suelo en consideración y \(\alpha\) es el ángulo de inclinación de la superficie de relleno con respecto a la horizontal.
Reemplazando este coeficiente en la expresión para calcular la fuerza resultante de la presión lateral del suelo en condiciones activas se obtiene:
\(P_a=\frac{1}{2} \gamma \cdot H^2 \cdot K_a\)
Los cálculos de presión activa de Rankine presentados anteriormente se basan en la suposición de que la pared no tiene fricción..
Empuje de tierra lateral pasivo
La presión lateral de la tierra que actúa sobre un muro de contención se considera pasiva cuando el muro se empuja hacia la masa del suelo., en esa condición, la tensión horizontal aumentará con respecto a la condición de reposo. Para este caso, el coeficiente de presión pasiva (\(K_p\)) es el que reemplaza \(K_*\) en las ecuaciones iniciales. Usando el enfoque de Rankine para un relleno granular, y suponiendo que la presión actúa en un cara posterior vertical, el coeficiente de empuje pasivo del suelo se puede calcular utilizando las expresiones:
Cuando el relleno es completamente horizontal
\(K_p = tan^2(45º+\frac{\fi'}{2})\)
Cuando el relleno está inclinado un cierto ángulo con respecto a la horizontal
\(K_p=cos(\alfa) \frac{cos(\alfa) + \sqrt{porque^2(\alfa) – porque^2(\fi')}}{cos(\alfa) – \sqrt{porque^2(\alfa) – porque^2(\fi')}}\)
Dónde \(\phi’\) es el ángulo de fricción del suelo en consideración y \(\alpha\) es el ángulo de inclinación de la superficie de relleno con respecto a la horizontal.
Reemplazando este coeficiente en la expresión para calcular la fuerza resultante de la presión lateral del suelo en condiciones pasivas se obtiene:
\(P_p=\frac{1}{2} \gamma \cdot H^2 \cdot K_p\)
De nuevo, los cálculos de presión activa de Rankine presentados anteriormente se basan en la suposición de que la pared no tiene fricción.
Referencias
Calculadora de Muros de Contención
SkyCiv ofrece una calculadora de muro de contención gratuita que calculará la presión lateral de la tierra en el muro, SkyCiv ofrece una calculadora de muro de contención gratuita que calculará la presión lateral de la tierra en el muro. La versión de pago muestra todos los cálculos, así puedes ir paso por paso, En el caso de que la zapata se extienda también alejándose del suelo retenido, deslizamiento, En el caso de que la zapata se extienda también alejándose del suelo retenido!
Desarrollador de producto
BEng (Civil)