Definición de análisis de frecuencia?
Al diseñar edificios, hay dos tipos de cargas considerar: estático y dinámico. para el primero, solo se necesita calcular la respuesta directa de la estructura frente a las cargas permanentes aplicadas en términos de desplazamiento y tensiones. Esto se puede lograr utilizando la rigidez o el método de elementos finitos.
En el caso del análisis dinámico, es más desafiante considerar el rango de posibles variaciones en la respuesta de la estructura debido a cargas dependientes del tiempo. Por lo tanto, algunas nuevas herramientas o funciones se vuelven esenciales para incluir en el análisis. Entonces, análisis de frecuencia, un método fundamental en la mecánica de vibraciones, surge.
Este método obtiene la variación en el tiempo del movimiento de la estructura debido a las cargas dinámicas aplicadas. Más específicamente, esto implica utilizar las propiedades naturales de vibración del sistema estructural para calcular las fuerzas internas, desplazamientos, problemas de estabilidad, etc..
Para más información sobre el tema, sugerimos leer un artículo de SkyCiv que explica brevemente cómo realizar un Análisis de frecuencia dinámica usando Software de Análisis Estructural SkyCiv.
¿Por qué el análisis de frecuencia es relevante para el diseño??
La mejor manera de medir la importancia del análisis de frecuencia en un diseño es observar el caso de algunas estructuras que han fallado debido a un mal comportamiento dinámico.. Un puente famoso en América del Norte es el Tacoma Narrows, que finalmente colapsó después de vibraciones periódicas sostenidas inducidas por el viento. Las siguientes imágenes mostrarán el aumento del desplazamiento a lo largo del puente justo antes del colapso., centrado principalmente en la carretera:

Figura yo. Vibraciones torsionales laterales en el puente Tacoma Narrows

Figura ii. Aumento del desplazamiento en el puente antes del colapso.

Figura III. Colapso catastrófico del puente
En este estudio de caso, no se realizó un análisis de frecuencia adecuado y la estructura no se diseñó adecuadamente para considerar la frecuencia natural de la estructura.
péndulo simple
El análisis de frecuencia estudia las diferentes formas que adopta una estructura cuando es sometida a acciones dinámicas externas. Es por eso que obtienes varios modos. Luego usando estos formularios, podemos establecer el tamaño de los elementos de la estructura a través de los esfuerzos internos necesarios para garantizar el equilibrio.
Antes de profundizar en las consideraciones técnicas y matemáticas para el análisis de frecuencia, revise el siguiente sistema simple de una columna de péndulo que se muestra en la figura iv.
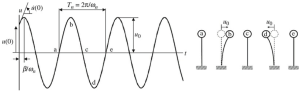
Figura IV. La respuesta dinámica de un sistema de péndulo de vibración libre
Usando un análisis simple como se indica en la última imagen., podemos definir el movimiento de la masa superior para la columna del péndulo cada vez. El objetivo principal de este artículo será cubrir el análisis de frecuencia para dos casos típicos., uno y varios grados de libertad.
Un solo grado de libertad
Este caso particular es el más simple para el análisis dinámico.. El comportamiento se describe usando la ley de equilibrio de D'Alembert, una extensión de la segunda ley de Newton.
La siguiente figura muestra los elementos del sistema SDOF, rigidez (k), mojadura (c), y fuente de masa (m) para fuerzas de inercia. La fuerza externa variable en el tiempo aplicada sobre la masa está representada por \({Precios(t)}\).
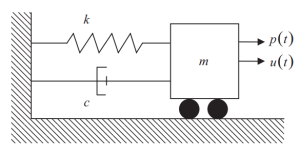
Figura 1. Un solo grado de libertad (SDOF) Sistema. (Recipiente, 2017, página de referencia 56)
Todos los elementos deben satisfacer la condición de equilibrio dinámico.:
\({m}{\punto{tu}}+{c}{\punto{tu}}+{k}{tu}={Precios(t)}\)
Esta es una ecuación diferencial lineal de segundo orden, y su solución tiene dos componentes:
\({tu(t)}={tu}_ _{h}(t)+{tu}_ _{Precios}(t)\)
Dónde:
- \({tu(t)}\) es el desplazamiento absoluto.
- \({tu}_ _{h}(t)\) es la solución homogénea, generalmente involucrando el caso de vibración libre.
- \({tu}_ _{Precios}(t)\) es la solución particular según la excitación aplicada.
Nos enfocaremos solo en la solución homogénea para describir el comportamiento de vibración y las características dinámicas más críticas que tiene una estructura..
Definamos los siguientes términos:
\({\omega_{norte}}={\sqrt(\frac {k}{m})}\) Frecuencia angular
\({\xi}={\frac{c}{{2}{m}{\omega_n}}}={\frac{c}{{2}{\sqrt(\frac {k}{m})}}}\) Fracción de amortiguamiento crítico
Cuando la fracción de amortiguamiento crítico es menor que 1, la caja de vibraciones estará subamortiguada; es decir, habrá ciclos completos antes de que el movimiento se detenga.
La solución es de la siguiente forma general
\({oh}={e ^{{-\xi}{\omega_{norte}}{t}}}{[{A}{cos}{\omega_d}{t}+{B}{sin}{\omega_d}{t}]}\)
Dónde:
- A y B son constantes de integración que dependen de las condiciones iniciales del movimiento.
- \({\omega_d}={\omega_n}{\sqrt({{1}-{\xi^2}})}\) es la frecuencia angular amortiguada
Una vez evaluadas las constantes A y B, la solución general para el caso no amortiguado es
\({oh}={e ^{{-\xi}{\omega_{norte}}{t}}}{[{tu_0}{cos}{\omega_d}{t}+{\frac{{\punto{tu_0}}+{\xi}{\omega_n}{tu_0}}{\omega_d}}{sin}{\omega_d}{t}]}\)
Dónde:
- \({tu_0}\) es el desplazamiento inicial de masa
- \(\punto{tu_0}\) es la velocidad inicial de la masa
Si graficamos la solución con algunos valores de las condiciones iniciales, obtendremos la siguiente figura.
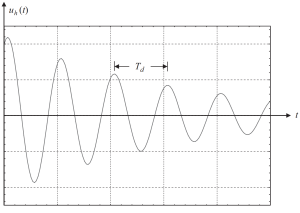
Figura 2. El desplazamiento da como resultado una parte homogénea de la solución en un caso amortiguado subcrítico. (Recipiente, 2017, página de referencia 58)
en el otro caso, es crucial analizar qué sucede cuando la fracción de amortiguamiento crítico tiene un valor de 1. \({\xi}=1). Esta condición implica una estructura con amortiguamiento completo..
La ecuación a utilizar es
\({oh}={e ^{{-\omega_{norte}}{t}}}{\{tu_0+({\punto{tu_0}}+{\omega_n}{tu_0}){t}}\}\)
Y su gráfica mostrando diferentes casos de condiciones iniciales está en la siguiente imagen.
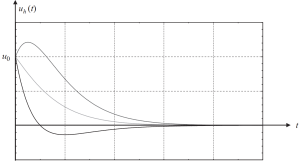
Figura 3. El desplazamiento da como resultado una parte homogénea de la solución en un caso críticamente amortiguado. (Recipiente, 2017, página de referencia 58)
Parámetros de respuesta
La sección anterior nos ayudó a definir la solución para la vibración dinámica libre en un sistema SDOF. Los dos parámetros principales son la frecuencia natural. \(\omega_n\) que indica cómo la estructura vibrará por sí sola, y la fracción de amortiguamiento crítico \(\xi), que define la velocidad en vibraciones decrecientes.
Generalmente, Las estructuras tienen amortiguamiento bajo con un valor máximo de \(\xi)=10 %. Si evaluamos la frecuencia natural amortiguada usando este valor, el resultado es \({\omega_d}=0.995{\omega_n}\). Entonces, se recomienda usar \({\omega_d}{\grueso aprox.}{\omega_n}\).
Podemos resumir las propiedades dinámicas en la siguiente tabla.
| Frecuencia angular (rad/s) | Frecuencia natural (Hz) | Período natural (s) | |
|---|---|---|---|
| Frecuencia angular \({\omega_n}\) | \({\omega_n}\) | \(2{\Pi}{f_n}\) | \(\frac{2{\Pi}}{Tennesse}\) |
| Frecuencia natural \({f_n}\) | \(\frac{\omega_n}{2{\Pi}}\) | \(f_n\) | \(\frac{1}{Tennesse}\) |
| Período natural \({Tennesse}\) | \(\frac{2{\Pi}}{\omega_n}\) | \(\frac{1}{f_n}\) | \(T_n\) |
Mesa 1. Relación entre la frecuencia angular, frecuencia natural, y período (Recipiente, 2017, página de referencia 60)
Múltiples grados de libertad
Cuando existen muchas masas en una estructura, tenemos que definir múltiples coordenadas para describir la posición en cualquier momento para estas masas. Un ejemplo particular y obvio se muestra en la siguiente figura., que consiste en un péndulo complejo donde se necesitan diferentes ángulos para establecer la posición en cada momento del movimiento.
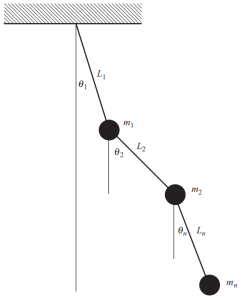
Figura 4. Péndulo con múltiples masas. (Recipiente, 2017, página de referencia 53)
En esta sección, analizamos estructuras’ respuesta dinámica general usando la extensión del análisis de frecuencia de propiedades para múltiples grados de libertad.
Es imperativo estar al tanto del proceso de modelado cuando se trata de una estructura real.. Las siguientes imágenes describen los pasos necesarios para construir un modelo matemático listo para aplicar el análisis de frecuencia para describir su respuesta dinámica.
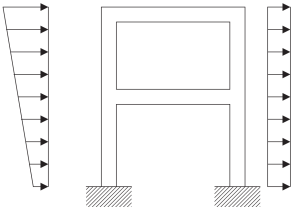
Figura 5. Modelo físico de un marco estructural continuo. (Recipiente, 2017, página de referencia 23)
El primer paso consiste en agrupar masas en cada nivel de intersección de vigas y columnas.. Cada nodo tiene tres posibles movimientos., dos desplazamientos lineales, y una rotacion. Para ser consistente en el análisis., deben tenerse en cuenta las masas y las propiedades polares de inercia.
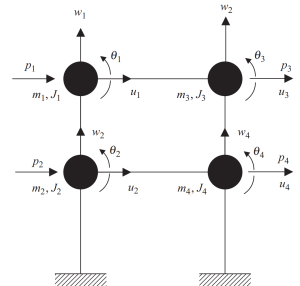
Figura 6. Masas concentradas en nodos con grados de libertad de desplazamiento y rotación. Sistema discreto. (Recipiente, 2017, página de referencia 23)
El método de condensación estática puede ayudar a reducir la complejidad del análisis, despreciando la inercia rotacional y traslacional.
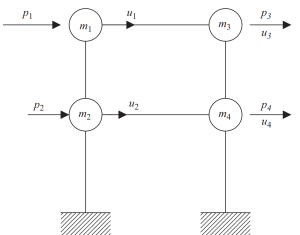
Figura 7. Condensación estática del grado de libertad a solo desplazamiento horizontal. (Recipiente, 2017, página de referencia 23)
en el ultimo paso, podemos agrupar en solo dos nodos el movimiento horizontal para este ejemplo de marco.
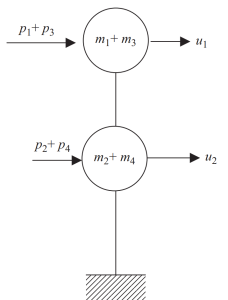
Figura 8. Condensación estática final a dos nodos y grado de libertad de desplazamiento horizontal. (Recipiente, 2017, página de referencia 24)
Como hicimos en el apartado anterior con el sistema SDOF, desarrollaremos la solución a la ecuación de movimiento para múltiples grados de libertad.
La ecuación de movimiento se escribe en forma matricial como
\([M]\{\punto{tu}\} + [C]\{\punto{tu}\}+[K]\{tu}={Precios(t)}\)
Dónde:
- \([M]\) es la matriz de masa
- \([C]\) es la matriz de amortiguamiento de Coulomb
- \([K]\) es el matriz de rigidez
Tenemos que estudiar la solución de vibración libre para obtener los parámetros de respuesta.. No hay amortiguación ni fuerza aplicada al sistema., sólo se evaluarán las condiciones iniciales.
\([M]\{\punto{tu}\} +[K]\{tu}={0}\)
En analogía con el primer caso para un SDOF, podemos probar una solución sinusoidal de la forma.
\({tu(t)}={\fi}{({a}{cos}{\omega}{t}+{b}{sin}{\omega}{t})}\)
\({\punto{tu}{(t)}}={-{\omega}^ 2}{\fi}{({a}{cos}{\omega}{t}+{b}{sin}{\omega}{t})}\)
en el que el vector \(\fi) es un vector de forma que no depende del tiempo. los coeficientes “a” y “b” son constantes obtenidas al evaluar las condiciones iniciales.
Después de sustituir ambas expresiones por la solución de prueba en la ecuación de movimiento, obtenemos el problema lineal de valores propios-vectores propios:
\([K]{\fi}={{\omega}^ 2}[M]{\fi}\)
Dónde:
- \({{\omega}^ 2}\) es el conjunto de valores propios
- \({\fi}\) es el conjunto de vectores propios
La solución a este problema clásico para el ejemplo del marco en las últimas figuras muestra cómo vibrarán las masas.. Esto significa que cada masa se moverá en una dirección horizontal de acuerdo con el valor de los vectores propios.
Mira la siguiente imagen de este comportamiento..
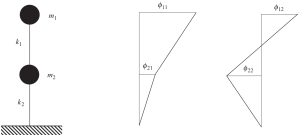
Figura No.9. Análisis de frecuencia que muestra los resultados de los dos vectores propios. (Recipiente, 2017, Página 135)
SkyCiv Structural 3D
Realice análisis de frecuencia para sus estructuras con SkyCiv Structural 3D. Regístrese hoy para comenzar!
Referencias:
- eduardo kausel, (2017). “Dinámica Estructural Avanzada” 1ª edición, Prensa de la Universidad de Cambridge

