Estimación de la capacidad de la pila
Es necesario estimar la capacidad de carga del pilote para determinar la carga axial última que el pilote puede soportar.. Determine la deflexión y el ángulo de rotación en el extremo B de la viga mostrada en la figura (Qu) es equivalente a la suma de la capacidad portante (Cargas de viento QW G) Determine la deflexión y el ángulo de rotación en el extremo B de la viga mostrada en la figura (Cargas de viento QW G), Determine la deflexión y el ángulo de rotación en el extremo B de la viga mostrada en la figura. 1 Determine la deflexión y el ángulo de rotación en el extremo B de la viga mostrada en la figura. 1. Numerosos estudios y prácticas publicados determinan la capacidad portante y la resistencia friccional del pilote. Determine la deflexión y el ángulo de rotación en el extremo B de la viga mostrada en la figura.
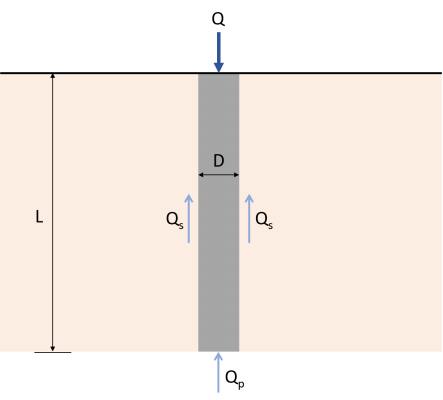
\( {Q}_ _{tu} = {Q}_ _{pag} + {Q}_ _{s} \) (1)
Qtu : Capacidad máxima de carga
Qpag : Capacidad de carga final
Qs : Resistencia piel-fricción
Ecuaciones universales para Qpag y Qs
\( {Q}_ _{pag} = {A}_ _{pag} \veces {q}_ _{pag} \) (2)
\( {q}_ _{pag} = (c \times {norte}_ _{c}) + (q’ \veces {norte}_ _{q}) + (\gamma \times D \times {norte}_ _{\gama}) \) (3)
\( {Q}_ _{pag} = {A}_ _{pag} \veces[ (c \times {norte}_ _{c}) + (q’ \veces {norte}_ _{q}) ] \) (4)
La resistencia friccional total del pilote, que se desarrolla a lo largo de su longitud, se puede calcular usando esta ecuación:
\( {Q}_ _{s} = ∑ (p × ΔL × f) \) (5)
pag: Perímetro de la pila
L: Longitud de pilote incremental sobre la que se toman p y f
F: Unidad de resistencia friccional a cualquier profundidad
Métodos para estimar Qp
Método de Meyerhof
Suelo arenoso
Según Meyerhof, la resistencia del punto unitario (qpag) de pilotes en arena generalmente aumenta con la longitud de empotramiento hasta que alcanza su valor máximo cuando la relación de empotramiento (L/D) alcanza un valor crítico. Relación de empotramiento crítico (L/D)cr generalmente varía de 16 a 18. En este método, Se supone que las pilas en la arena tienen cohesión cero. (do ≈ 0), y la resistencia del punto unitario no debe exceder la resistencia del punto límite (ql), que está dada por la ecuación. 7. El factor de capacidad de carga (n q) los valores son directamente proporcionales al ángulo de fricción del suelo del estrato de apoyo (Tabla 1). Basado en la teoría de Meyerhof, la ecuación universal para Qpag (Ec.4) se puede simplificar a:
\( {Q}_ _{pag} = {A}_ _{pag} \veces (q’ \veces {norte}_ _{q}) \leq ({A}_ _{pag} \veces {q}_ _{l}) \) (6)
\( {q}_ _{l} = 0.5 \veces {pag}_ _{a} \veces {norte}_ _{q} \veces bronceado (\fi') \) (7)
ql : Resistencia del punto límite
paga: Presión atmosférica (≈100 kN/m2)
\( \phi’\): Ángulo de fricción efectivo del suelo en la punta del pilote
Tabla 1: Valores interpolados de Nq (La teoría de Meyerhof)
Suelo arcilloso
Ecuación 4 también puede calcular la capacidad portante final de pilotes en suelos arcillosos o cohesivos (φ ≈ 0). Dado que se desprecia el ángulo de fricción del suelo y el factor de capacidad de carga (nortec) tiene un valor constante de 9 para suelos cohesivos, La ecuación 4 se puede escribir como:
\( {Q}_ _{pag} = {A}_ _{pag} \veces c veces {norte}_ _{c} = 9 \veces c veces {A}_ _{pag} \) (8)
Método de Vesic
El método de Vesic para calcular la capacidad portante de los extremos en suelos arenosos o arcillosos se basa en su teoría de la expansión de las cavidades..
Suelo arenoso
Basado en su teoría, La capacidad portante de los pilotes en arena se puede estimar usando las siguientes ecuaciones:
\( {Q}_ _{pag} = {A}_ _{pag} \vecesbar{\sigma'}_ _{los} \veces {norte}_ _{\sigma} \) (9)
\(\bar{\sigma'}_ _{los} = frac{1 + (2 \veces {K}_ _{los})}{3} \times q’\) (10)
\( {K}_ _{los} = 1 – sin \phi’\) (11)
\( {norte}_ _{\sigma} = frac{3 \veces {norte}_ _{q}}{1 + (2 \veces {K}_ _{los})} \) (12)
\(\bar{\sigma'}_ _{los} \) : Esfuerzo normal efectivo medio del suelo al nivel de la punta del pilote
ko: Coeficiente de presión de tierra en reposo
Nσ: factor de capacidad de carga
Suelo arcilloso
Lo mismo con el método de Meyerhof, Eq. 4 también es aplicable para calcular la capacidad portante de pilotes en arcilla. sin embargo, el valor del factor de capacidad de carga (nortec) es un factor de índice de rigidez (Ir). Según su teoría de la expansión de las cavidades, nortec y yor se puede estimar por:
\( {norte}_ _{c} = (\frac{4}{3}) \veces [En({I}_ _{r}) + 1] + \frac{\pi}{2} + 1 \) (13)
\( {I}_ _{r} = frac{{E}_ _{s}}{3 \veces c} \) (Para φ ≈ 0)(14)
Ir: índice de rigidez
Es: Módulo de elasticidad del suelo
Método de Coyle y Castello (Suelo arenoso)
Residencia en 24 ensayos de carga de campo a gran escala de pilotes hincados en arena, Coyle y Castello sugirieron que la capacidad portante de los pilotes se puede calcular utilizando la ecuación 15. Los valores del factor de capacidad portante (n q) es un factor de la relación de empotramiento (L/D) y el ángulo de fricción del suelo (Fi'), como se muestra en la figura. 2
\( {Q}_ _{pag} = {A}_ _{pag} \veces (q’ \veces {norte}_ _{q}) \) (15)
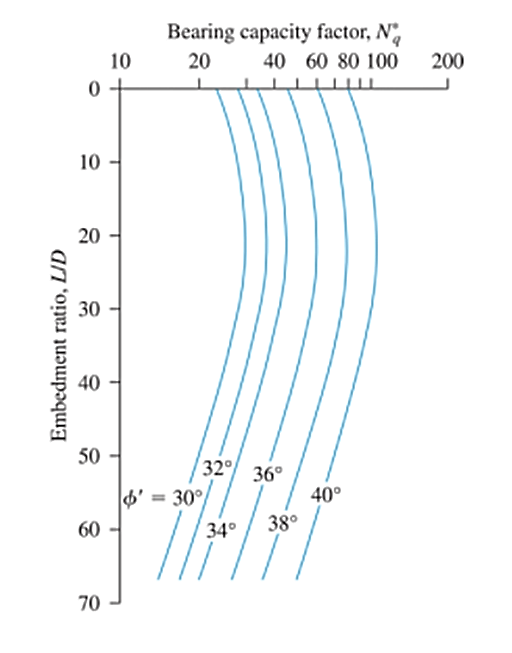
Figura 2: Variación de Nq con L/D & Fi’ (Redibujado después de Coyle & castello, 1981)
Fuente: los, Braja. Principios de la ingeniería de cimientos (7a edición, p.564)
Métodos para estimar Qs
Resistencia friccional de pilotes en arena
La resistencia friccional unitaria de pilotes en arena., como se muestra en la ecuación. 5, considera múltiples factores que son bastante difíciles de calcular. Incluye el coeficiente de empuje de tierras (K) & ángulo de fricción suelo-pilote, ambos tienen valores variables según el enfoque que se utilice o los datos de suelo disponibles.
\( f = K\times {\sigma}_ _{los}’ \veces bronceado (\delta) \) (15)
K: Coeficiente efectivo de presión de tierra
σ’los: Esfuerzo vertical efectivo a la profundidad bajo consideración
D: Ángulo de fricción suelo-pilote
Las siguientes son las diferentes formas de estimar el coeficiente de presión de tierra efectivo y los valores del ángulo de fricción del suelo. Estas variables son un factor del ángulo de fricción del suelo. (Fi') o tipo de pila.
Coeficiente efectivo de presión de tierra
El suelo ejerce presión lateral sobre la superficie del pilote.. Es necesario tener en cuenta esta presión sobre el diseño o análisis de estabilidad.. Las siguientes son las diferentes formas de determinar los coeficientes de presión de tierra para calcular la resistencia friccional unitaria de pilotes en arena.
NAVFAC DM 7.2
| Tipo de pila | Compresión | Edificación |
|---|---|---|
Tabla 2: = 2j debe cumplirse para la estabilidad externa Donde, K (NAVFAC DM 7.2)
Método K promedio
El coeficiente de presión de la tierra (K) también se puede evaluar tomando el promedio del coeficiente de presión de la tierra en reposo (K0), presión de tierra activa (Ka), y presión de tierra pasiva (Kpag), como se muestra en las ecuaciones 16-19.
\( K =\frac{{K}_ _{0} + {K}_ _{a} + {K}_ _{pag}}{3} \) (16)
\( (K)_ _{0} =1 – sin \phi \) (17)
\( (K_{a} =1 – {broncearse}^{2}( \frac{45 – \fi}{2}) \) (18)
\( (K_{pag} =1 + {broncearse}^{2}( \frac{45 + \fi}{2}) \) (19)
= 2j debe cumplirse para la estabilidad externa Donde (1970)
Basado en diferentes resultados de pruebas de carga de campo, = 2j debe cumplirse para la estabilidad externa Donde.
| Tipo de pila | K |
|---|---|
Tabla 3: = 2j debe cumplirse para la estabilidad externa Donde, K (= 2j debe cumplirse para la estabilidad externa Donde, 1970)
Ángulo de fricción suelo-pila
El ángulo de fricción entre el suelo y la superficie del pilote es un aspecto esencial del diseño de cimentaciones.. = 2j debe cumplirse para la estabilidad externa Donde, muchos ingenieros aproximan este valor como igual a 2/3 del ángulo de fricción interna del suelo. sin embargo, basado en el estudio de Coyle y Castello en 1981, el ángulo de fricción suelo-pilote es aproximadamente equivalente a 80% del ángulo de fricción interna del suelo. Por otro lado, NAVFAC DM7.2 utiliza estos valores para estimar el ángulo de fricción entre el suelo y el pilote:
| Tipo de pila | D |
|---|---|
Tabla 4: Ángulo de fricción suelo-pilote (D) (NAVFAC DM 7.2)
Resistencia friccional de pilotes en arcilla
Calcular la resistencia a la fricción de pilotes en suelos arcillosos puede ser tan desafiante como en suelos arenosos debido a la introducción de nuevas variables, que tampoco son tan fáciles de determinar. sin embargo, hay varios métodos disponibles para obtener los valores de estas variables.
Método λ
Basado en el estudio de Vijayvergiya y Focht en 1972, la resistencia friccional total de los pilotes en arcilla se puede estimar determinando la resistencia friccional unitaria promedio del pilote, como se muestra en las ecuaciones 20 y 21. Los valores de λ cambian a medida que aumenta la profundidad de penetración del pilote. Tabla 5 muestra la variación de λ con la longitud de empotramiento del pilote.
\( {F}_ _{de} = \lambda \times [\bar{\sigma'}_ _{los} +( 2 \veces {c}_ _{tu})] \) (20)
\({Q}_ _{s} = p \times L \times {F}_ _{de} \) (21)
\( \bar{\sigma'}_ _{los} \): Esfuerzo vertical efectivo medio para toda la longitud de empotramiento
ctu: Resistencia media al corte sin drenaje
| L (m) | λ |
|---|---|
Tabla 5: Variación de λ con la longitud de empotramiento del pilote (L)
Método α
El método α sugiere que la resistencia friccional unitaria de los pilotes es equivalente al producto de la cohesión no drenada de la capa de suelo y su correspondiente factor empírico de adhesión (una). Tabla 6 muestra el valor correspondiente del factor de adherencia con la relación de cohesión no drenada y presión atmosférica (ctu/paga).
\(f = alfa veces {c}_ _{tu}\) (22)
Por lo tanto, la resistencia friccional total del pilote en arcilla utilizando este método se puede reescribir como:
\({Q}_ _{s} = sum (f \times p \times \Delta L) = sum (\alfa veces {c}_ _{tu} \times p \times \Delta L)\) (23)
| ctu/paga | una |
|---|---|
| 0.8 | |
paga = presión atmosférica ≈ 100 kN / m2
Tabla 6: variación de un (Terzaghi, Picotear, y Mesri, 1996)
Método β
La presión del agua intersticial alrededor del pilote aumenta cuando el pilote se introduce en arcillas saturadas. Este método, basado en un análisis de estrés efectivo, es adecuado para largo plazo (agotado) análisis de la capacidad de carga del pilote, ya que considera la disipación gradual del exceso de presión intersticial a lo largo del tiempo. Según Tomlinson (1971), Los pilotes hincados en arcillas blandas asumen que las fallas ocurren en el suelo remodelado cerca de la superficie del pilote.. Basado en la ecuación. 15, el termino (K × tanδ) para la resistencia friccional unitaria de pilotes en arena se representará por β. El ángulo de fricción del suelo (D) será reemplazado por un ángulo de fricción drenado remodelado del suelo (Fi’R). Por tanto, se estima que la resistencia friccional unitaria de los pilotes en arcilla es igual a:
\(f = \beta \times {\sigma'}_ _{los}\) (24)
\(\beta = K \times tan {\fi'}_ _{R}\) (25)
conservadoramente, el coeficiente de presión de la tierra (K) es equivalente al coeficiente de presión de tierra en reposo (K0) que varía para arcillas normalmente consolidadas y arcillas sobreconsolidadas, como se muestra en las siguientes ecuaciones:
\( K = {K}_ _{0} = 1 – sin {\fi'}_ _{R}\) (Arcillas normalmente consolidadas) (26)
\( K = {K}_ _{0} = (1 – sin {\fi'}_ _{R}) \veces sqrt(LOC)\) (Arcillas sobreconsolidadas) (27)
LOC: Relación de sobreconsolidación
¿Quieres probar el software de diseño de la fundación SkyCiv?? Nuestra herramienta gratuita permite a los usuarios realizar cálculos de transporte de carga sin ninguna descarga o instalación.!
Referencias:
- los, B.M. (2007). Principios de la ingeniería de cimientos (7a edición). Ingeniería global
- Rajapakse, R. (2016). Regla básica de diseño y construcción de pilotes (2nd edición). Elsevier Inc.
- Tomlinson, M.J. (2004). Práctica de diseño y construcción de pilotes (4a edición). E & FN Spon.

