Este artículo analiza dos ejemplos de diseño de losas de hormigón armado., incluyendo flexión unidireccional y bidireccional. El objetivo principal es comparar los resultados obtenidos entre los cálculos manuales y el módulo de diseño de placas SkyCiv. Usaremos el Eurocódigo 2 para estructuras de hormigón armado.

Los códigos de construcción tienen enfoques similares al definir los casos típicos para losas. Si quieres aprender un poco más sobre este tema, le sugerimos leer los siguientes artículos sobre el diseño de losas Ejemplo de diseño de losa de ACI y comparación con SkyCiv y Estándares australianos AS3600 Ejemplo de diseño de losa y comparación con SkyCiv

Ejemplo de diseño de losa en una dirección

El primer caso a analizar es un pequeño edificio de una sola planta (Figura 1, Figura 2) que tiene un comportamiento de losa descrito como en una dirección.

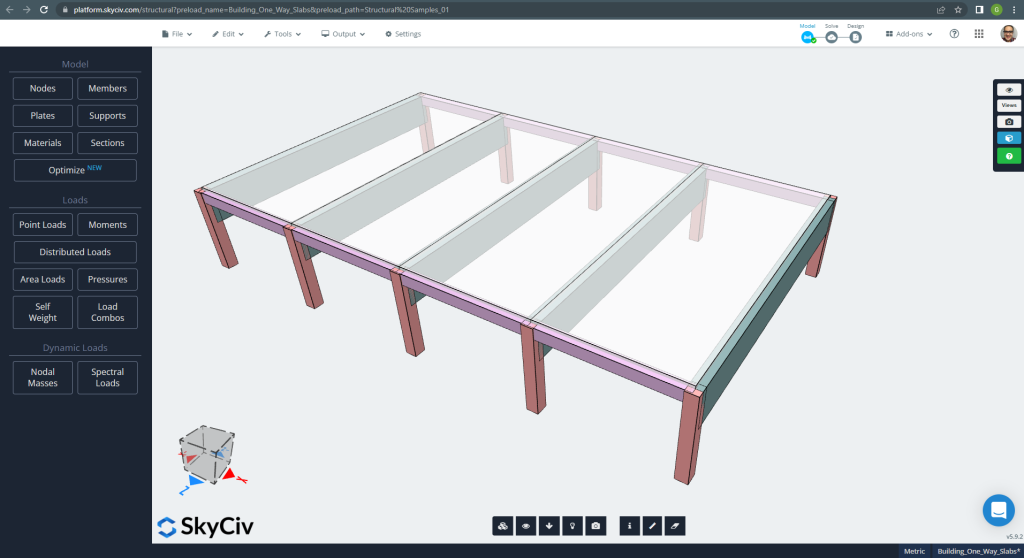
Figura 1. Ejemplo de losas unidireccionales en un edificio pequeño. (SkyCiv Estructural 3D , Ingeniería en la nube SkyCiv).

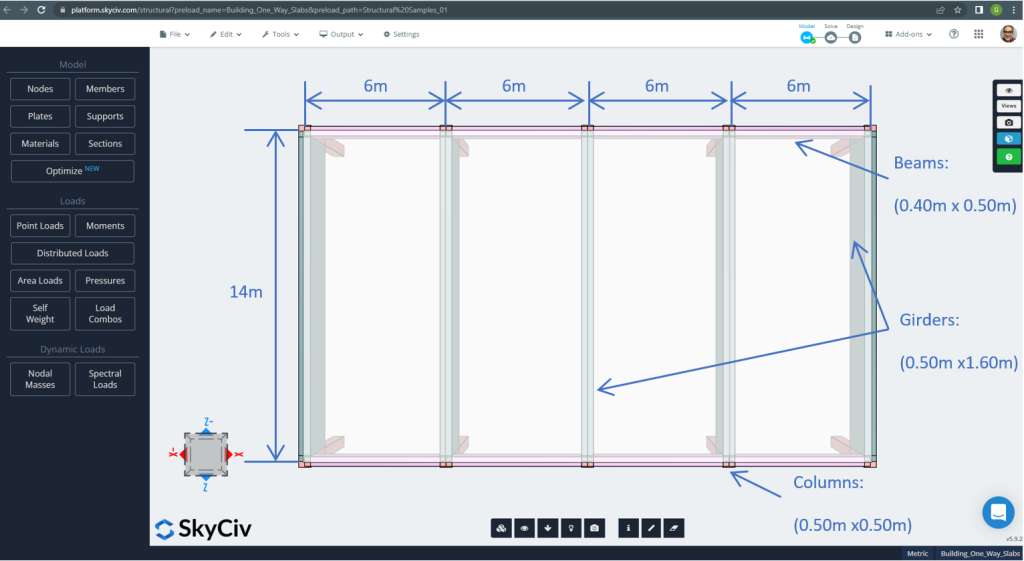
Figura 2. Ejemplo de losas unidireccionales en un edificio pequeño (dimensiones en planta). (SkyCiv Estructural 3D , Ingeniería en la nube SkyCiv).

Para el ejemplo de la losa, en resumen, el material, propiedades de los elementos, y mucho para considerar :

• Clasificación del tipo de losa: Uno – comportamiento de manera \(\frac{L_2}{L_1} > 2 ; \frac{14m}{6m}=2.33 > 2.00 \) OK!
• ocupación del edificio: uso residencial
• Espesor de losa \(A continuación se muestra un ejemplo de algunos cálculos de placa base australianos que se usan comúnmente en el diseño de placa base{losa}=0.25m)
• Densidad del hormigón armado \(\rho_w = 25 \frac{kN}{m ^ 3}\)
• Resistencia característica a la compresión del hormigón a 28 dias (C2530) \(joder = 25 MPa \)
• Peso propio de losa \(Muerto = rho_w times t_{losa} = 25 \frac{kN}{m ^ 3} \veces 0.25m = 6.25 \frac {kN}{m ^ 2}\)
• Carga muerta superpuesta \(DE = 3.0 \frac {kN}{m ^ 2}\)
• Carga viva \(L = 2.0 \frac {kN}{m ^ 2}\)

Cálculos manuales según EN-2

En esta sección, calcularemos la barra de refuerzo de acero reforzado requerida utilizando la referencia del Eurocódigo estándar. Primero se obtiene el momento flector mayorado total a realizar por la franja de ancho unitario de la losa.

• Peso muerto, \(g = (3.0 + 6.25) \frac{kN}{m ^ 2} \veces 1 m = 9.25 \frac{kN}{m}\)
• Carga viva, \(q = (2.0) \frac{kN}{m ^ 2} \veces 1 m = 2.0 \frac{kN}{m}\)
• Carga última, \(Fd = 1.35\times g + 1.5\veces q = (1.35\veces 9.25 + 1.5\veces 2.0)\frac{kN}{m} =15.5 \frac{kN}{m} \)

Antes de obtener el área de refuerzo de acero, tenemos que verificar las relaciones de profundidad efectiva de la luz. Dos casos principales:

Sistema estructural		Relación básica de profundidad efectiva de tramo
	Factor para sistema estructural K	Concreto altamente estresado %(\(\ro = 1.5 )\)	Concreto ligeramente estresado %(\(\ro = 0.5 )\)
1. Luz final de viga continua o losa continua en una dirección o losa en dos direcciones continua en un lado largo	1.3	18	26
2. Luz interior de viga continua o losa unidireccional o bidireccional	1.5	20	30

El caso más crítico es para el número uno., asi que, seleccionamos una proporción de 26.

• \(A continuación se muestra un ejemplo de algunos cálculos de placa base australianos que se usan comúnmente en el diseño de placa base{min}= frac{L}{SE}+cubrir+0.5barra de puntos_{diámetro}= frac{6m}{26}+0.025m+0.5veces 12mm=0.26m \) ~ \(0.25metro). El grosor total sigue siendo adecuado., OK!

Ahora, es hora de usar la mesa para losas continuas unidireccionales:

	Condición de soporte final				En primer apoyo interior	En medio de vanos interiores	En soportes interiores
	Fijado		Continuo
	Soporte exterior	Cerca de la mitad del tramo final	soporte final	Tramo final
Momento	0	0.086Florida	–	0.075Florida	–	0.063Florida	–
			0.04Florida		0.086Florida		0.063Florida
corte	0.4F	–		–		–
			0.46F		0.6F		0.5F

Dónde:

• L es el tramo efectivo
• F es la carga última total en el vano (1.35G k + 1.5Qk; Gk es la carga muerta y Qk la carga viva, respectivamente)

Se explicará un solo caso (soporte final continuo) y el resto se mostrará en la siguiente tabla.

• \(F=Fd\times L = 15.5 \frac{kN}{m} \veces 6m = 93.0 kN \)
• \(M=0.04FL=0.04 \times 93.0 kN \times 6m= -22.32{kN}{m}\)
• \(dia = 230 mm \)
• \(K=frac{M}{{b}{re^2}{F_{ck}}}= frac{22.32\veces 10^6 {norte}{mm}}{{1000mm}\veces{(230 mm)^ 2}\veces {25 \frac{norte}{milímetro^2}}}=0.016877)
• \(l_a = 0.95 \)
• \(z=l_a \times d = 0.95\times 230mm = 218.50 mm)
• \(A_s = frac{M}{{0.87}{F_{si}}{z}}= frac{22.32\veces 10^6 {norte}{mm}}{0.87\veces 500 {norte}{milímetro^2} \veces {218.50mm} = 234.83 milímetro^2 }\)
• \(UNA_{s,min}=0.0013{b}{re}=0.0013\times 1000mm \times 230 mm =299 mm^2\)
• \(UNA_{S t}= máx.(Como, UNA_{s,min}) = máx.(234.83, 299) milímetro^2 = 299 milímetro^2 \)

Momentos	Negativo Exterior Izquierdo	Positivo Exterior	Negativo Exterior Derecho	Interior Negativo Izquierdo	Interior Positivo	Interior Negativo Derecha
valor M, kN-m	22.32	35.15	41.85	48.00	35.15	35.15
K	0.0168	0.0266	0.03164	0.0362	0.0266	0.0266
z, mm	218.50	218.50	218.50	218.50	218.50	218.50
\(Como, mm^2\)	234.83	369.815	440.31	505.011	369.815	369.815
\(UNA_{s,min},mm^2\)	299.00	299.00	299.00	299.00	299.00	299.00
\(UNA_{S t} {milímetro^2}\)	299.00	369.815	440.31	505.011	369.815	369.815

El siguiente paso es calcular el acero de refuerzo de las barras de refuerzo utilizando el módulo de diseño de placas en SkyCiv. Por favor, sigue leyendo la siguiente sección!.

Si eres nuevo en SkyCiv, Regístrese y pruebe el software usted mismo!

Regístrese en SkyCiv!

Resultados del módulo de diseño de placas SkyCiv S3D

En esta sección se trata de obtener el área de refuerzo de acero pero solo usando el software, la Módulo de diseño de placas. de manera concisa, solo mostraremos los resultados o información importante a través de imágenes.

Antes de analizar el modelo, debemos definir un tamaño de malla de placa. Algunas referencias (2) recomendar un tamaño para el elemento shell de 1/6 del lapso corto o 1/8 del largo lapso, el más corto de ellos. Siguiendo este valor, tenemos \(\frac{L2}{6}= frac{6m}{6} = 1 metro \) o \(\frac{L1}{8}= frac{14m}{8}= 1,75 m \); tomamos 1 m como tamaño máximo recomendado y 0,50 m de malla aplicada.

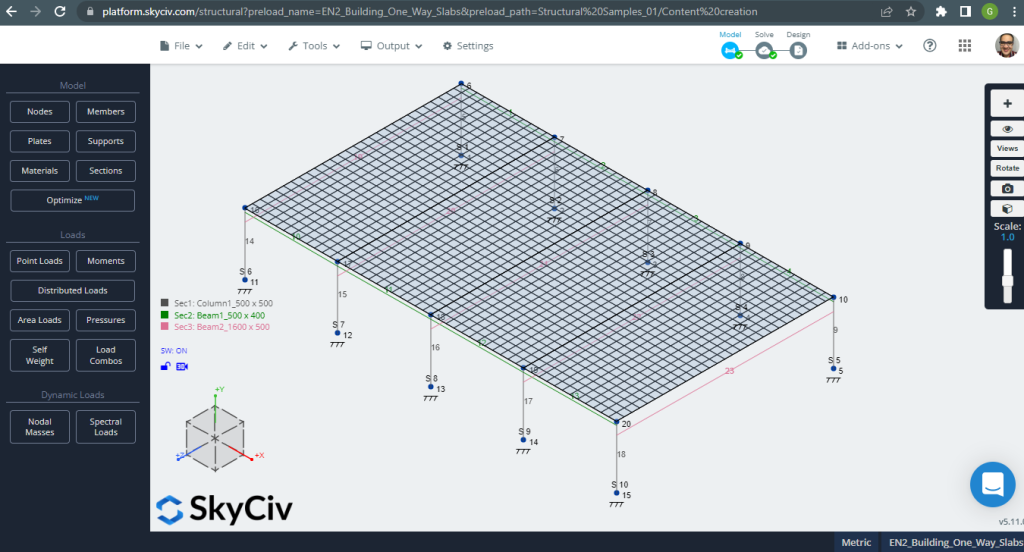
Figura 3. Placa mallada. (SkyCiv Estructural 3D , Ingeniería en la nube SkyCiv).

Una vez que mejoramos nuestro modelo estructural analítico, realizamos un análisis elástico lineal. Al diseñar losas, tenemos que comprobar si los desplazamientos verticales son inferiores al máximo permitido por el código. Eurocódigo 2 se establece un desplazamiento vertical de máxima serviciabilidad de \(\frac{L}{250}= frac{6000mm}{250}=24,0 mm).

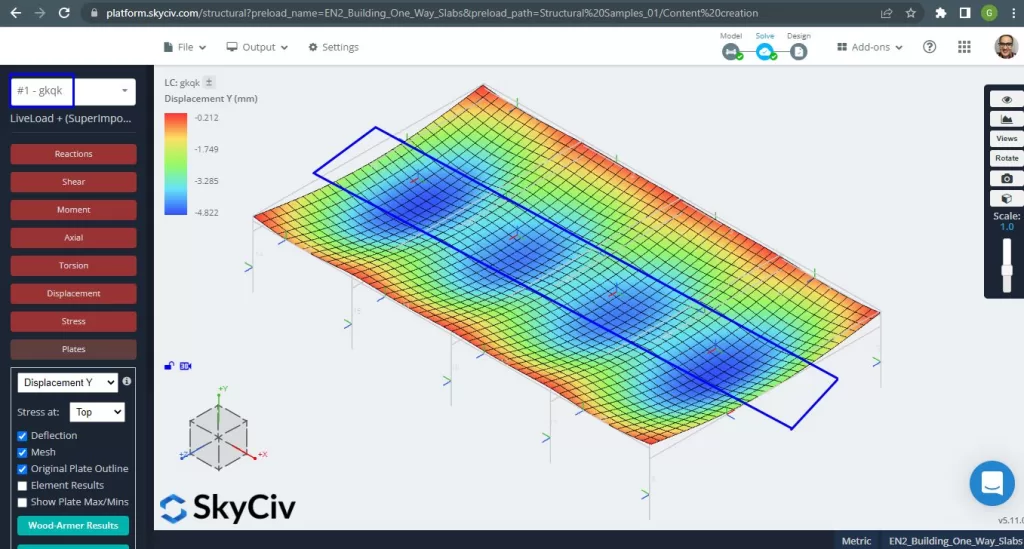
Figura 4. Desplazamiento vertical, valores máximos en el centro de los tramos. (SkyCiv Estructural 3D , Ingeniería en la nube SkyCiv).

Comparación del desplazamiento vertical máximo con el valor de referencia del código, la rigidez de la losa es adecuada. \(4.822 mm < 24.00mm).

Los momentos máximos en los vanos de la losa se ubican para positivo en el centro y para negativo en los apoyos exterior e interior.. Veamos los valores de estos momentos en las siguientes imágenes.

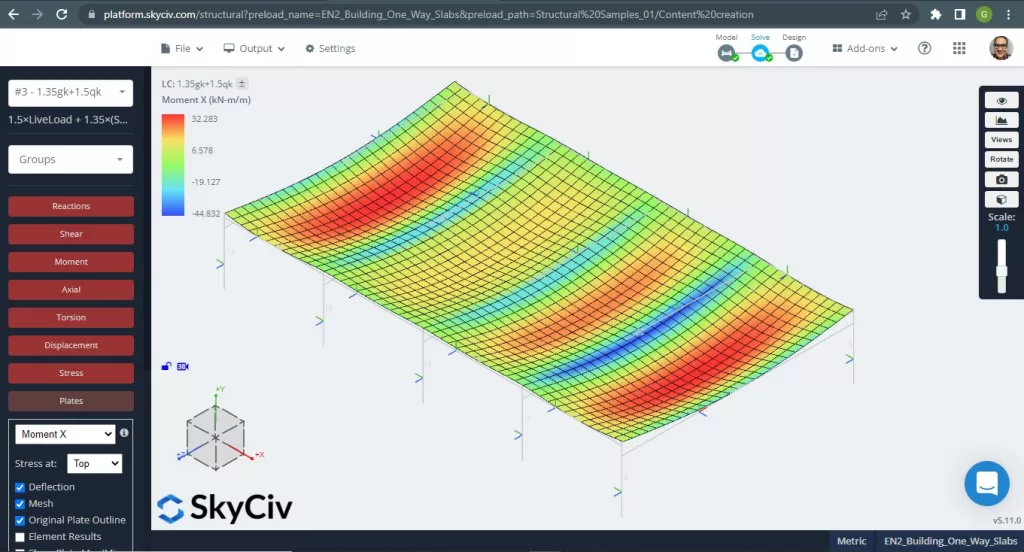
Figura 5. Momentos de flexión en la dirección X. (SkyCiv Estructural 3D , Ingeniería en la nube SkyCiv).

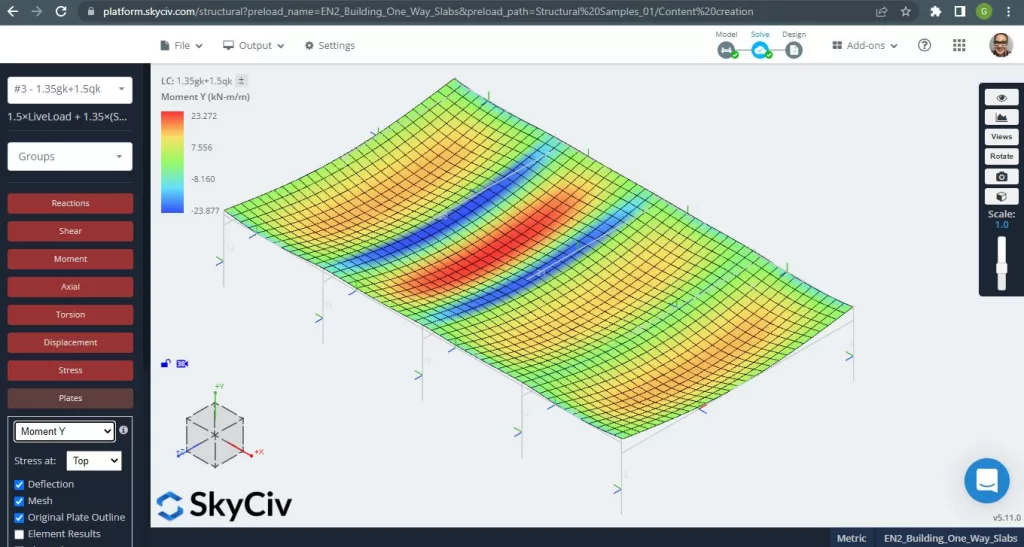
Figura 6. Momentos de flexión en la dirección Y. (SkyCiv Estructural 3D , Ingeniería en la nube SkyCiv).

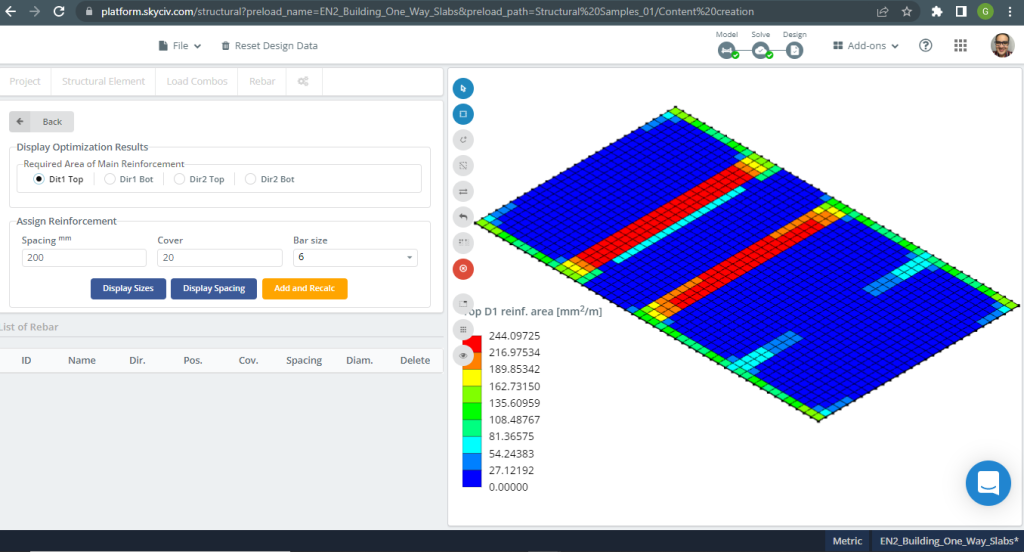
Figura 7. Refuerzo de acero para la dirección X en la parte superior. (SkyCiv Estructural 3D , Ingeniería en la nube SkyCiv).

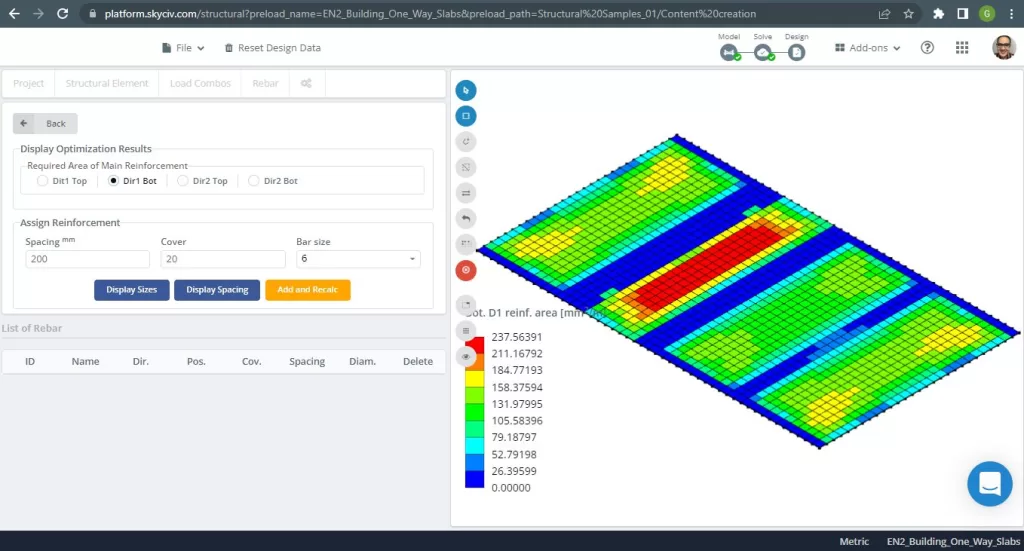
Figura 8. Refuerzo de acero para la dirección X en la parte inferior. (SkyCiv Estructural 3D , Ingeniería en la nube SkyCiv).

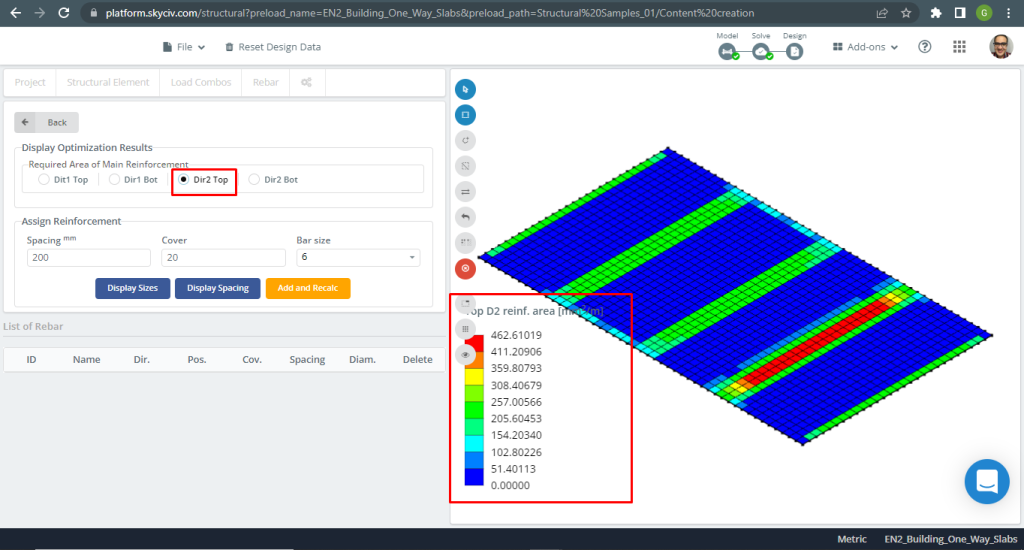
Figura 9. Refuerzo de acero para la dirección Y en la parte superior. (SkyCiv Estructural 3D , Ingeniería en la nube SkyCiv).

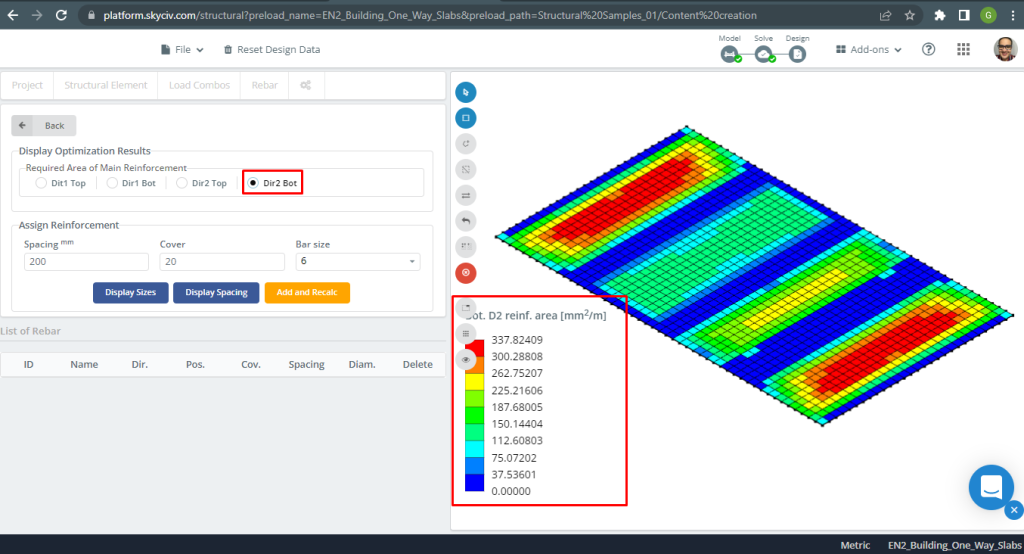
Figura 10. Refuerzo de acero para la dirección Y en la parte inferior. (SkyCiv Estructural 3D , Ingeniería en la nube SkyCiv).

Comparación de resultados

El último paso en este ejemplo de diseño de losa unidireccional es comparar el área de la barra de refuerzo de acero obtenida por análisis S3D (ejes locales “2”) y cálculos manuales.

Momentos y área de acero	Negativo Exterior Izquierdo	Positivo Exterior	Negativo Exterior Derecho	Interior Negativo Izquierdo	Interior Positivo	Interior Negativo Derecha
\(UNA_{S t, Cálculos manuales} {milímetro^2}\)	299.00	369.82	440.31	505.011	369.82	369.82
\(UNA_{S t, S3D} {milímetro^2}\)	308.41	337.82	462.61	462.61	262.75	308.41
\(\Delta_{diferencia}\) (%)	3.051	8.653	4.820	8.400	28.95	16.610

Podemos ver que los resultados de los valores están muy cerca uno del otro. Esto significa que los cálculos son correctos.!

Si eres nuevo en SkyCiv, Regístrese y pruebe el software usted mismo!

Regístrese en SkyCiv!

Ejemplo de diseño de losa en dos direcciones

SkyCiv 3D Plate Design Module es un poderoso software que puede analizar y diseñar cualquier tipo de edificio que pueda imaginar. Para el segundo ejemplo de losa de diseño, hemos decidido ejecutar un sistema de losa plana (figura 11).

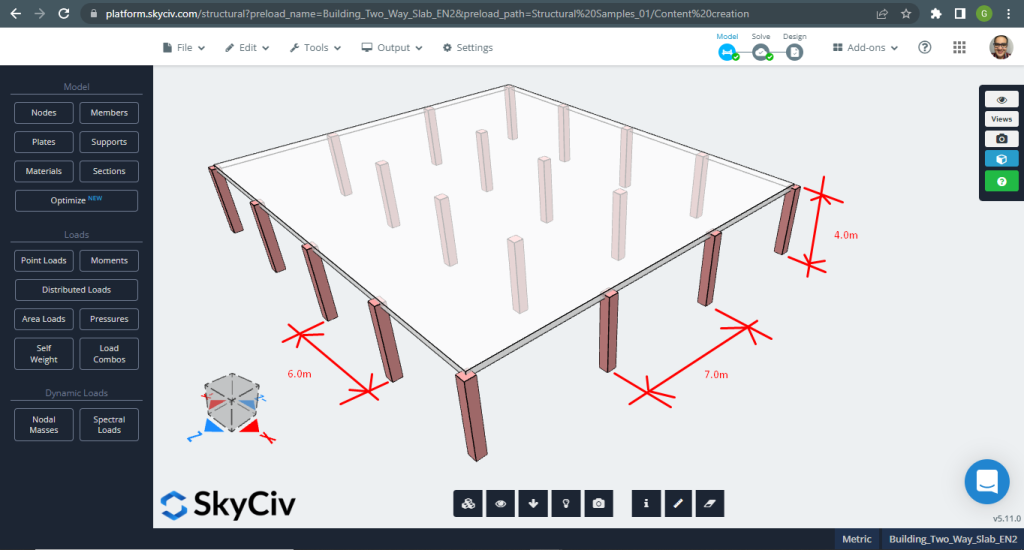
Figura 11. Ejemplo de losas unidireccionales en un edificio pequeño. (SkyCiv Estructural 3D , Ingeniería en la nube SkyCiv).

Para el ejemplo de la losa, en resumen, el material, propiedades de los elementos, y mucho para considerar :

• Clasificación del tipo de losa: Dos – comportamiento de manera \(\frac{L_2}{L_1} \la 2 ; \frac{7m}{6m}=1.17 \le 2.00 \) OK!
• ocupación del edificio: uso residencial
• Espesor de losa \(A continuación se muestra un ejemplo de algunos cálculos de placa base australianos que se usan comúnmente en el diseño de placa base{losa}=0.30m\)
• Densidad del hormigón armado \(\rho_w = 25 \frac{kN}{m ^ 3}\)
• Resistencia característica a la compresión del hormigón a 28 dias (C2530) \(joder = 25 MPa \)
• Peso propio de losa \(Muerto = rho_w times t_{losa} = 25 \frac{kN}{m ^ 3} \veces 0.30m = 7.5 \frac {kN}{m ^ 2}\)
• Carga muerta superpuesta \(DE = 3.0 \frac {kN}{m ^ 2}\)
• Carga viva \(L = 2.0 \frac {kN}{m ^ 2}\)

Cálculos manuales según EN-2

El primer paso es definir la carga última total:

• Peso muerto, \(g = (3.0 + 7.5) \frac{kN}{m ^ 2} \veces 7 m = 73.50 \frac{kN}{m}\)
• Carga viva, \(q = (2.0) \frac{kN}{m ^ 2} \veces 7 m = 14.00 \frac{kN}{m}\)
• Carga última, \(Fd = 1.35\times g + 1.5\veces q = (1.35\veces 73.50 + 1.5\veces 14.00)\frac{kN}{m} =120.225 \frac{kN}{m} \)

Para cálculo manual, la estructura tiene que ser dividida en una serie de marcos equivalentes. Podemos utilizar los siguientes métodos para alcanzar este objetivo:

• Distribución de momentos (Método de cruz resistente) para análisis de cuadros.
• Método de rigidez para el análisis de marcos en computadora. Pruebe nuestro Calculadora de matriz de rigidez.
• Un método simplificado que utiliza los coeficientes de momentos para una dirección ajustado a los siguientes requisitos (Seleccionamos este método debido a la simplicidad del modelo analizado.):
  • La estabilidad lateral no depende de las conexiones losa-columna (No analizamos el edificio para cargas laterales);
  • Hay al menos tres filas de paneles de aproximadamente el mismo claro en la dirección que se está considerando (Disponemos de cuatro y tres filas de paneles en ambas direcciones principales);
  • El tamaño de la bahía supera \(30m^2\) (Nuestra área modelo es \(42m^2\)

El espesor seleccionado para el ejemplo de losa es mayor que el valor mínimo máximo de resistencia al fuego indicado en la siguiente tabla.

Resistencia al fuego estándar	Dimensiones mínimas (mm)
	Espesor de losa, hora	Distancia del eje, a
REI 60	180	15
REI 90	200	25
REI 120	200	35
REI 240	200	50

En esta sección, desarrollaremos solo los cálculos para la dirección longitudinal y la tira de columnas (siéntase libre de calcular para otra dirección, el transversal, y para tiras intermedias). Antes de profundizar en los números, primero tenemos que dividir en tiras: medio y columna. (Para más detalles sobre tiras de diseño, mira este artículo de SkyCiv: Diseño de losas con ACI-318).

• Ancho de tira de columna: \(6m/4 = 1.50m\)
• Ancho de tira medio: \(7m – 2\times 1.50m = 4.0m\)

EC2 permite asignar momentos en cada franja de diseño de acuerdo a la siguiente tabla

	Tira de columna	franja media
Momento negativo en la columna de borde	100% pero no más que \(0.17{ser}{re^2}{F_{ck}}\)	0
Momento negativo en la columna interna	60-80%	40-20%
Momento positivo en el tramo	50-70%	50-30%

Seleccionamos los porcentajes de momentos para la tira de columnas que se analiza:

• Momento negativo en la columna de borde: 100%.
• Momento negativo en la columna interna: 80%
• Momento positivo en el tramo: 70%

Cálculo de momentos de tiras de diseño total:

	Condición de soporte final				En primer apoyo interior	En medio de vanos interiores	En soportes interiores
	Fijado		Continuo
	Soporte exterior	Cerca de la mitad del tramo final	soporte final	Tramo final
Momento	0	0.086Florida	–	0.075Florida	–	0.063Florida	–
			0.04Florida		0.086Florida		0.063Florida
corte	0.4F	–		–		–
			0.46F		0.6F		0.5F

Dónde:

• L es el tramo efectivo
• F es la carga última total en el vano (1.35G k + 1.5Qk; Gk es la carga muerta y Qk la carga viva, respectivamente)

Se explicará un solo caso (soporte final continuo) y el resto se mostrará en la siguiente tabla.

• \(F=Fd\times L = 120.225 \frac{kN}{m} \veces 6m = 721.35 kN \)
• \(M=0.04FL=0.04 \times 721.35 kN \times 6m= -173.124 {kN}{m}\)
• \(dia = 280 mm \)
• \(K=frac{M}{{b}{re^2}{F_{ck}}}= frac{173.124\veces 10^6 {norte}{mm}}{{1500mm}\veces{(280 mm)^ 2}\veces {25 \frac{norte}{milímetro^2}}}=0.012637\)
• \(l_a = 0.95 \)
• \(z=l_a \times d = 0.95\times 280mm = 266.0 mm)
• \(A_s = frac{M}{{0.87}{F_{si}}{z}}= frac{173.124\veces 10^6 {norte}{mm}}{0.87\veces 500 {norte}{milímetro^2} \veces {266.0mm} = 214.0523 milímetro^2 }\)
• \(UNA_{s,min}=0.0013{b}{re}=0.0013\times 1500mm \times 280 mm =546 mm^2\)
• \(UNA_{S t}= máx.(Como, UNA_{s,min}) = máx.(234.83, 546) milímetro^2 = 299 milímetro^2 \)

Momentos	Negativo Exterior Izquierdo	Positivo Exterior	Negativo Exterior Derecho	Interior Negativo Izquierdo	Interior Positivo	Interior Negativo Derecha
valor M, kN-m	173.124	191.125	260.064	298.281	191.125	218.429
K	0.05897	0.06500	0.0884	0.101	0.06500	0.0743
z, mm	266.00	266.00	266.00	266.00	266.00	266.00
\(Como, mm^2\)	1498.366	1651.761	2247.55	2577.835	1651.761	1887.727
\(UNA_{s,min},mm^2\)	546.00	546.00	546.00	546.00	546.00	546.00
\(UNA_{S t} {milímetro^2}\)	1498.366	1651.761	2247.55	2577.835	1651.761	1887.727

El siguiente paso es calcular el acero de refuerzo de las barras de refuerzo utilizando el módulo de diseño de placas en SkyCiv. Por favor, sigue leyendo la siguiente sección!

Resultados del módulo de diseño de placas SkyCiv S3D

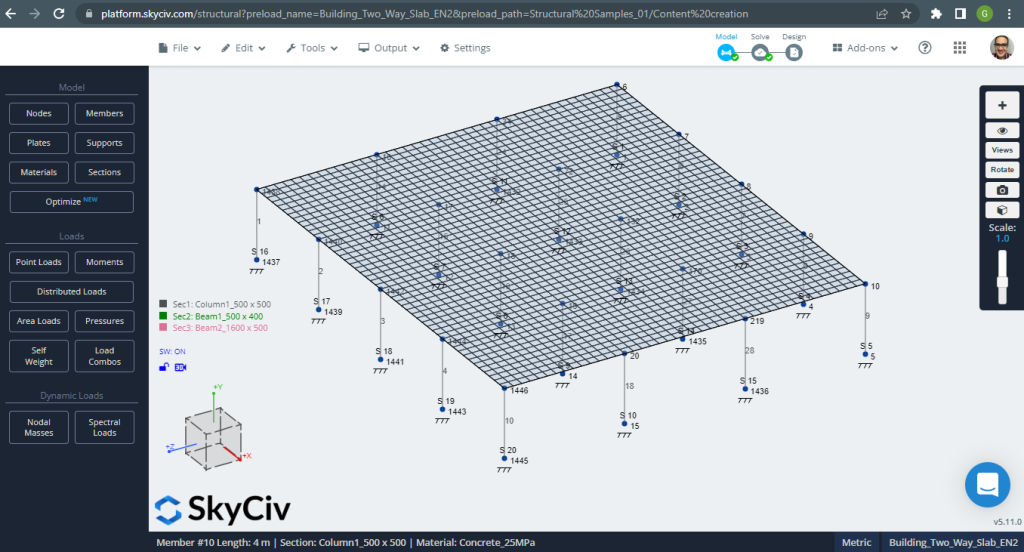
Figura 12. Ejemplo de losas unidireccionales en un edificio pequeño. (SkyCiv Estructural 3D , Ingeniería en la nube SkyCiv).

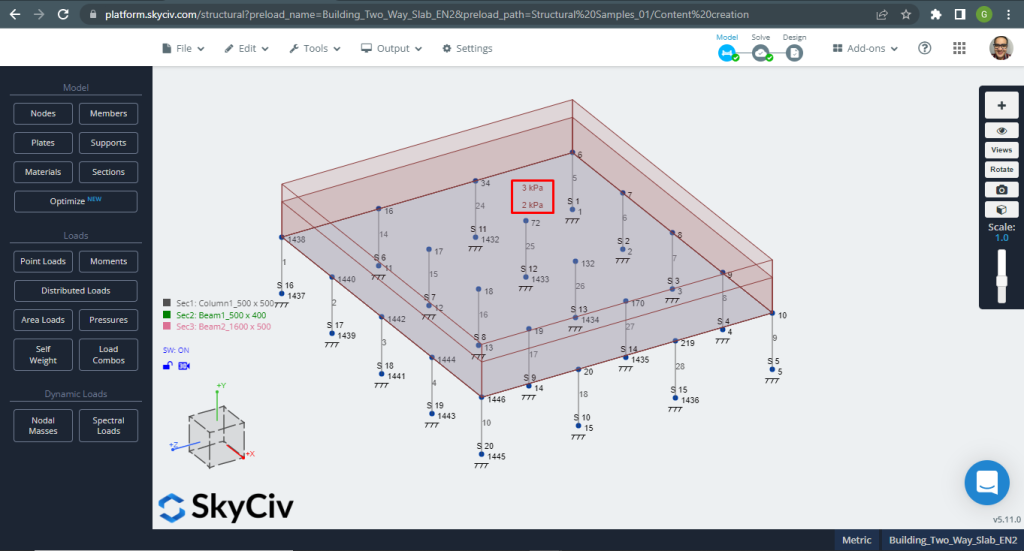
Figura 13. Ejemplo de losas unidireccionales en un edificio pequeño. (SkyCiv Estructural 3D , Ingeniería en la nube SkyCiv).

Al diseñar losas, tenemos que comprobar si los desplazamientos verticales son inferiores al máximo permitido por el código. El Eurocódigo establece un desplazamiento vertical máximo de servicio de \(\frac{L}{250}= frac{6000mm}{250}=24,0 mm).

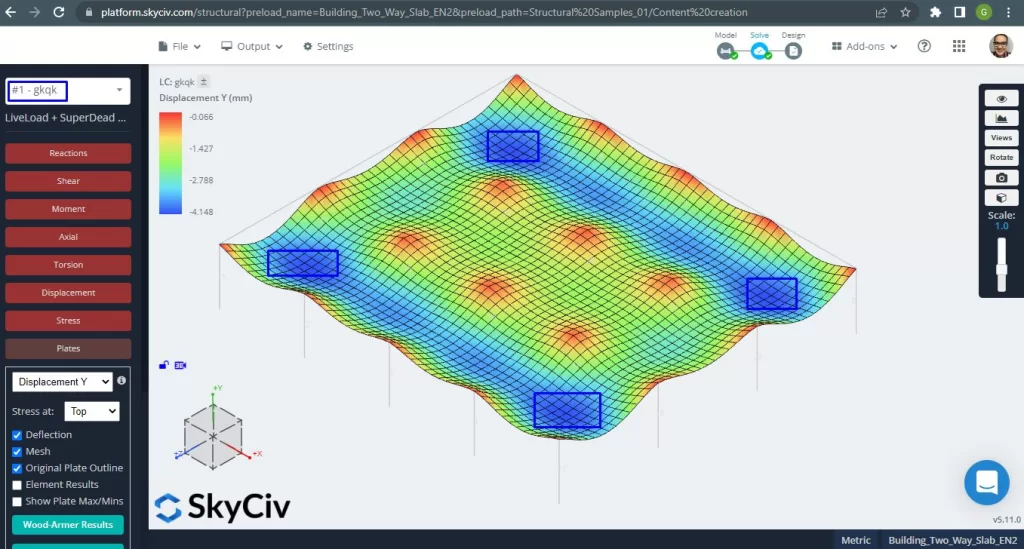
Figura 14. Ejemplo de losas unidireccionales en un edificio pequeño. (SkyCiv Estructural 3D , Ingeniería en la nube SkyCiv).

La imagen de arriba nos da el desplazamiento vertical.. El valor máximo es -4.148mm siendo menor que el máximo permitido de -24mm. Por lo tanto, la rigidez de la losa es adecuada.

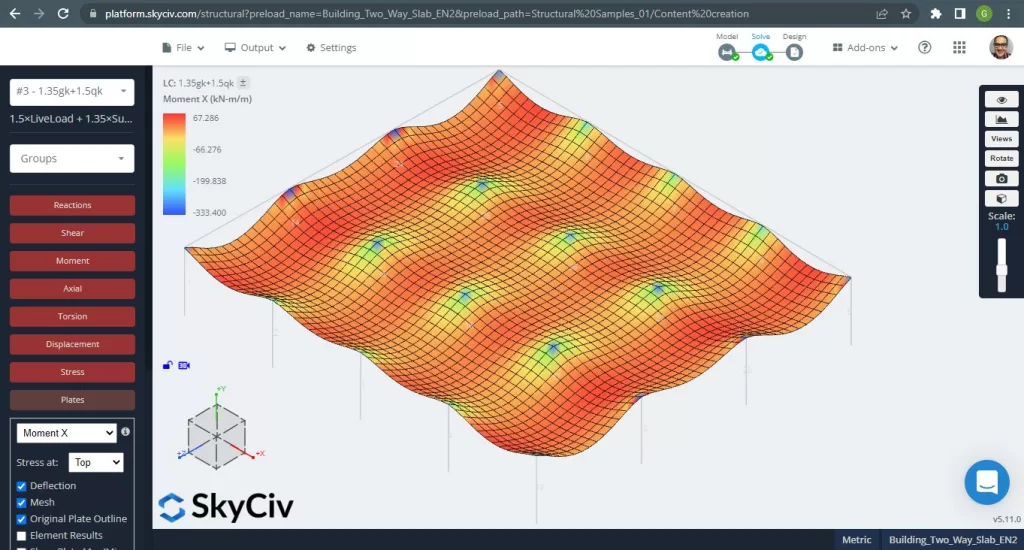
Figura 15. Ejemplo de losas unidireccionales en un edificio pequeño. (SkyCiv Estructural 3D , Ingeniería en la nube SkyCiv).

Imágenes 15 y 16 consisten en el momento de flexión en cada dirección principal. Tomando la distribución de momentos y valores, El software, SkyCiv, puede obtener entonces el área total de refuerzo de acero.

Figura 16. Ejemplo de losas unidireccionales en un edificio pequeño. (SkyCiv Estructural 3D , Ingeniería en la nube SkyCiv).

Áreas de refuerzo de acero:

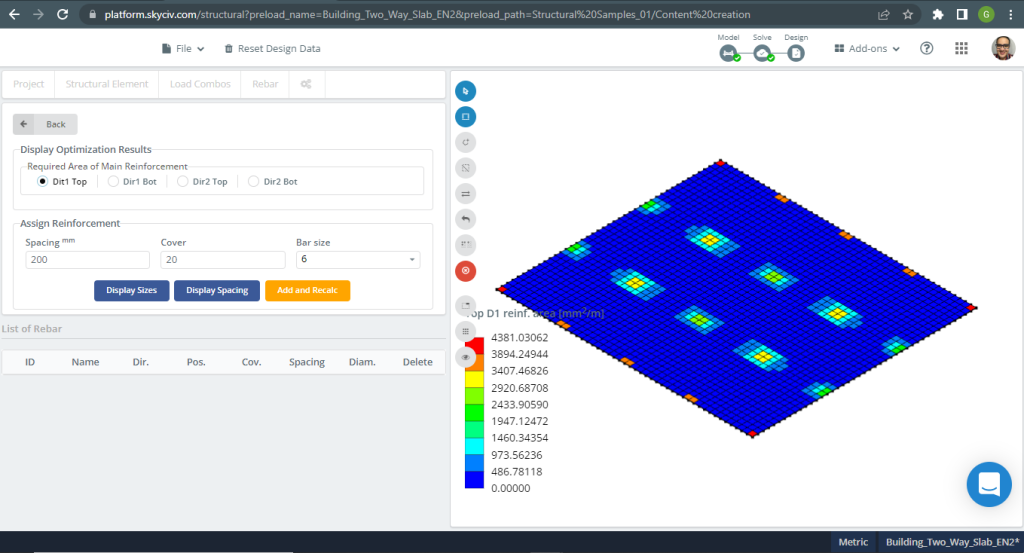
Figura 17. Ejemplo de losas unidireccionales en un edificio pequeño. (SkyCiv Estructural 3D , Ingeniería en la nube SkyCiv).

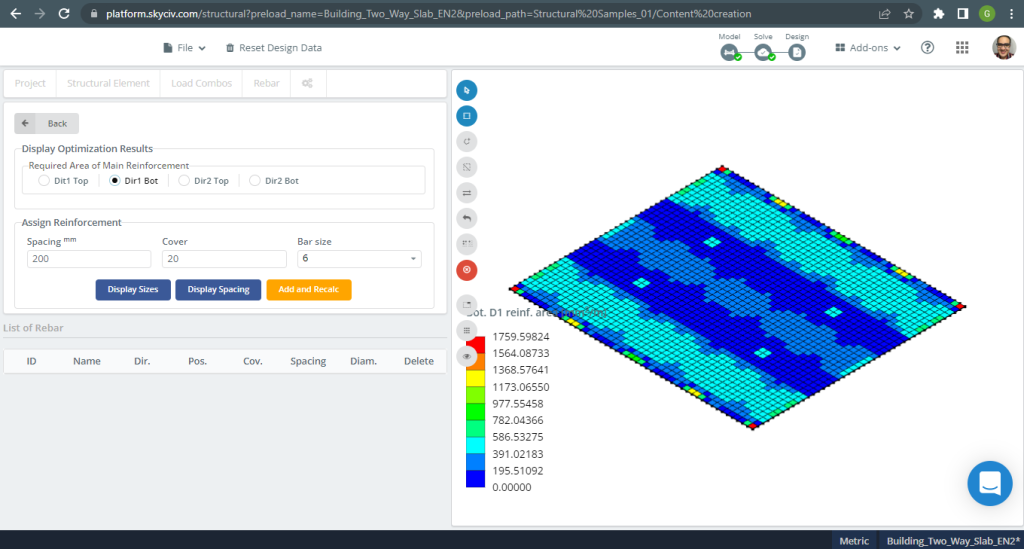
Figura 18. Ejemplo de losas unidireccionales en un edificio pequeño. (SkyCiv Estructural 3D , Ingeniería en la nube SkyCiv).

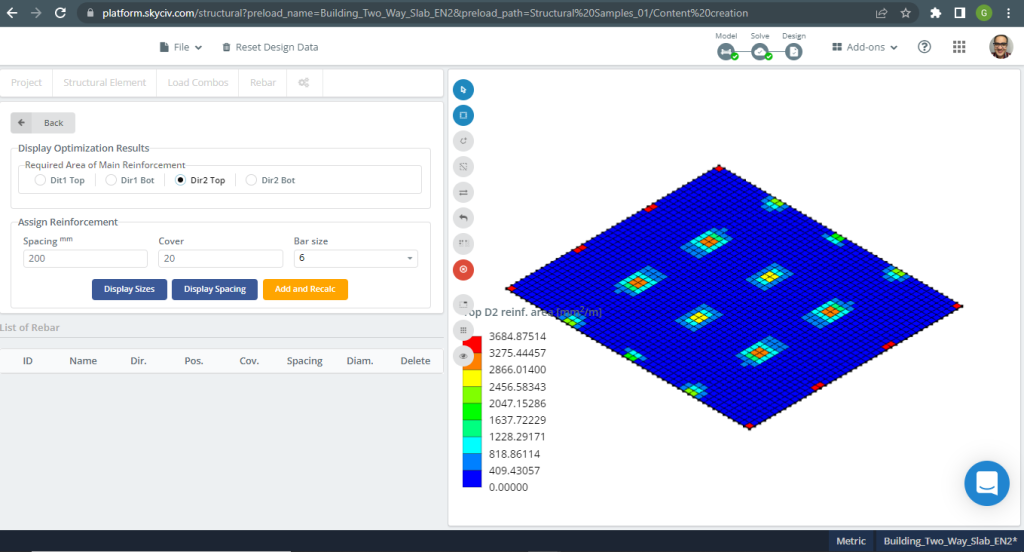
Figura 19. Ejemplo de losas unidireccionales en un edificio pequeño. (SkyCiv Estructural 3D , Ingeniería en la nube SkyCiv).

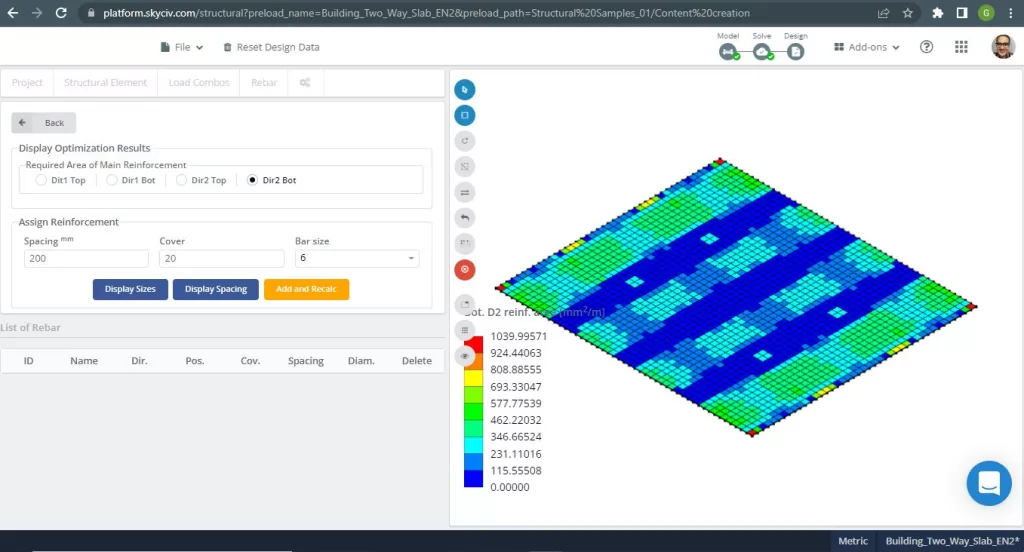
Figura 20. Ejemplo de losas unidireccionales en un edificio pequeño. (SkyCiv Estructural 3D , Ingeniería en la nube SkyCiv).

Comparación de resultados

El último paso en este ejemplo de diseño de losa en dos direcciones es comparar el área de la barra de refuerzo de acero obtenida mediante el análisis S3D y los cálculos manuales..

Barra de acero para dirección X y tira de columna

Momentos y área de acero	Negativo Exterior Izquierdo	Positivo Exterior	Negativo Exterior Derecho	Interior Negativo Izquierdo	Interior Positivo	Interior Negativo Derecha
\(UNA_{S t, Cálculos manuales} {milímetro^2}\)	1498.366	1651.761	2247.55	2577.835	1651.761	1887.727
\(UNA_{S t, S3D} {milímetro^2}\)	3889.375	1040.00	4196.145	4196.145	520.00	3175.00
\(\Delta_{diferencia}\) (%)	61.475	37.04	46.44	38.566	68.52	40.544

 

Si eres nuevo en SkyCiv, Regístrese y pruebe el software usted mismo!

Regístrese en SkyCiv!

Referencias

1. B. Mosley, R. Hulse, J H. Bungey , “Proyecto de Hormigón Armado según Eurocódigo 2”, Séptima edición, Palgrave MacMillan.
2. Bazan Enrique & Meli Piralla, “Diseño Sísmico de Estructuras”, 1ed, CLARO.
3. Eurocódigo 2: Diseño de estructuras de hormigón..