Calculadora gratis de momentos de inercia y centroides
Calcular Momento de Inercia, Centroide, y módulo de sección para una amplia variedad de figuras
Una guía completa de nuestra calculadora de momento de inercia
SkyCiv Moment of Inertia and Centroid Calculator lo ayuda a determinar el momento de inercia, centroide, y otras propiedades geométricas importantes para una variedad de formas, incluidos los rectángulos, círculos, secciones huecas, triangulos, Vigas en I, Vigas en T, ángulos y canales. También tenemos algunos artículos a continuación sobre cómo calcular el momento de inercia., así como más información sobre centroides y módulo de sección.
Puedes resolver hasta tres secciones antes de que debas registrarte para obtener una cuenta gratuita - que también te da acceso a más del software y resultados. Nuestra cuenta paga mostrará los cálculos manuales completos de cómo la herramienta llegó a este resultado. Consulte a continuación la calculadora para obtener más información sobre este tema., así como enlaces a otras herramientas y funciones útiles que SkyCiv puede ofrecerle.
¿Cómo usar la calculadora de momento de inercia de SkyCiv?
Mire el video de demostración a continuación para comenzar a usar nuestra calculadora.
Simplemente elija la forma de la sección transversal que desea evaluar de la lista desplegable, ingrese las dimensiones de la sección elegida y haga clic en Calcular.
Esta calculadora multipropósito gratuita está tomada de nuestro paquete completo de software de análisis estructural. La cual te permite:
- Calcular el momento de inercia (I) de una sección de viga (Segundo momento de área)
- Calculadora de Centroide utilizada para hallar el Centroide (C) en el eje X y Y de una sección de viga
- Calcular el primer momento de área (Momento estático de inercia) (Q) de una sección de viga
- Una calculadora de módulo de sección para determinar el módulo de sección (Z) de una sección de viga
- Calcular la constante de torsión (J) de una sección de viga
Definiciones comunes de propiedades de una sección
La calculadora del momento de inercia calculará con precisión una serie de propiedades importantes de la sección que se utilizan en la ingeniería estructural.. Aquí hay una lista concisa de los términos y definiciones de propiedades de la sección:
- Área de sección (A) – El área de la sección es un cálculo bastante simple, pero se utiliza directamente en los cálculos de esfuerzos axiales (cuanto mayor sea el área de la sección transversal, más fuerza axial)
- Momento de Inercia (Iz, Iy) – también conocido como segundo momento de área, es un cálculo utilizado para determinar la fuerza de un miembro y su resistencia contra la deflexión. Cuanto mayor sea este número, más fuerte es la sección. Hay dos ejes aquí:
- Eje mayor (Iz) – Se trata del eje Z y, por lo general, se considera el eje principal, ya que suele ser la dirección más fuerte del miembro.
- Menor Eje (Iy) - Se trata del eje Y y se considera el eje menor o débil.. Esto se debe a que las secciones no están diseñadas para soportar tanta fuerza sobre este eje.
- También vale la pena señalar que si una forma tiene las mismas dimensiones en ambas direcciones (cuadrado, circular, etc.) estos valores serán los mismos en ambas direcciones. Ver Momento de Inercia de un círculo para saber más.
- Centroide (Cz, Cy) – este es el centro de masa de la sección y generalmente tiene un componente Z y Y. Para formas simétricas, este será el centro geométrico. Para formas asimétricas (como un ángulo, Canal) estos estarán en diferentes ubicaciones. Aprende a calcular el centroide de una sección de viga. La calculadora anterior también actúa como una calculadora de centroide, calculando el centroide X y Y de cualquier tipo de forma.
- Momento estático de inercia (Qz, Qy) – También conocido como Primer Momento de Área, esto mide la distribución del área de una sección de la viga desde un eje. Como el momento de la inercia, estos están en la dirección Z y Y. Estos se utilizan normalmente en los cálculos de esfuerzos cortantes., así que cuanto mayor sea este valor, más fuerte será la sección contra el cortante.. La calculadora proporcionará este valor, pero haga clic aquí para obtener más información sobre cómo calcular el primer momento del área.
- Módulo de sección elástica (Sz, Sy en América. Zz, Zy en Gran Bretaña o Australia) – También conocido como módulo de sección estática, y se utilizan en los cálculos de esfuerzos de flexión. Por lo general, se calculan para la sección de fibras superior e inferior.. Por ejemplo, Szt es el módulo de sección sobre el eje Z a la fibra superior de la sección.
- Constante de torsión (J) - también conocido como el momento polar de inercia o J, es un valor que describe la resistencia de un material a la torsión o deformación por torsión.
- El módulo de la sección plástica (S) - una medida de la capacidad de una forma de sección transversal para resistir la flexión plástica, utilizado para estimar la tensión de un material cuando comienza a ceder (llegar a su límite plástico) bajo una carga específica y se usa típicamente para el diseño y análisis de vigas bajo carga.
Otros parámetros: estos son resultados más avanzados calculados por el generador de secciones SkyCiv completo:
- Producto de inercia (en los ejes Z y Y): Una medida de la resistencia de una forma a la rotación sobre un eje específico, igual al producto cruz de la distancia desde el eje a cualquier punto de la forma y el componente correspondiente del momento de inercia del punto.
- Módulo de sección de plástico (en los ejes Z y Y): Una medida de la capacidad de una forma de sección transversal para resistir la flexión plástica., utilizado para estimar la tensión de un material cuando comienza a ceder (llegar a su límite plástico) bajo una carga específica.
- Eje neutro plástico (en los ejes Z y Y): Un eje en una forma de sección transversal a través del cual deben pasar todas las fuerzas que actúan sobre la forma para dar como resultado una deformación plástica..
- Área de corte (en los ejes Z y Y): El área de una forma de sección transversal que es eficaz para resistir las fuerzas de corte.
- Distancia del centro de corte al centroide (tanto en el eje Z como en el eje Y): La calculadora de centroide SkyCiv ayuda a calcular la distancia entre el centro de corte y el centroide de una forma de sección transversal.
- Constante de torsión (Usando FEA): Un valor que describe la resistencia de un material a la torsión o deformación por torsión., calculado utilizando análisis de elementos finitos.
- Radio de torsión: La distancia desde un eje en el que el área de una forma de sección transversal debe concentrarse para dar como resultado la misma constante de torsión que la forma real..
- Constante de deformación: Un valor que describe la resistencia de un material a la deformación o deformación distorsionada..
- Constante de monosimetría (en los ejes Z y Y): Una medida de cuán simétrica es una forma de sección transversal con respecto a un eje específico, con un valor de cero que indica simetría perfecta.
- Radio de giro (en los ejes Z y Y): La distancia desde un eje en el que el área de una forma de sección transversal debe concentrarse para dar como resultado el mismo momento de inercia que la forma real..
- Ángulo de rotación del eje principal: El ángulo entre el eje neutral y el eje principal de una forma de sección transversal.
Acerca del momento de inercia, Centroides y otras propiedades de la sección
También hemos recopilado más información para calcular el momento de inercia de las secciones.. Esta guía completa debería ayudar a proporcionar una base de conocimientos integral para todo lo relacionado con el momento de inercia., centroides, módulo de sección y otras propiedades geométricas importantes de la sección. En los siguientes segmentos, incluimos cual es el momento de inercia, como calcular el centroide, momento de inercia y ecuaciones MOI comunes con la ayuda de SkyCiv Moment of Inertia and Centroid Calculator.
¿Qué es el momento de inercia?
El momento de inercia (más técnicamente conocido como el momento de inercia del área, o el segundo momento de área) es una propiedad geométrica importante utilizada en ingeniería estructural. Está directamente relacionado con la cantidad de resistencia del material que tiene su sección..
Generalmente hablando, cuanto mayor sea el momento de inercia, más fuerza tiene tu sección, y en consecuencia menos se deflectará bajo carga. El momento de inercia de un rectángulo, o cualquier forma para el caso, es técnicamente una medida de cuánto torque se requiere para acelerar la masa alrededor de un eje - de ahí la palabra inercia en su nombre.
Cómo encontrar el momento de inercia - Rectangular
Para calcular el momento de inercia de un rectángulo., puedes usar la fórmula:
I = (b * h ^ 3) / 12
I es el momento de inercia del rectángulo.
b es el ancho del rectángulo
h es la altura del rectángulo
Es importante notar que la unidad de medida para b y h debe ser consistente (p.ej., pulgadas, milímetros, etc.). Además, la unidad del resultado final depende de la unidad de entrada., por ejemplo, si la entrada está en metros, la unidad de resultado sería m ^ 4.
Ejemplo de cálculo del momento de inercia
Digamos que tenemos un rectángulo con las siguientes dimensiones:
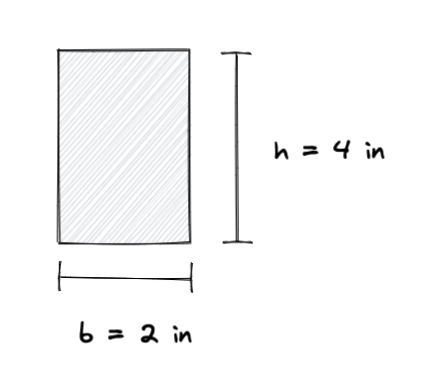
Usando la fórmula para el momento de inercia, podemos calcular el momento de inercia del rectángulo de la siguiente manera:
I = (b * h ^ 3) / 12
I = (2 * 4^ 3) / 12
I = (2 * 64) / 12
= 10.67 in^4
Entonces el momento de inercia del rectángulo es 10.67 pulgadas^4. Este momento de inercia es sobre el eje centroidal, recuerda que si necesitas encontrar el momento de inercia sobre un eje diferente, necesitará usar una fórmula diferente o realizar una transformación. También puede verificar que la unidad sea siempre el producto de la potencia de la unidad de entrada, en este caso todas las unidades de entrada son pulgadas, por lo que el resultado es en pulgadas ^ 4.
Podemos verificar este resultado con la calculadora gratuita de momento de inercia, que muestra el mismo resultado de 10.6667 in^4:
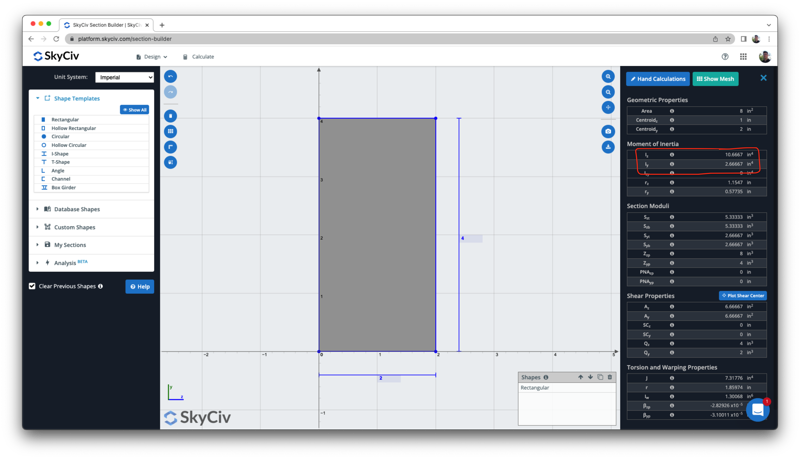
Cómo encontrar el momento de inercia - Viga en I
Ahora veamos un caso más complejo donde la sección transversal es una viga I, con diferentes dimensiones. El concepto es el mismo, sin embargo, el enfoque en este caso es bastante diferente. Básicamente, necesitamos ver la viga I como una combinación de diferentes rectángulos y sumar las diferentes partes para obtener el Momento de inercia completo de la sección. En resumen, tenemos que seguir estos tres pasos:
- Calcular el Eje Neutro para toda la sección
- Calcular el MOI de cada parte
- Calcular el momento de inercia usando el teorema de los ejes paralelos - que es esencialmente la suma de los momentos de inercia individuales
Así que consideremos la siguiente sección:
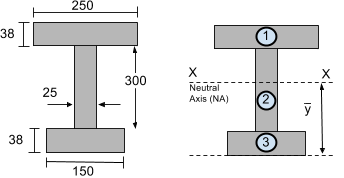
El eje neutral (EN) se encuentra en el centroide. Esto es esencialmente un promedio ponderado del área y la distancia desde el fondo para cada segmento. Simplemente necesitamos usar la ecuación del centroide para calcular la vertical (y) centroide de una forma de múltiples segmentos.

Tomaremos el datum o línea de referencia desde la parte inferior de la sección de la viga. Ahora encontremos Ai y yi para cada segmento de la sección de viga I que se muestra arriba para que se pueda encontrar el centroide vertical o y.


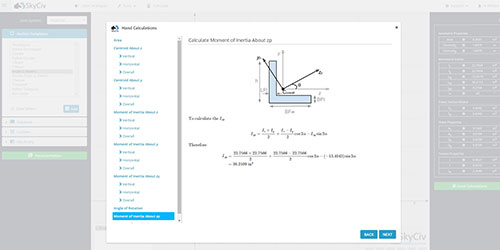
Ahora tenemos el centroide. Podemos seguir calculando el momento de inercia. Para calcular el momento total de inercia de la sección, necesitamos usar el "Teorema del Eje Paralelo" Como es definido debajo:

Como lo hemos dividido en tres partes rectangulares, debemos calcular el momento de inercia de cada una de estas secciones. Ahora podemos usar la fórmula simplificada del momento de inercia rectangular:
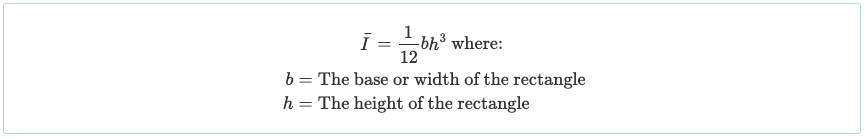
Ahora tenemos toda la información que necesitamos para usar el "Teorema del Eje Paralelo" y encontrar el momento total de inercia de la sección de viga en I. En nuestro momento de inercia ejemplo:

Una vez más, podemos comparar este resultado con el de la calculadora gratis de momento de inercia para comparar los resultados tanto del centroide como del momento de inercia, donde tanto el centroide (216.29 in) y momento de inercia (4.74 x 10 ^ 8 pulgadas ^ 4) concuerdan:
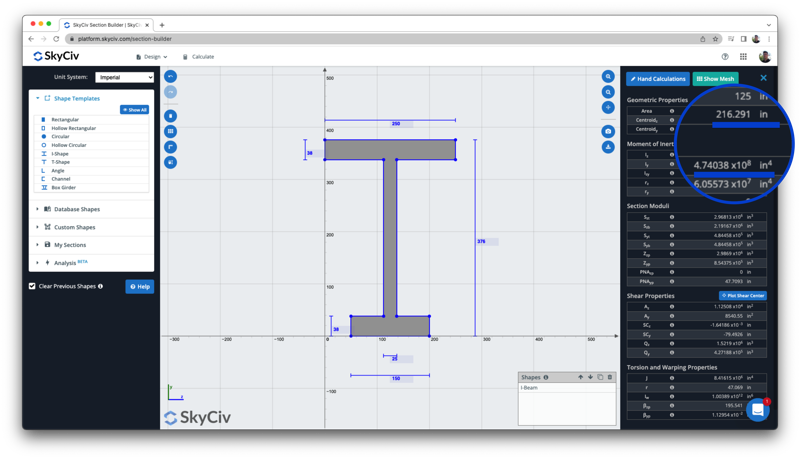
Ecuaciones de momento de inercia
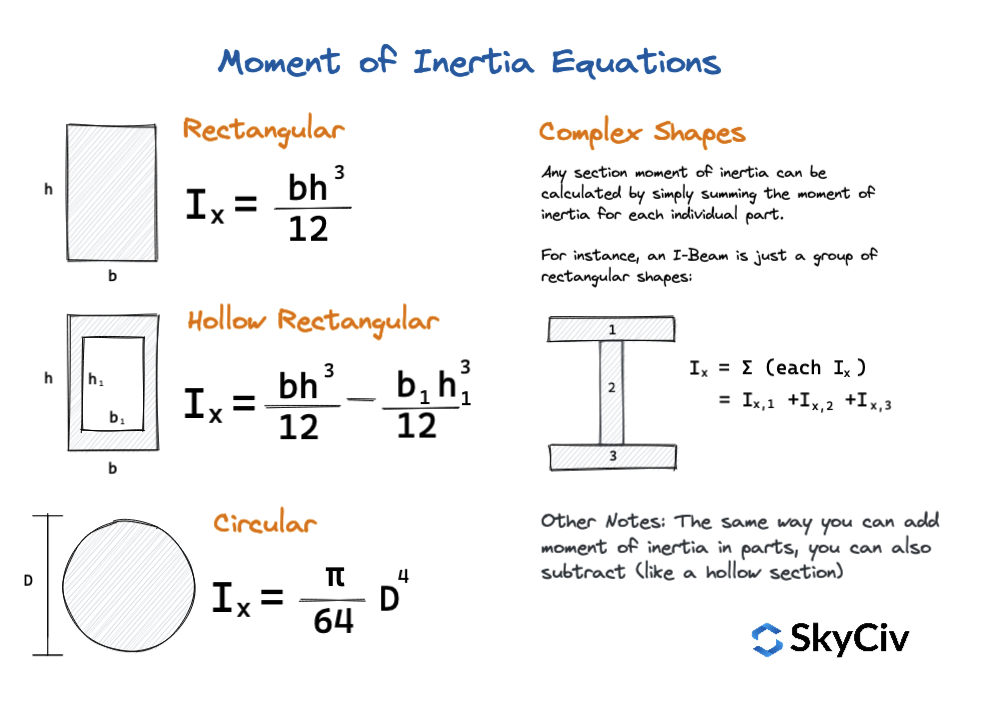
También se pueden usar ecuaciones simples para calcular el momento de inercia de formas y secciones comunes.. Estas son ecuaciones rápidas de momento de inercia que proporcionan valores rápidos y son una excelente manera de contrastar o verificar dos veces sus resultados.. Centrándonos solo en formas simples, el siguiente diagrama muestra algunas de estas ecuaciones:
Calculador de Centroides de SkyCiv
Un centroide, también conocido como el 'centro geométrico', es el centro de masa de un objeto con densidad uniforme. Una demostración simplificada de un centroide, sería el lugar en el que necesitaría colocar un lápiz para que se equilibre en su dedo. La ubicación en la que el lápiz se equilibra y no se cae de su dedo sería la ubicación aproximada del centroide del lápiz.. Considera la masa y la densidad del material para determinar el punto donde la masa del lápiz es igual en ambos lados de tu dedo, y por lo tanto representa el 'centro de masa' del lápiz.
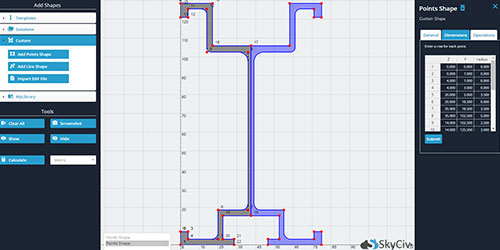
La calculadora SkyCiv Centroid utiliza FEA para proporcionar resultados altamente precisos en segundos, no importa cuán compleja sea la forma. En la versión premium, los usuarios pueden ingresar las coordenadas de los puntos que definen la forma y nuestra calculadora le dará las coordenadas del centroide. Esto incluye la capacidad de diseñar formas personalizadas a través de la importación de DXF, múltiple (construido) formas y formas de puntos personalizadas.
Además de su velocidad y precisión, nuestra calculadora de centroide también es increíblemente fácil de usar. Con una interfaz de usuario sencilla, puede ingresar las dimensiones de su sección y recibir los valores de propiedad de su sección (incluyendo el centroide de la sección de la viga) en segundos. Ya sea que esté trabajando en un proyecto de diseño, experimentando con diferentes secciones o estudiando para un examen, SkyCiv Centroid Calculator es la herramienta perfecta para ayudarlo a hacer el trabajo.
Calculadora de Módulo de Sección
Como se mencionó anteriormente, esta herramienta gratuita también le proporciona un cálculo del módulo de sección elástica, sin embargo, si está comenzando como ingeniero, es posible que no entienda qué es el módulo de sección. Para hacerlo mas simple, el módulo de sección es una propiedad de sección de una sección transversal que mide la resistencia a la flexión y se calcula como la relación entre el momento de inercia y la distancia desde el eje neutro hasta la fibra más distante. El módulo de sección elástica se representa en esta ecuación simplemente como:
Dónde,
- S es el módulo de sección
- I es el momento de inercia de la sección respecto al eje neutro
- y es la distancia desde el eje neutro hasta el punto más alejado de la sección
Hay dos tipos de módulo de sección: Elástico y Plástico. En América, S se usa típicamente para referirse al módulo de sección elástica, mientras que Z se usa para referirse al módulo de sección plástica. En Gran Bretaña y Australia, estos son típicamente invertidos. El módulo de sección elástica se suele denominar con una letra Z, mientras que el Módulo de Sección Plástica se denomina con una letra S.
En general, el módulo de sección elástica se usa para el diseño de secciones porque es aplicable hasta el límite elástico para la mayoría de los metales. Los metales no suelen estar diseñados para ir más allá del límite elástico del material..
Documentación adicional
Consulte las siguientes páginas de documentación para obtener información más detallada sobre el momento de inercia, cómo calcularlos para varias formas, y cómo usar nuestra calculadora de centroide:
Más Herramientas Gratuitas Disponibles
SkyCiv también ofrece otras herramientas como la herramienta de tamaño de viga I y el software gratuito de diseño estructural. El parte de Sección Dinámica también te mostrará una representación gráfica de tu sección de viga. Entonces, si quieres calcular el momento de inercia del círculo, rectángulo o cualquier otra forma, no dudes en utilizar el siguiente software o nuestro SkyCiv Constructor de Sección con todo incluido.
SkyCiv ofrece una amplia gama de Software de Análisis y Diseño Estructural en la Nube para ingenieros. Como una empresa tecnológica en constante evolución, estamos comprometidos con la innovación y desafiando los flujos de trabajo existentes para ahorrar tiempo a los ingenieros en sus procesos de trabajo y diseños.
Necesitas más Funcionalidades?
Actualiza a un plan plan profesional para desbloquear funciones completas