El momento de inercia es una propiedad geométrica importante utilizada en ingeniería estructural.. Está directamente relacionado con la cantidad de resistencia del material que tiene su sección.. Generalmente, un mayor momento de inercia implica una mayor resistencia en la sección, lo que resulta en una deflexión reducida cuando se somete a una carga. El momento de inercia de un rectángulo., o cualquier forma para el caso, es técnicamente una medida de cuánto torque se requiere para acelerar la masa alrededor de un eje – de ahí la palabra inercia en su nombre.

Fórmula del momento de inercia de un rectángulo

La fórmula general utilizada para determinar cómo encontrar el momento de inercia de un rectángulo es:

[math] YO_{xx}= dfrac{BD^3}{12} , YO_{aa}= dfrac{B^3D}{12} [math]

Donde el xx y aa referirse al eje particular, o dirección, siendo considerado.

Es una convención común de ingeniería estructural que B se refiere a anchura del rectángulo, paralelo a un convencionalmente horizontal eje x.

De igual forma, re se refiere a profundidad del rectángulo, paralelo a un convencionalmente vertical y-axis.

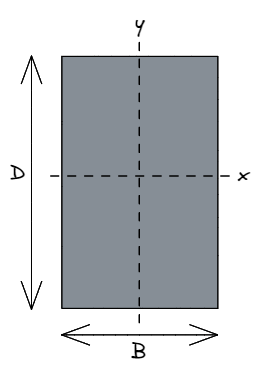
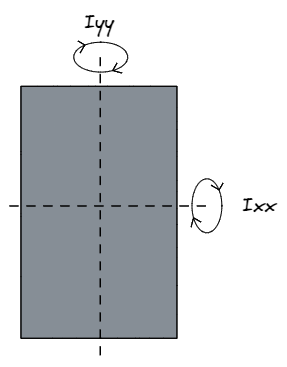
Puede ser confuso al principio, pero cuando los ingenieros estructurales se refieren a IXX de hecho, están haciendo referencia a la fuerza de una sección. sobre el eje x, es decir, en una dirección paralela a la re dimensión, o eje y. De igual forma, Yyy se refiere a la fuerza sobre el eje y, es decir, en una dirección paralela a la B dimensión, o eje x.

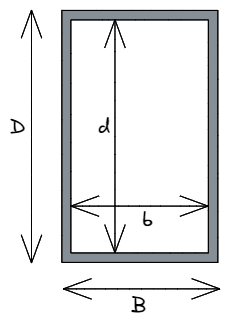
Secciones huecas rectangulares (RHS)

Mientras que los ingenieros hipotéticamente podrían usar secciones rectangulares sólidas al diseñar, esto usaría una cantidad significativamente mayor de materia prima, con los correspondientes aumentos de peso y coste. Es mucho más común usar rectangular secciones huecas (comúnmente conocido como un RHS). Aquí podemos utilizar la misma ecuación definida anteriormente para el caso rectangular general, sin embargo, debemos restar el interior hueco área del rectángulo:

[math] YO_{xx}= dfrac{BD^3}{12} – \dfrac{bd ^ 3}{12} [math]

En este caso, minúsculas b y re denota el tamaño del área hueca dentro del rectángulo que debemos restar de las dimensiones exteriores de la forma, estar en mayúsculas B y re. La diferencia entre cada dimensión correspondiente se refiere al espesor del material en esa dimensión – es decir. B – b = espesor total del material paralelo al eje x.

Además de los claros ejemplos de peso y uso de materiales, ¿Por qué las secciones huecas a menudo se describen como más eficiente que sus contrapartes sólidas?

Considere una viga sometida a una carga vertical hacia abajo. Esperamos que las fibras superiores del material experimenten una fuerza de compresión., mientras que las fibras inferiores correspondientes sufrirán una fuerza de tracción. Las fibras a lo largo del eje neutro de la sección (paralela al baricentro de la sección) sin embargo, no experimentará compresión ni tensión, de ahí el nombre neutral eje.

En tono rimbombante, la magnitud de estas fuerzas de compresión o tracción dependen de la distancia desde este eje neutral – material cerca al eje neutro necesita resistir Menos fuerza.

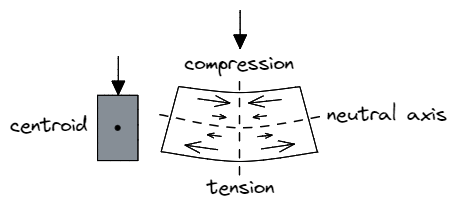
Como tal, El material interno de una sección completamente sólida resiste una cantidad de fuerza relativamente pequeña mientras ocupa una cantidad de área relativamente grande porque el material más externo trabaja más duro.! Quitando esta parte interior de la sección y haciéndola hueca en consecuencia mejora la eficiencia de la sección con respecto a su peso, costo, y uso de materiales.

Conclusión

En resumen, la fórmula para determinar el momento de inercia de un rectángulo es Ixx=BD³ ⁄ 12, Iyy=B³D ⁄ 12. Para secciones huecas rectangulares, la fórmula es Ixx=BD³ ⁄ 12 – bd³ ⁄ 12.

La inercia del momento es importante tanto para la fuerza/esfuerzo del momento de flexión como para la deflexión.. Esto es evidente en sus fórmulas., como en ambos casos, I (Momento de Inercia) esta en el denominador:

Fuente: Fórmula de tensión de flexión

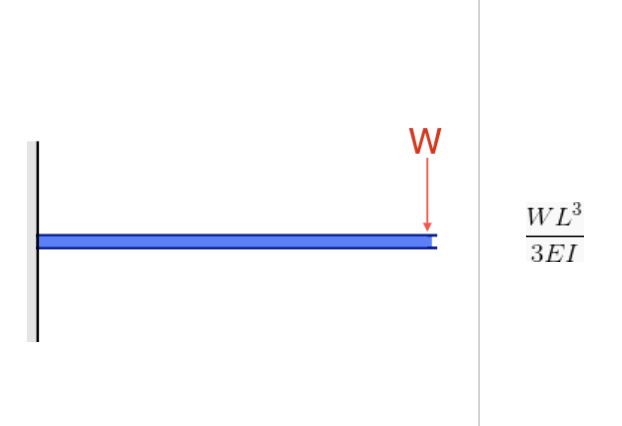
Fuente: Ecuación de la deflexión en una viga en voladizo

Calculadora de momento de inercia de un círculo

Si quieres calcular el momento de inercia, echa un vistazo a nuestro tutorial sobre el Momento de inercia de un círculo para ver cómo las formas de sección circular y rectangular se comparan entre sí.

Calculadora gratis de Momento Inercia