Cómo calcular las fuerzas axiales de un sistema de armadura utilizando el método de articulaciones?
En este tutorial, explicaremos cómo usar el método de las juntas para calcular las fuerzas internas de los miembros en un sistema o estructura de truss.
Estas fuerzas se conocen como Fuerzas Axiales y son muy importantes en el análisis de armaduras.. Si no está seguro de lo que se ve un braguero en nuestro artículo – ¿Qué es un braguero?. El método de las articulaciones consiste básicamente en observar cada una de las articulaciones ‘’ (donde los miembros se encuentran) y aplicando ecuaciones estáticas para resolver.
la gran cosa es, Armadura SkyCiv hace esto automáticamente por ti. Modele sus propios trusses y el software le mostrará paso a paso de forma interactiva el método de las uniones!
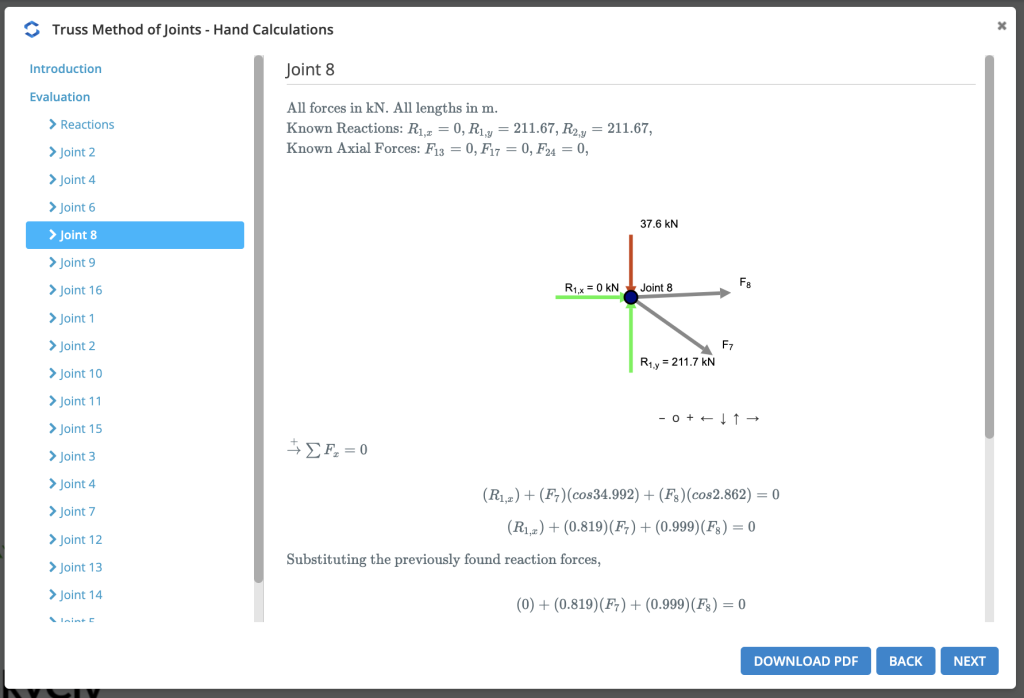
Paso 1: Calcule las reacciones en los soportes
primero, calculamos el reacciones en los apoyos. Comenzaremos mirando un ejemplo simple de un 5 sistema de braguero miembro:
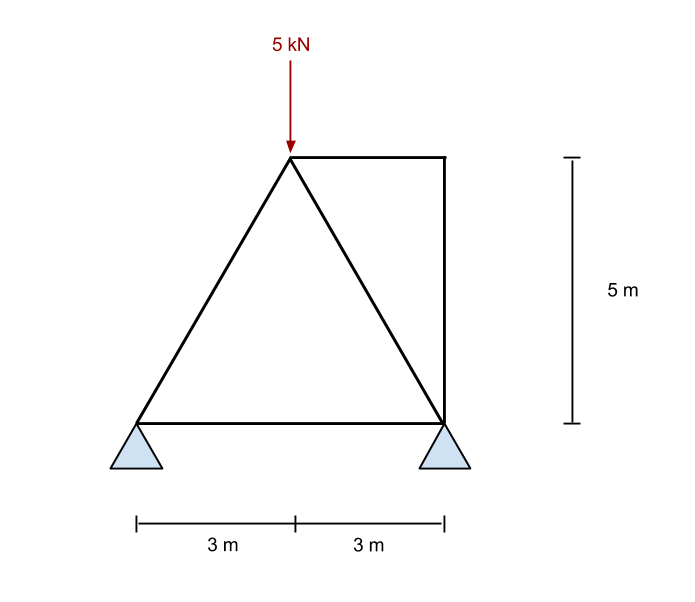
Para calcular el momento flector en este sistema de vigas, primero tomamos la suma de momentos en la reacción de la izquierda como cero. Hacemos esto ignorando a todos los miembros y simplemente mirando las fuerzas y apoyos en la estructura.. Es el mismo que el método utilizado en las reacciones del momento flector en nuestro tutorial anterior..
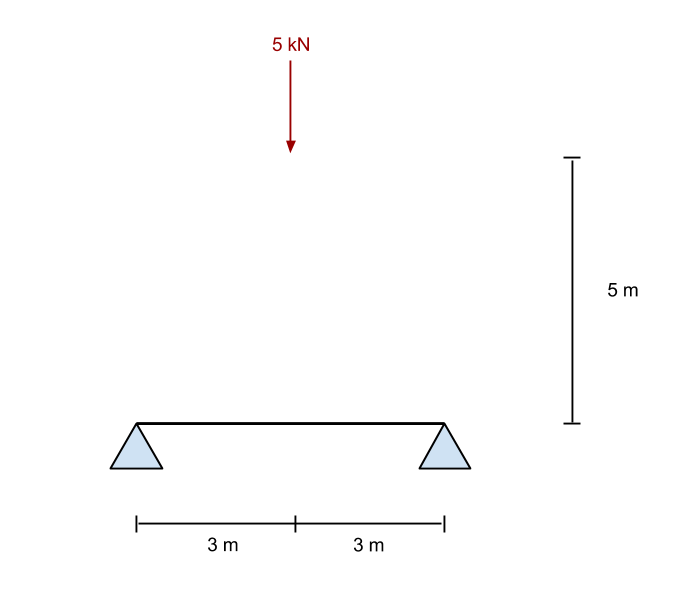
De las ecuaciones anteriores, resolvemos la fuerza de reacción en el punto B (el soporte adecuado). En nuestro ejemplo, esto funciona para ser 2.5 kN en una dirección ascendente. Ahora, si tomamos la suma de las fuerzas en el y (vertical) dirección, encontramos ese soporte A (el soporte izquierdo) también se da como 2.5 kN.
Paso 2: Considere uno de los soportes:
Ahora que tenemos las fuerzas de reacción, podemos comenzar el análisis del resto de esta estructura de celosía.. En primer lugar, miramos a una de nuestras fuerzas conocidas – en este caso, consideraremos la reacción de soporte izquierdo de +2.5 kN. Como sabemos que esta fuerza ocurre en este punto, consideraremos solo este punto de forma aislada. Repetimos este proceso varias veces, Por lo tanto, es importante practicar y aprender el proceso para tener una buena comprensión de cómo resolver las fuerzas axiales en estructuras de armadura. Así que de nuevo, considerar el primer punto en el soporte:
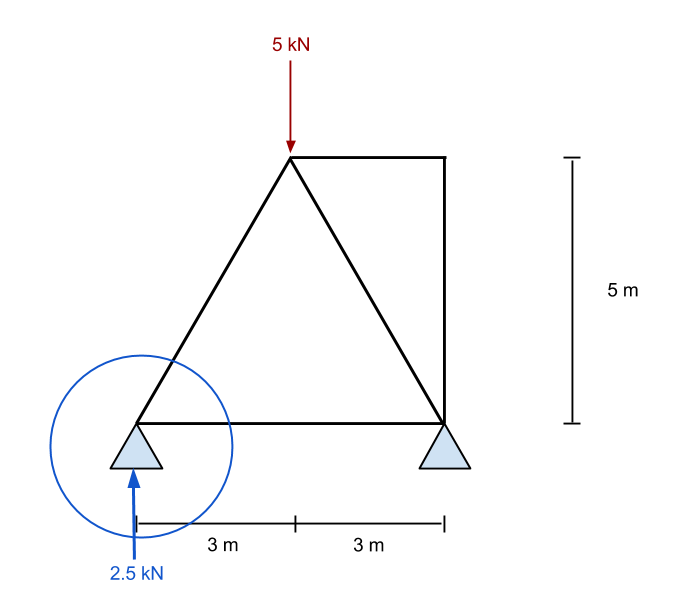
Zoom en este punto, vemos todas las fuerzas conocidas actuando en este punto. De la estática, sabemos que las fuerzas en la dirección x e y ambas deben sumar cero. En consecuencia, si sabemos que hay una fuerza vertical hacia arriba, entonces debe haber una fuerza hacia abajo para contrarrestarlo. Como ya tenemos el valor de una fuerza que mira hacia arriba, entonces intentaremos evaluar el número de miembro 1 primero.
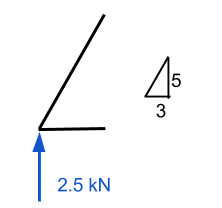
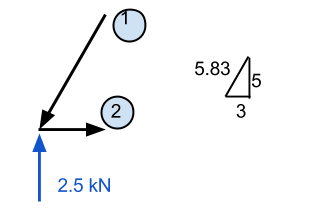
Aquí requerimos algunos conocimientos de vectores. Es importante recordar que todas las fuerzas deben sumar cero para las direcciones x e y. En nuestro ejemplo, la distancia horizontal es de 3 m mientras que la vertical es de 5 m – dejándonos con la hipotenusa igual a aproximadamente 5.83 m. Usando esto, podemos deducir que el componente de fuerza normal del miembro 1 es igual a (5.83)/(5) veces la fuerza vertical de 2.5 kN. Esto equivale a 2.92 kN y DEBE ser una fuerza que actúe hacia abajo si el punto debe permanecer estacionario.
Miembro 2 se puede calcular de la misma manera. Si conocemos a ese miembro 1 está actuando hacia abajo, entonces sabemos que también debe actuar a la izquierda. En consecuencia, sabemos miembro 2 debe generar una fuerza que empuja el punto hacia la derecha para mantener las fuerzas en la dirección x. Este valor se calcula mediante (3/5.83) x 2.92 kN y es igual a 1.51 kN.
Paso 3: Moverse a otro punto:
Habiendo calculado las fuerzas internas del primer miembro en nuestro truss, ahora veremos otro punto para repetir el proceso:
De nuevo, nos acercaremos al punto de referencia y consideraremos todas las fuerzas conocidas que actúan sobre el punto:
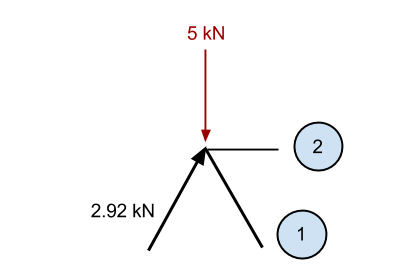
De la misma manera que antes, si sumamos el componente vertical conocido de la 2.92 miembro de kN (2.5 kN en dirección vertical) y el – 5kN fuerza hacia abajo, entonces tenemos un exceso en la dirección hacia abajo de 2.5 kN (5 – 2.5). En consecuencia, conocemos a ese miembro 1 debe estar causando una fuerza hacia arriba para mantener el punto estático. Esta fuerza debe tener un componente vertical de 2.5 kN, y dado que está en el mismo ángulo que el miembro anterior, entonces la fuerza axial interna también debe ser 2.92 kN.
Ahora consideramos las fuerzas en la dirección x. En este punto, toda la fuerza vertical del miembro 1 está resistiendo la fuerza vertical del miembro previamente calculado. Esto significa que la suma de fuerzas en la dirección x ya es cero. En consecuencia, no puede haber fuerza en miembro 2 o de lo contrario el punto se volverá desequilibrado y ya no será estático.
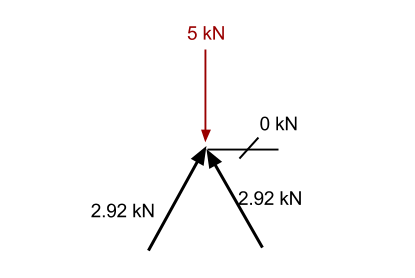
Paso 4: Moverse a otro punto:
Mirando este punto, podemos ver que hay un caso especial. En esta situación, cualquier fuerza que empuje hacia arriba no tendrá acción de resistencia posible, ya que no hay otro miembro que pueda proporcionar una fuerza hacia abajo para mantener el punto estático. En consecuencia, ya que la suma de fuerzas debe ser cero, ese miembro no puede tener ninguna fuerza asociada. Eso, por lo tanto, no tiene fuerza y es conocido como un miembro cero.
De nuevo, si nos fijamos en sumar las fuerzas en la dirección x, podemos ver que solo hay un miembro que tiene alguna fuerza en la dirección x. En consecuencia, esto también debe tener 0 fuerza axial para que la suma de fuerzas sea igual a cero.

Solución final
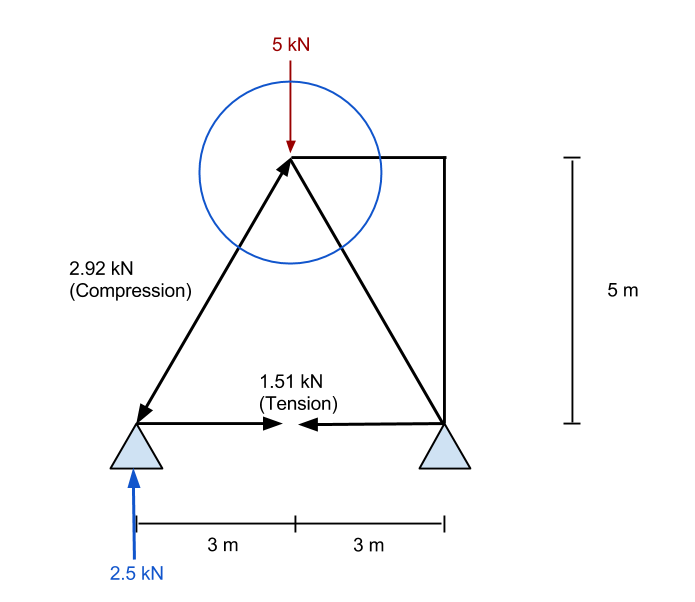
Finalmente, terminamos con el siguiente resultado para nuestro braguero. Podemos ver todas las fuerzas axiales resultantes dentro del miembro y el reacciones en los apoyos. El siguiente resultado fue tomado de nuestro Calculadora de braguero gratis – darle una oportunidad, es gratis!
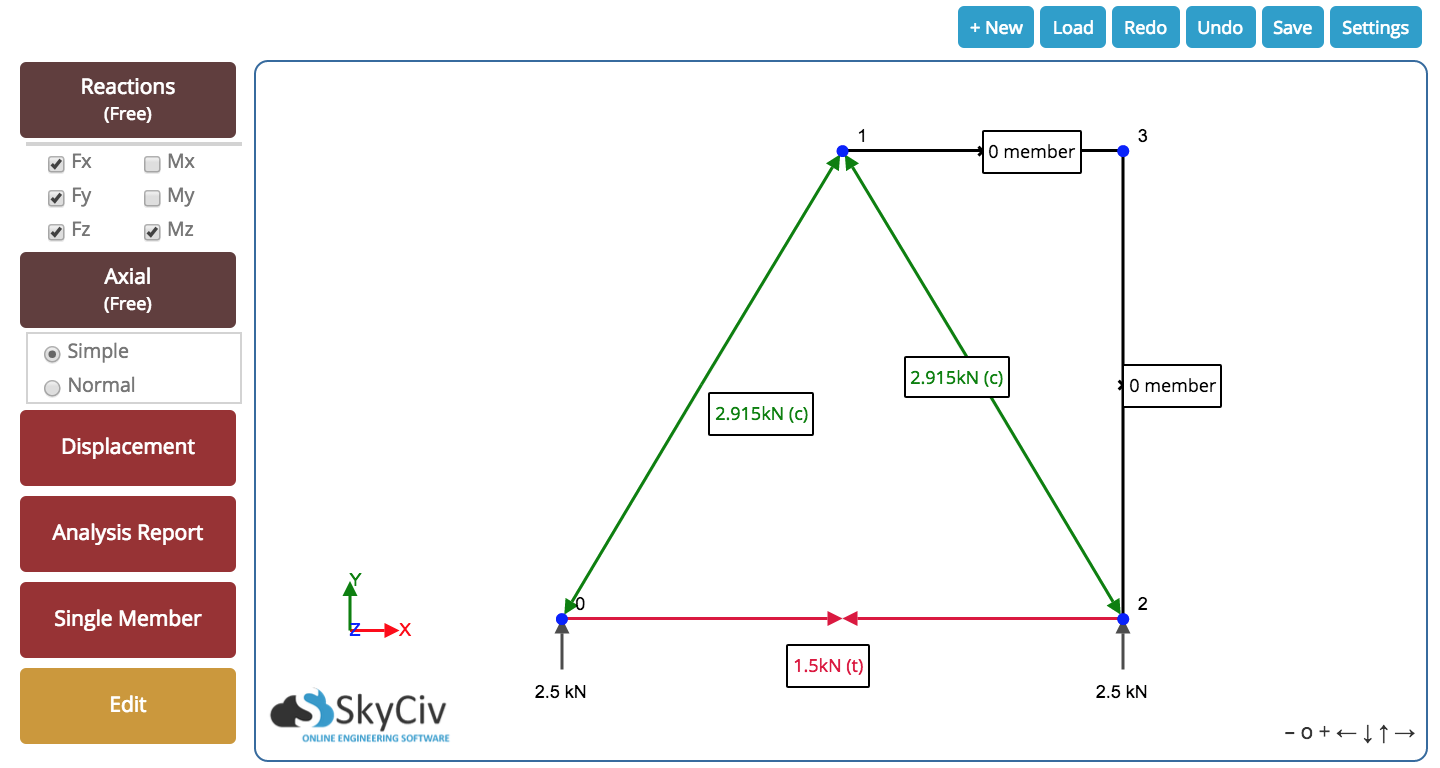
Pasos sencillos
- Comience siempre calculando las reacciones en los soportes
- Elija un punto con una fuerza conocida y mírelo de forma aislada
- Usa geometría vectorial y la suma de fuerzas = 0 para resolver las otras fuerzas miembro
- Repita el proceso hasta que todos los miembros estén resueltos.
- Recuerde estar atento a los Miembros Cero
Tutoría relevante
- Resolviendo truss por el método de las secciones. Incluye un video y una guía paso a paso.
Armadura SkyCiv
Armadura SkyCiv puede calcular el método de las articulaciones automáticamente para usted. O prueba nuestro Calculadora de braguero gratis que te dará la respuesta final (sin cálculos manuales).
Para explorar más funciones del software SkyCiv, Regístrese hoy para comenzar!

