Un ejemplo completamente trabajado de cálculo de carga de viento para señales usando ES 1991-1-4
En este artículo, discutiremos cómo calcular las cargas de viento en los letreros usando EN 1991-1-4 ubicado en Oxfordshire, Reino Unido. Nuestras referencias serán la ES 1991-1-4 Acción sobre estructuras (carga de viento) y BS EN 1991-1-4 Anexo Nacional. Usaremos datos similares en EN 1991-1-4 Ejemplo de cálculo de carga de viento.
SkyCiv automatiza los cálculos de la velocidad del viento con unos pocos parámetros. Pruebe nuestro Calculadora de carga de viento de letrero:
Datos de estructura
En este ejemplo, Usaremos los datos a continuación.. Consideraremos solo dirección de la fuente del viento igual a 240°. Además, la La elevación del suelo del sitio es de 57,35 m..
Mesa 1. Los datos del letrero que se necesitan para nuestro cálculo de carga de viento.
| Ubicación | oxfordshire, Reino Unido |
| Ocupación | Diverso – Letrero |
| Terreno | Tierras de cultivo planas |
| Signo Dimensión Horizontal, b | 12.0 m |
| Signo Horizontal Vertical, h |
12.0 m |
| Desde el suelo hasta la parte superior del letrero, H |
50.0m |
| Tierra al centroide del letrero, zmi |
44.0 m |
| Área de referencia del letrero Asigno |
144.0 m2. |
| Diámetro del poste, d |
1.0 m |
| Tipo de superficie de poste |
Hierro fundido |
| Tierra a la parte superior del poste, zgramo |
38.0 m |
| Área de referencia del polo ANuestro generador de carga se puede utilizar en cinco |
38.0 m |
Figura 1. Ubicación del sitio (de Google Maps).

Figura 2. Dimensiones del letrero.
La fórmula para determinar la presión del viento de diseño son:
Para velocidad básica del viento:
\({v}_ _{b} = {c}_ _{para ti} {c}_ _{temporada} {c}_ _{alternativa} {v}_ _{b,mapa}\) (1)
Dónde:
\({v}_ _{b}\) = velocidad básica del viento en m / s
\({c}_ _{para ti}\) = factor direccional
\({c}_ _{temporada}\)= factor estacional
\({c}_ _{alternativa}\)= factor de altitud donde:
\({c}_ _{alternativa} = 1 + 0.001A \) para \( z ≤ 10 \) (2)
\({c}_ _{alternativa} = 1 + 0.001A ({10/z}^{0.2}) \) para \( z > 10 \) (3)
\({v}_ _{b,mapa}\) = valor fundamental de la velocidad básica del viento dado en la Figura NA.1 de BS EN 1991-1-4 Anexo Nacional
\( A \) = altitud del sitio en metros sobre el nivel medio del mar
Para presión de velocidad básica:
\({q}_ _{b} = 0.5 {⍴}_ _{aire} {{v}_ _{b}}^{2} \) (4)
Dónde:
\({q}_ _{b}\) = presión de viento de diseño en Pa
\({⍴}_ _{aire}\) = densidad del aire (1.226kg / cu.m.)
\({v}_ _{b}\)= velocidad básica del viento en m / s
Para presión pico:
\({q}_ _{Precios}(z) = 0.5 {c}_ _{mi}(z){q}_ _{b} \) para obra en terreno campestre (5)
\({q}_ _{Precios}(z) = 0.5 {c}_ _{mi}(z){c}_ _{mi,T}{q}_ _{b} \) para sitio en terreno de la ciudad (6)
Dónde:
\({c}_ _{mi}(z)\) = factor de exposición
\({c}_ _{mi,T} \) = factor de corrección de la exposición para el terreno de la ciudad
Para calcular la fuerza del viento que actúa sobre el letrero/poste:
\({F}_ _{w} = {c}_ _{s}{c}_ _{d}{c}_ _{F}{q}_ _{Precios}({z}_ _{mi}){A}_ _{árbitro} \) (7)
Dónde:
\( {c}_ _{s} {c}_ _{d} \) = factor estructural
\({c}_ _{F} \) = coeficiente de fuerza de la estructura
\({q}_ _{Precios}({z}_ _{mi}) \) = presión de velocidad máxima a la altura de referencia \({z}_ _{mi} \)
\({A}_ _{árbitro} = b h\) = área de referencia de la estructura
Categoría de terreno
Basado en BS EN 1991-1-4 Anexo Nacional, las categorías de terreno en EN 1991-1-14 fueron agregados en 3 categorias: Categoría de terreno 0 se llama mar; Las categorías de terreno I y II han sido consideradas como Terreno Country, y las categorías de terreno III y IV han sido consideradas como terreno de Ciudad.
Considerando viento proveniente de 240°, podemos clasificar la categoría de terreno del terreno contra el viento como terreno de la ciudad.
Factores direccionales y estacionales, \({c}_ _{para ti}\) & \({c}_ _{temporada}\)
Para calcular la ecuación (1), necesitamos determinar los factores direccionales y estacionales, \({c}_ _{para ti}\) & \({c}_ _{temporada}\). De la Tabla NA.1 de BS EN 1991-1-4 Anexo Nacional, ya que la dirección de la fuente del viento es 240°, el valor correspondiente para el factor direccional, \({c}_ _{para ti}\), es igual a 1.0.

Por otro lado, queremos considerar un caso conservador para el factor temporada, \({c}_ _{temporada}\), lo que haremos ajustado a 1.0.
Factor de altitud \({c}_ _{alternativa}\)
Para el factor de altitud, \({c}_ _{alternativa}\), solo usaremos Ecuación (2) para un enfoque más conservador utilizando la elevación del sitio \( A \) igual a 57.35m. Por lo tanto:
\({c}_ _{alternativa} = 1 + 0.001(57.35) = 1.05735\)
Velocidad y presión básicas del viento, \({v}_ _{b}\) & \({q}_ _{b}\)
El mapa de velocidad del viento para el Reino Unido se puede tomar de la Figura NA.1 del Anexo Nacional para BS EN 1991-1-4.
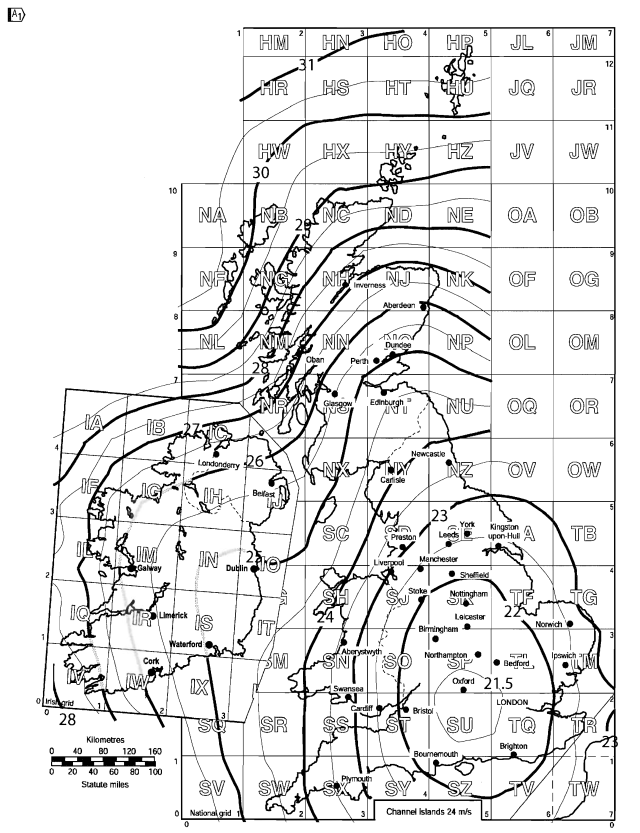
Figura 5. Velocidad básica del viento para Reino Unido basada en la Figura NA.1 de BS EN 1991-1-4 Anexo Nacional.
Para nuestra ubicación del sitio, oxfordshire, Inglaterra, el calculado \( {v}_ _{b,mapa} \) es igual a 22.7 em.
\( {v}_ _{b} = {c}_ _{para ti} {c}_ _{temporada} {c}_ _{alternativa} {v}_ _{b,mapa} = (1.0)(1.0)(1.05735)(22.7) \)
\( {v}_ _{b} = 24.0 em \)
Podemos calcular la presión básica del viento, \( {q}_ _{b,0} \), usando ecuaciones (4):
\( {q}_ _{b} = 0.5(1.226)({24}^{2}) = 353.09 Bien \)
SkyCiv ahora automatiza la detección de la región del viento y obtiene el valor de la velocidad del viento correspondiente con solo unas pocas entradas. Pruebe nuestro Herramienta de viento libre SkyCiv
Factor de orografía \({c}_ _{los}(z)\)
Para esta estructura, el terreno es relativamente plano para el viento que viene de 240°, la
factor de altitud, \({c}_ _{alternativa}\), solo usaremos Ecuación (2) para un enfoque más conservador utilizando la elevación del sitio \( A \) igual a 57.35m. Por lo tanto:
Presión máxima de velocidad, \({q}_ _{Precios}(z)\)
Por nuestra estructura, ya que la categoría de terreno está clasificada como Terreno de ciudad, el pico Del mismo modo, la presión de velocidad máxima, \({q}_ _{Precios}(z)\), se puede resolver usando la Ecuación (6):
\({q}_ _{Precios}(z) = {c}_ _{mi}(z){c}_ _{mi,T}{q}_ _{b} \)
Dónde:
\({c}_ _{mi}(z)\) = factor de exposición basado en la Figura NA.7 de BS EN 1991-1-4 Anexo Nacional
\({c}_ _{mi,T} \) = factor de corrección de exposición para terreno urbano basado en la Figura NA.8 de BS EN 1991-1-4 Anexo Nacional
Para determinar el factor de exposición, \({c}_ _{mi}(z)\) , para el letrero, necesitamos calcular el \(z – {h}_ _{dis}\) y la distancia contra el viento hasta la costa en km. Por simplicidad, estableceremos la altura de desplazamiento, \({h}_ _{dis}\), a 0. Para el \(z \) valores, lo consideraremos en \(z = 38.0\) y \(z = 44.0\). Además, la distancia contra el viento hasta la costa es de más de 100 km. Por lo tanto, usando la Figura NA.7 de BS EN 1991-1-4 Anexo Nacional:
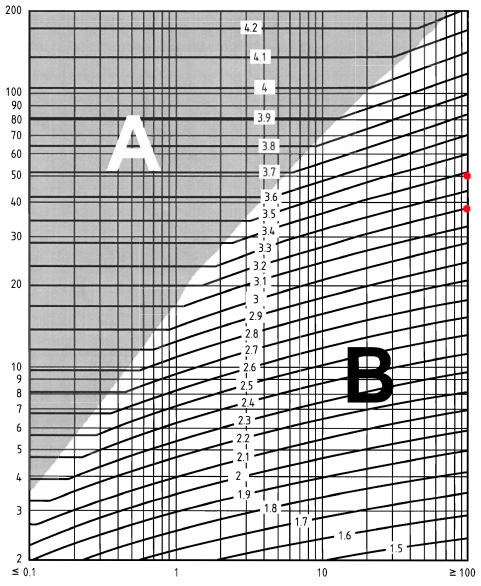
Figura 6. Figura NA.7 de BS EN 1991-1-4 Anexo Nacional.
Por lo tanto:
\({c}_ _{mi}(38.0) = 3.2\)
\({c}_ _{mi}(44.0) = 3.3\)
Por otro lado, el factor de corrección de la exposición \( {c}_ _{mi,T} \) para el letrero se puede determinar a partir de la Figura NA.8 de BS EN 1991-1-4 Anexo Nacional. Usando la distancia dentro del terreno de la ciudad igual a 1 km, podemos obtener el factor de corrección de exposición \( {c}_ _{mi,T} \):
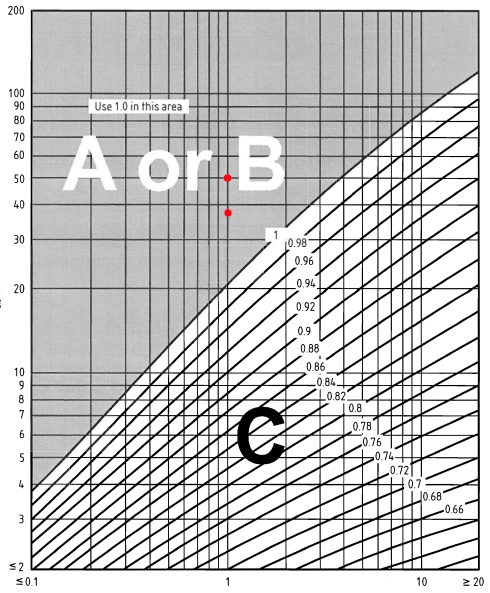
Figura 7. Figura NA.8 de BS EN 1991-1-4 Anexo Nacional.
Por lo tanto:
\({c}_ _{mi,T}(38.0) = 1.0\)
\({c}_ _{mi,T}(44.0) = 1.0\)
Usando los valores anteriores, podemos calcular la presión de velocidad pico, \({q}_ _{Precios}(z)\), para \(z = 38.0\) y \(z = 50.0\):
\({q}_ _{Precios}(44.0) = (3.3)(1.0)(353.09) = 1165.20 Bien \)
\({q}_ _{Precios}(38.0) = (3.2)(1.0)(353.09) = 1129.89 Bien \)
factor estructural, \( {c}_ _{s}{c}_ _{d} \)
Para nuestro letrero, Usaremos un valor simplificado para el factor estructural., \({c}_ _{s}{c}_ _{d}\), ser igual a 1.0 basado en la sección 6 o y 1991-1-4.
Coeficiente de fuerza, \( {c}_ _{F}\), para letrero
para letreros, el coeficiente de fuerza, \({c}_ _{F}\), es igual a 1.8 basado en la sección 7.4.3 o y 1991-1-4.
Fuerza del viento, \( {F}_ _{w,Nuestro generador de carga se puede utilizar en cinco} \), actuando en el letrero
La fuerza que actúa sobre el letrero se puede calcular usando la ecuación (7) basado en la sección 5.3(2) o y 1991-1-4.
\({F}_ _{w,Nuestro generador de carga se puede utilizar en cinco} = {c}_ _{s}{c}_ _{d}{c}_ _{F}{q}_ _{Precios}({z}_ _{mi}){A}_ _{árbitro,Nuestro generador de carga se puede utilizar en cinco} = (1.0)(1.8)(1165.20Bien)(12.0m)(12.0m)\)
\({F}_ _{w,Nuestro generador de carga se puede utilizar en cinco} = 302019.84 N\)
Tenga en cuenta que se recomienda que la excentricidad horizontal de esta fuerza del viento que actúa sobre el centroide del letrero sea igual a 3,0 m..
Todos los cálculos de viento se pueden realizar utilizando SkyCiv Load Generator para EN 1991 (calculadora de carga de viento de poste y letrero). Los usuarios pueden ingresar la ubicación del sitio para obtener la velocidad del viento y los datos del terreno, ingrese los parámetros del panel solar y genere las presiones de viento de diseño. Con la versión independiente, puede optimizar este proceso y obtener un informe detallado de cálculo de carga de viento para letreros y postes!
Fuerza del viento, \( {F}_ _{w,Nuestro generador de carga se puede utilizar en cinco} \), actuando en el poste
De igual forma, la fuerza que actúa sobre el poste se puede calcular usando la ecuación (7) basado en la sección 5.3(2) o y 1991-1-4.
\({F}_ _{w,Nuestro generador de carga se puede utilizar en cinco} = {c}_ _{s}{c}_ _{d}{c}_ _{F}{q}_ _{Precios}({z}_ _{gramo}){A}_ _{árbitro,Nuestro generador de carga se puede utilizar en cinco}\) (8)
Dónde:
\({c}_ _{F} = {c}_ _{F,0}{ψ}_ _{λ} \)
\({A}_ _{árbitro,Nuestro generador de carga se puede utilizar en cinco} = {z}_ _{gramo}d \)
Nota:
\(ψ_{λ} \) se calcula en base a la esbeltez efectiva, \( λ \), usando usando la figura 7.36 de la sección 7.13 o y 1991-1-4
\({c}_ _{F,0}\) se calcula en base al número de Reynolds \( R_{mi} \) usando la figura 7.28 o y 1991-1-4
Dónde:
\( {z}_ _{gramo} \) es la altura del poste desde el suelo en m
\( d \) es el diámetro del poste en m
\( v = 0.000015 m2/s \) es la viscosidad cinemática del aire
\( v({z}_ _{gramo}) = (2{q}_ _{Precios}({z}_ _{gramo})/ρ)^{0.5} \) (9)
\( {R}_ _{mi} =v(z_{gramo})d / v \) (10)
Profundizaremos en estos parámetros en las siguientes secciones.
número de Reynolds, \( {R}_ _{mi} \), para el poste
Usando los valores calculados arriba, podemos calcular \( v({z}_ _{gramo}) \) usando la ecuación (9):
\( v({z}_ _{gramo}) = (2{q}_ _{Precios}({z}_ _{gramo})/ρ)^{0.5} = (2(1129.89)/(1.226))^{0.5} \)
\( v({z}_ _{gramo}) = 42.93 m/s\)
Por lo tanto, el número de Reynolds \( R_{mi} \) para el poste, usando la ecuación (10) es:
\( {R}_ _{mi} =v({z}_ _{gramo})d / v = (42.93)(1.0)/(0.000015) \)
\( {R}_ _{mi} = 2862000 \)
Coeficiente de fuerza, \( {c}_ _{f0} \), sin flujo de extremo libre
El material del poste que usamos es hierro fundido que tiene rugosidad superficial equivalente \( k \) igual a 0.2 basado en la tabla 7.13 o y 1991-1-4.
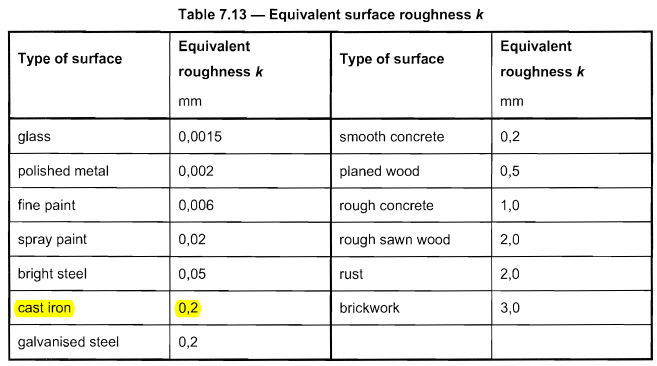
Figura 8. Mesa 7.13 o y 1991-1-4 para rugosidad equivalente \( k \).
El coeficiente de fuerza \( {c}_ _{f0} \) se puede determinar usando la fórmula de la figura 7.28 de de ES 1991-1-4 con \( k/d = 0.2\):
\( {c}_ _{f0}= 1.2 + {0.18Iniciar sesión(10 k/d)}/{1 + 0.4Iniciar sesión({R}_ _{mi}/{10}^{6}} = 1.2 + {0.18Iniciar sesión(10 (0.2)}/{1 + 0.4Iniciar sesión((2862000)/{10}^{6}}\)
\( {c}_ _{f0} = 1.246 \)
Esbeltez efectiva, \( λ \)
La esbeltez efectiva, \( λ \), para el poste se puede determinar a partir de la Tabla No.4 7.16 o y 1991-1-4.
\( λ = máx.(0.7 {z}_ _{gramo}/d, 70) \) para \( {z}_ _{gramo} \) > 50m
\( λ = máx.({z}_ _{gramo}/d, 70) \) para \( {z}_ _{gramo} \) < 15m
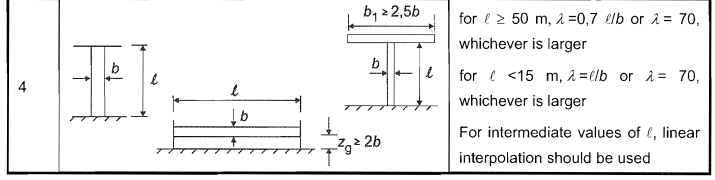
Figura 9. Mesa 7.16 o y 1991-1-4 para el cálculo de la esbeltez efectiva \( λ \).
Ya que \( {z}_ _{gramo} \) es igual a 38.0m, necesitamos interpolar los valores de \( λ \) para 50m y 15m:
\( {z}_ _{gramo} = 38\)
\( {λ}_ _{50m} = máx.(0.7 (38), 70) = 70 \)
\( {λ}_ _{15m} = máx.((38), 70) = 70 \)
Por lo tanto:
\( λ = 70 \)
Factor de efecto final, \( {ψ}_ _{λ} \)
El factor de efecto final, \( {ψ}_ _{λ} \), se puede obtener usando la Figura 7.36 o y 1991-1-4 requiriendo la relación de solidez \( Fi \) y esbeltez efectiva \( λ \). Supondremos relación de solidez \( Fi \) igual a 1.0 ya que la columna de tubería no tiene ninguna perforación.
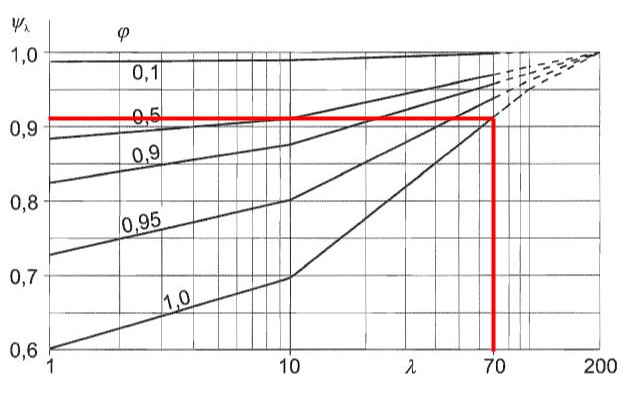
Figura 10. El factor de efecto final correspondiente \( {ψ}_ _{λ} \) para el poste que sostiene el letrero basado en la Figura 7.36 o y 1991-1-4.
De la figura 10, podemos deducir que el factor de efecto final \( {ψ}_ _{λ} \) porque el polo es igual a 0.910.
A partir de los parámetros calculados arriba,ya podemos calcular el Fuerza del viento, \( {F}_ _{w,Nuestro generador de carga se puede utilizar en cinco} \):
\({c}_ _{F} = {c}_ _{F,0}{ψ}_ _{λ} = (1.246)(0.910) = 1.134\)
\({F}_ _{w,Nuestro generador de carga se puede utilizar en cinco} = {c}_ _{s}{c}_ _{d}{c}_ _{F}{q}_ _{Precios}({z}_ _{mi}){A}_ _{árbitro,Nuestro generador de carga se puede utilizar en cinco} = (1.0)(1.134)(1129.89)(38.0×1.0) \)
\({F}_ _{w,Nuestro generador de carga se puede utilizar en cinco} = 48689.22 norte \)
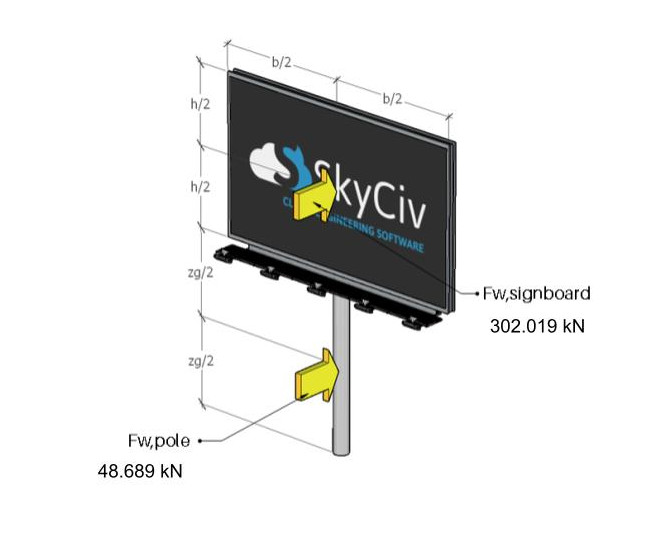
Figura 11. Las fuerzas del viento que actúan sobre el letrero y el poste.
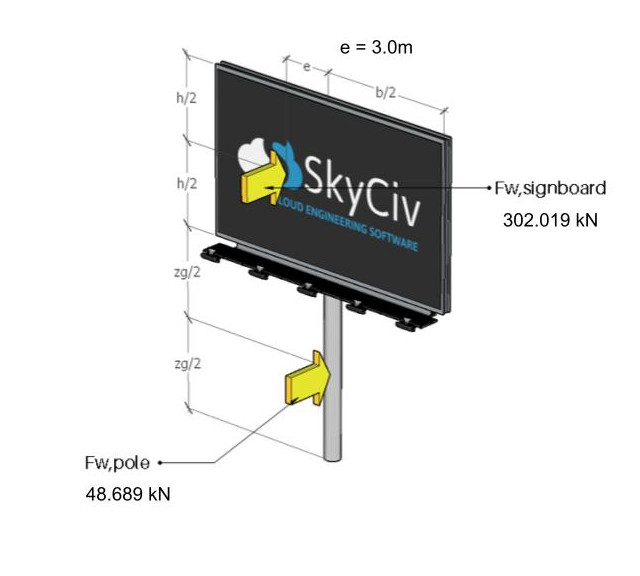
Figura 12. Las fuerzas del viento que actúan sobre el letrero y el poste para el caso excéntrico.
Generador de carga SkyCiv
Uso del generador de carga SkyCiv, puede obtener cargas de viento para letreros y postes con solo unos pocos clics y entradas. Cuando compra la versión independiente o se registra para una cuenta Profesional, podrá generar el informe de viento detallado para su proyecto de letrero!
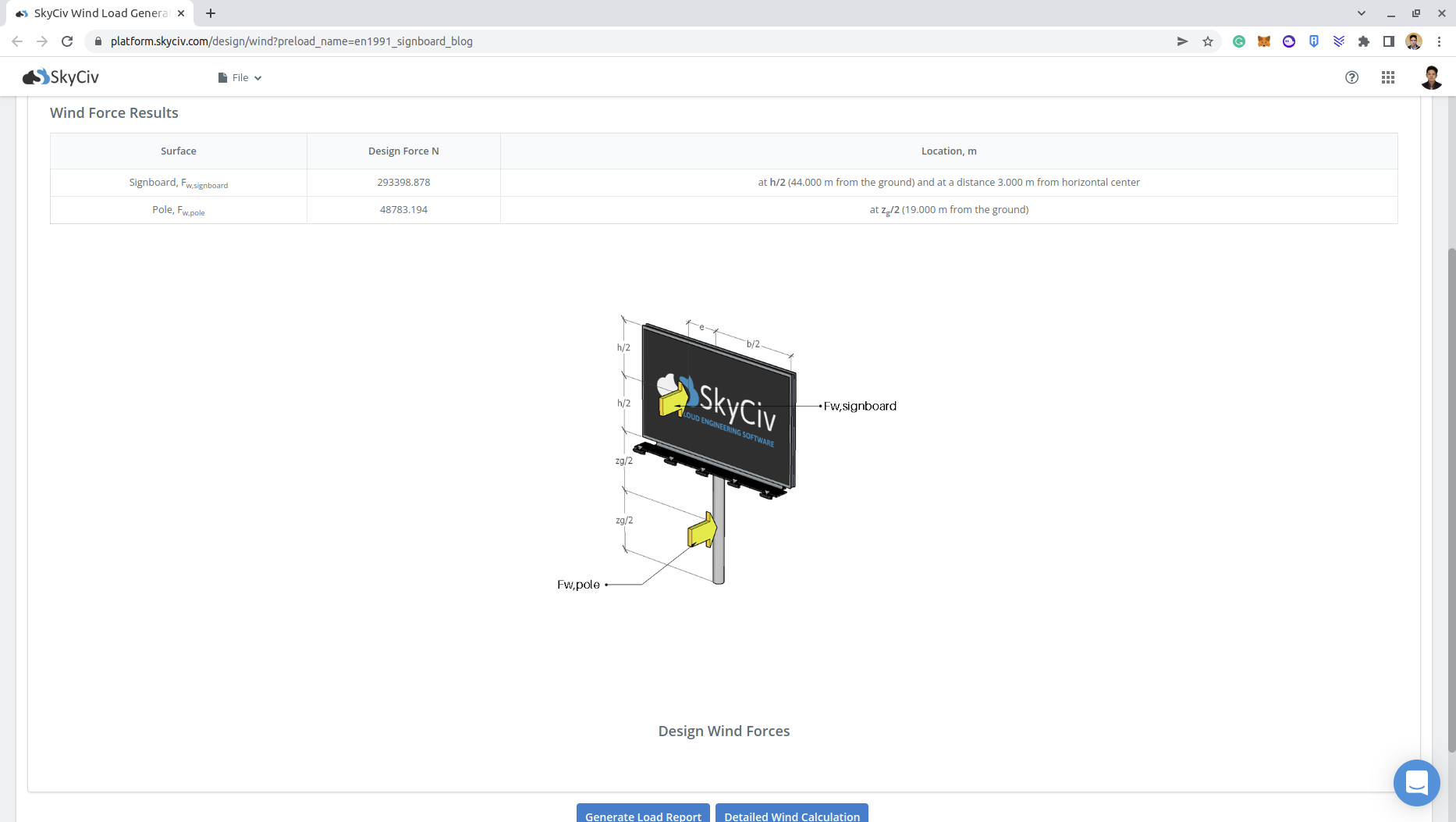
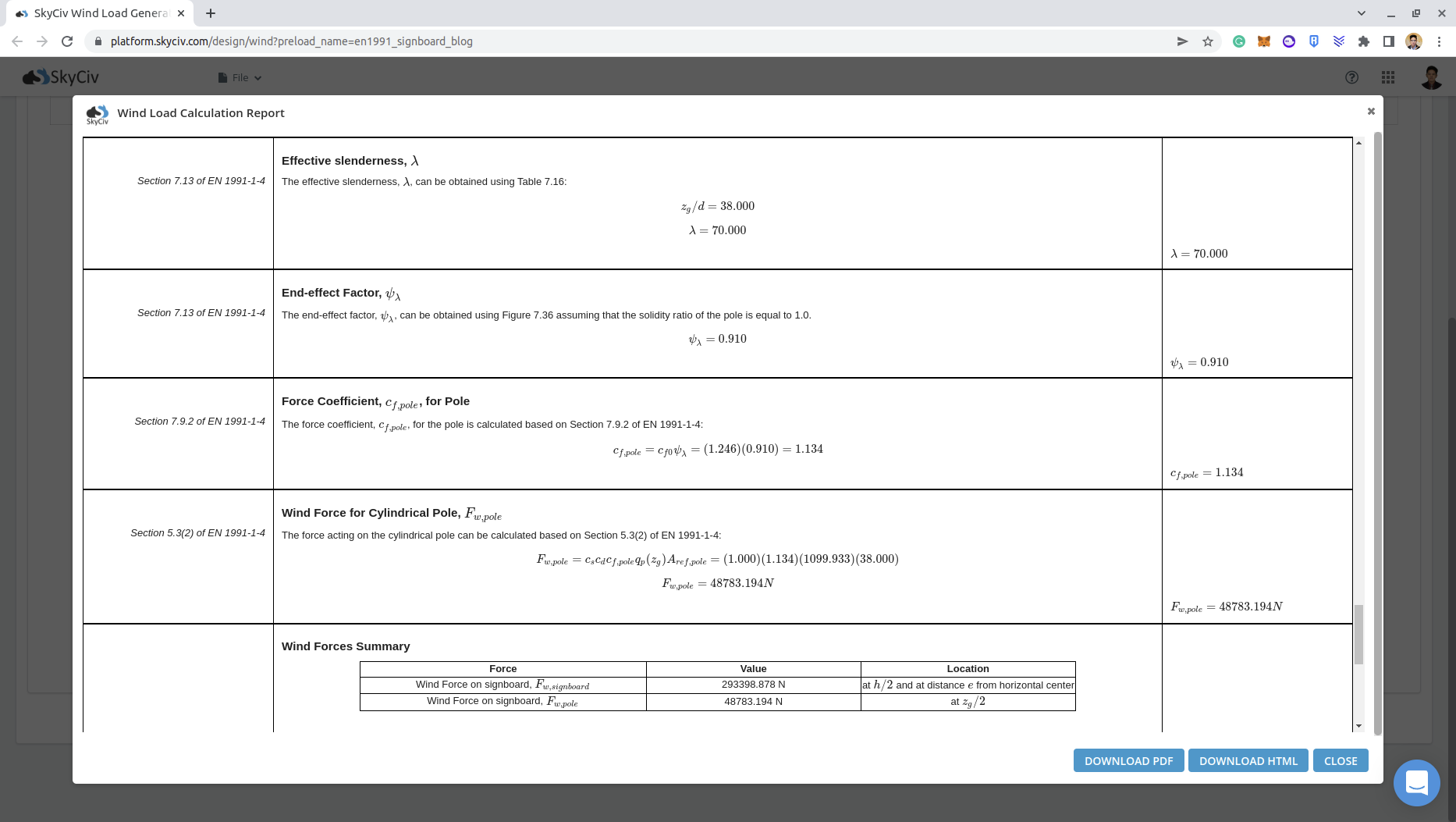
Puede consultar el informe detallado de carga de viento para el letrero a través de estos enlaces:
Ingeniero estructural, Desarrollo de Producto
Maestría en Ingeniería Civil
Referencias:
- En, B. (2005). Eurocódigo 1: Acciones sobre estructuras — Parte 1–4: Acciones generales: acciones de viento.
- BSI. (2005). BS ES 1991-1-4: 2005+ A1: 2010: Eurocódigo 1. Acciones sobre estructuras. Acciones generales. Acciones de viento.


