A continuación se muestra un ejemplo de algunos cálculos de placa base del código filipino que se usan comúnmente en el diseño de placa base. A menudo, al diseñar placas base, consideraremos algunos controles diferentes relacionados con los diversos componentes de una placa base, a saber:
- La base de hormigón – generalmente verificado contra las fuerzas de compresión y de apoyo en referencia a NSCP 2015
- las soldaduras – hay que revisar las soldaduras, para asegurarse de que proporcionen la sujeción adecuada y no fallen bajo estrés al NSCP 2015
- Pernos de anclaje – puede fallar debido a una serie de razones, como se muestra a continuación en los cálculos de diseño de pernos de anclaje de ejemplo para NSCP 2015
- miembro de acero (Columna) cheques – generalmente basado en estándares locales de diseño de acero
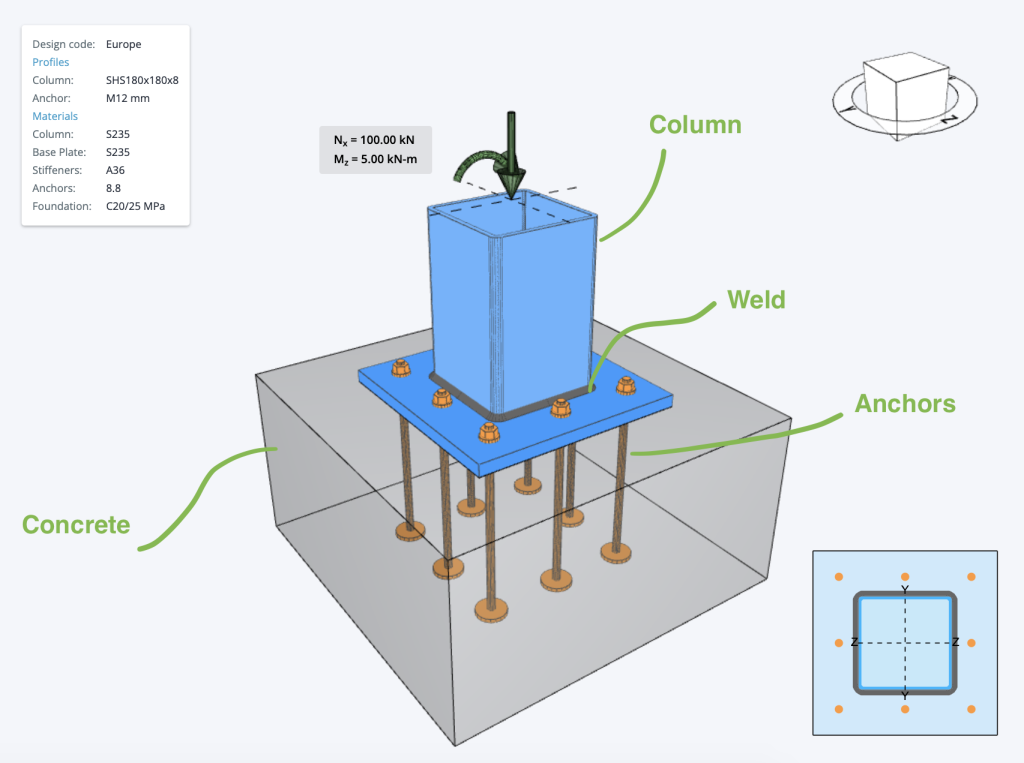
Actualmente, la Diseño de placa base de acero módulo implementa las siguientes comprobaciones a continuación. La versión de pago de este software., incluye cálculos detallados paso a paso, para que los ingenieros puedan revisar exactamente cómo se hacen estos cálculos!
Pruebe este cálculo usando SkyCiv Free Base Plate Calculator:
Combinaciones de carga:
El Diseño de placa base de acero los usos de combinaciones de carga factorizadas bajo NSCP 2015 se aplica de la siguiente manera:
- \(1.4D)
- \(1.2re + 1.6L + 0.5(L_{r} \texto{ o } R)\)
- \(1.2re + 1.6(Lr text{ o } R) + (f1L texto{ o } 0.5W)\)
- \(1.2re + 1.0W + f1L + 0.5(Lr \ \texto{ o } R)\)
- \(1.2re + 1.0E + f1L)
- \(0.9re + 1.0W )
- \(0.9re + 1.0MI)
dónde :
\(D) = carga muerta
\(L ) = carga viva
\(L_{r}\) = carga viva del techo
\(R ) = Carga de lluvia
\(MI) = Terremoto
\(W ) = Carga de viento
\(F_{1}\) = factor de carga viva (Valor por defecto = 1, Ver NSCP 2015 Sección de 203.3.1)
Pruebe este cálculo usando SkyCiv Free Base Plate Calculator:
NSCP 2015 Comprobación de cojinetes de hormigón:
El Diseño de placa base de acero comprueba la resistencia portante del hormigón (compresión) diseño según NSCP 2015 Eq. 510.8-2.
\( F_{b} = phi _{Llevando} \veces 0.85 \veces f'_{c} \veces sqrt{ \frac{ UNA_{2} }{ UNA_{1} } } \leq F_{b, límite} = 1.70 \veces f_{c} \veces A_{1} \)
dónde:
\( F'_{c} \) – resistencia a la compresión del hormigón
\( UNA_{1} \) - área de la placa base en contacto con la superficie del hormigón
\( UNA_{2} \) - superficie de apoyo de hormigón
\( \fi_{Llevando} \) – factor de resistencia para el hormigón ( valor predeterminado = 0.65 )
Pruebe este cálculo usando SkyCiv Free Base Plate Calculator:
NSCP 2015 Comprobación del diseño de soldadura:
El Diseño de placa base de acero comprueba la conformidad del diseño de soldadura con NSCP 2015 Ecuación 510.2-3
\( (i) R_{norte} = R_{nulo} + R_{nwt} \)
o
\( (ii) R_{norte} = 0.85R_{nulo} + 1.5R_{nwt} \)
dónde:
\(R_{nulo} \) = resistencia nominal total de las soldaduras de filete cargadas longitudinalmente.
\(R_{nwt} \) = resistencia nominal total de las soldaduras de filete cargadas transversalmente.
Pruebe este cálculo usando SkyCiv Free Base Plate Calculator:
NSCP 2015 Comprobación del diseño del anclaje:
El Diseño de placa base de acero comprueba los parámetros de anclaje se aplica utilizando las disposiciones del código de NSCP 2015 Sección de 417 | Anclaje a hormigón.
Se evalúan las siguientes resistencias de los pernos de anclaje:
- Resistencia del acero del ancla en tensión y cortante, \( \phi N_{a} \) y \( \no V_{a} \).
- Resistencia al desprendimiento del hormigón en tensión y cizallamiento, \( \phi N_{cbg} \) y \( \no V_{cbg} \).
- Resistencia a la extracción del hormigón, \( \phi N_{Precios} \).
- Fuerza de extracción del hormigón del anclaje a cortante, \( \no V_{cp} \).
Resistencia del acero del ancla en tensión y cortante
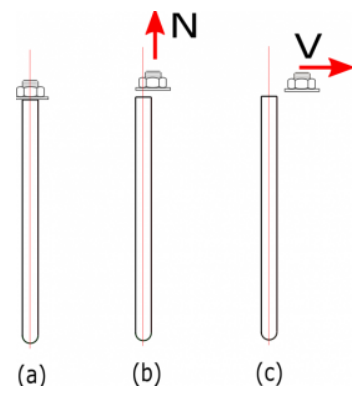
La resistencia factorizada del acero del anclaje en tracción y cortante se determina de acuerdo con NSCP 2015 Sección de 417.4.1 como
Para la tensión
\( \phi _{tensión, Congreso Nacional Africano} NORTE_{a} = phi _{tensión, Congreso Nacional Africano} UNA_{se,norte}F_{uta} \flecha correcta \) ecuación 17.6.1.2
Para cizalla
\( \phi _{el cortante, Congreso Nacional Africano} V_{a} = phi _{el cortante, Congreso Nacional Africano} 0.6UNA_{se,V }F_{uta} \flecha correcta \) ecuación 17.7.1.2b
dónde:
- \( \phi _{tensión, Congreso Nacional Africano} \) - factor de reducción de resistencia para anclajes en tensión ( valor predeterminado = 0.75 )
- \( \phi _{el cortante, Congreso Nacional Africano}\) - factor de reducción de resistencia para anclajes a cortante ( valor predeterminado = 0.65 )
- \( UNA_{se,norte}\) - es el área de la sección transversal efectiva de un ancla en tensión.
- \( UNA_{se,V }\) - es el área de la sección transversal efectiva de un ancla en cortante.
- \( F_{uta}\) – la resistencia a la tracción especificada del acero del anclaje y no debe ser mayor que \(1.9F_{sí}\) y 125 KSI (861.845 Mpa)
Resistencia a la rotura del hormigón
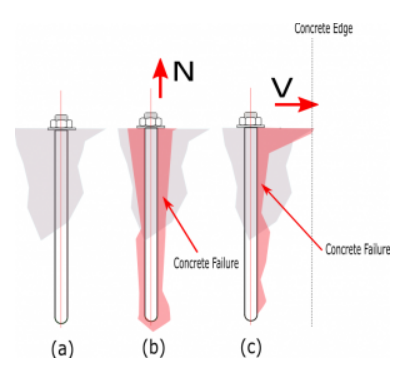
La resistencia al desprendimiento del hormigón factorizado del anclaje en tracción y cortante se determina de acuerdo con NSCP 2015 Ecuación 417.4.2.1b y NSCP 2015 Ecuación 417.5.2.1b como
\( \phi N_{cbg} = phi frac{ UNA_{Carolina del Norte} }{ UNA_{Recuerda} } \psi_{CE,norte} \psi_{ed,norte} \psi_{c,norte} \psi_{cp,norte} NORTE_{b} \flecha correcta \) 417.4.2.1b
dónde:
\( \fi \) – factor de reducción de resistencia para anclajes en tensión ( valor predeterminado = 0.75 ).
\( UNA_{Carolina del Norte} \) – Falla proyectada de hormigón de anclajes individuales o grupales..
\( UNA_{Recuerda} \)- Proyecto de área de falla de concreto de un solo anclaje, para el cálculo de la resistencia en tensión si no está limitado por la distancia al borde o el espaciado.
\( \psi_{CE,norte} \) – Factor utilizado para modificar la resistencia a la tracción de los anclajes según la excentricidad de las cargas aplicadas.
\( \psi _{CE,norte} = frac{1.00}{ 1 + \frac{2 \veces e^{"}_ _{norte}}{3 \veces h_{ef}} } \leq 1.00 \flecha correcta \) Ecuación 417.4.5.3
\( \psi_{ed,norte} \) – Factor utilizado para modificar la resistencia a la tracción del anclaje.
(a) \( \texto{Si } C_{a,min} \geq 1.5h_{ef} \texto{ luego } \psi _{ed,norte} = 1.00 \)
y
(b) \( \texto{Si } C_{a,min} < 1.5h_{ef} \texto{ luego } \psi _{ed,norte} = 0.70 + 0.3\frac{C_{a,min}}{1.5h_{ef}} \) Ecuación 417.4.2.5b
\( \psi_{c,norte} \) - Factor de ruptura de grietas en tensión.
\( \psi _{c,norte} = 1.25 \) para anclajes empotrados
\( \psi_{cp,norte} \) - Factor de ruptura en tensión.
(a) \( \texto{Si } C_{a,min} \geq C_{C.A} \texto{ luego } \psi _{cp,norte} = 1.00 \) ecuación 17.6.2.4.1a
y
(b) \( \texto{Si } C_{a,min} < C_{C.A} \texto{ luego } \psi _{cp,norte} = frac{ C_{a,min} }{ C_{C.A}} \geq frac{ 1.5h_{ef} }{ C_{C.A} } \) ecuación 17.6.2.4.1b
\( NORTE_{b} \) – resistencia básica al desprendimiento del hormigón en tensión de un solo anclaje en hormigón fisurado.
Resistencia a la extracción del hormigón
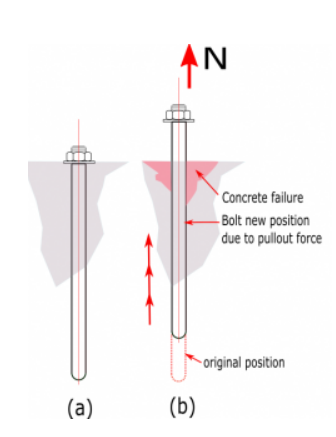
La resistencia a la extracción del hormigón factorizado de un anclaje se define en NSCP 2015 Ecuación 417.4.3.4 como
ϕNpn = ϕΨc,PAG nortePrecios
dónde:
\( \fi \) – factor de reducción de resistencia para anclajes en tensión ( valor predeterminado = 0.70 ).
\( \psi _{c, PAG} \) – factor de modificación para la condición del hormigón
Para hormigón fisurado:
\( \psi _{c, PAG} \) = 1.0
Para hormigón no fisurado:
\( \psi _{c, PAG} \) = 1.4
\( NORTE_{Precios} \) – Fuerza de extracción del ancla
Para hormigón fisurado:
\( NORTE_{Precios} = 8A_{brg}f ^{"}_ _{c}\flecha correcta \) Ecuación 417.4.3.4
Para hormigón no fisurado:
\( NORTE_{Precios} = 0.9f ^{"}_ _{c}mi_{h}D_{a} \flecha correcta \) Ecuación 417.4.3.5
dónde \( 3D_{a} \leq e_{h} \leq 4.5d_{a} \)
\( f ^{"}_ _{c} \) – resistencia a la compresión especificada del hormigón.
\( UNA_{brg} \) – área de apoyo neta de la cabeza del montante, perno de anclaje o barra deformada con cabeza.
\( mi_{h} \) – distancia desde la superficie interior del eje de un perno en J o un perno en L a la punta exterior de la J- o perno en L.
\( D_{a} \) – diámetro exterior del ancla o diámetro del eje del perno con cabeza, perno con cabeza, o perno en forma de gancho.

