Guía de cálculo en el diseño de una zapata aislada basada en CSA A23.3-14

SkyCiv Foundation cubre el diseño de cimientos aislados conforme a CSA A23.3-14¹ y NBCC 2010².

¿Quieres probar el software de diseño de la fundación SkyCiv?? Nuestra herramienta permite a los usuarios realizar cálculos de diseño de la base sin ninguna descarga o instalación!

Calculadora de diseño de cimientos

Parámetros de diseño de una zapata aislada

Algunos cálculos presentados son similares con ACI 318, que es también una de las referencias de su homólogo CSA.

Requisitos de dimensión

Para determinar las dimensiones de una zapata aislada, servicio o cargas no factorizadas, como muerto (re), En Vivo (L), Viento (W), Sísmico (E), etc. se aplicará utilizando combinaciones de carga, según lo definido por NBCC 2010. Cualquier combinación de carga que gobierne se considerará la carga de diseño, y se dividirá a la presión del suelo permisible como se muestra en la Ecuación 1.

\(\texto{A} = frac{\texto{PAGS}_ _{\texto{norte}}}{\texto{q}_ _{\texto{todos}}} \flecha correcta \) Ecuación 1

dónde:
q_todos = presión de suelo permitida
PAGS_norte = carga de diseño no factorizada
A = área de cimentación

Cizalla unidireccional

para verificar cizalla unidireccional, el plano de corte crítico (Consulte la figura 1) se encuentra a distancia “re” de la cara de una columna.

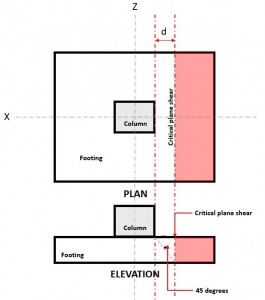
Figura 1. Corte crítico en plano de corte unidireccional

El De una sola mano corte Demanda o V _F se calcula asumiendo que la base está en voladizo lejos de la columna donde está el área (rojo) indicado en la Figura 2, de acuerdo con CSA A23.3-14, Sección de 13.3.6.

El Capacidad de corte unidireccional o V _c se define como la resistencia al corte máxima y se calcula utilizando la ecuación 2 por CSA A23.3-14, Sección de 11.3.4.

\(\texto{V }_ _{\texto{c}} = phi _{\texto{c}} \veces lambda veces sqrt{\texto{F'}_ _{\texto{c}}} \tiempos texto{b}_ _{\texto{w}} \tiempos texto{re} \flecha correcta \) Ecuación 2 (CSA A23.3-14 Equivalente. 11-6)

dónde:
ϕ_c = factor de resistencia del hormigón
λ = factor de modificación para la densidad del hormigón
F’_c = resistencia especificada del concreto, MPa
b_w = ancho de la zapata, mm
d = profundidad de corte efectiva, mm

La demanda de corte y la capacidad de corte deben cumplir con la siguiente ecuación para cumplir con los requisitos de diseño de CSA A23.3-14:

\(\texto{V }_ _{\texto{F}} \leq phi text{V }_ _{\texto{c}} \flecha correcta \) Ecuación 3 (CSA A23.3-14 Eq. 11.3)

Fundación SkyCiv, en cumplimiento de la ecuación 3, calcula la relación de unidad de corte unidireccional (Ecuación 4) tomando demanda de corte sobre la capacidad de corte.

\( \texto{Ratio de unidad} = frac{\texto{Demanda de corte}}{\texto{Capacidad de corte}} \flecha correcta \) Ecuación 4

Cizalla bidireccional

El Cizalla bidireccional estado límite, también conocido como cizalla de perforación, extiende su sección crítica a una distancia “d / 2” desde la cara de la columna y alrededor del perímetro de la columna. El plano crítico de corte se encuentra en esa sección de la zapata (Consulte la figura 2).

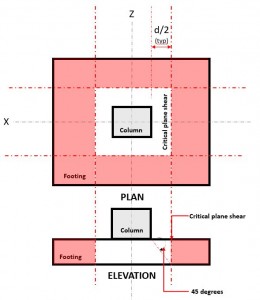
Figura 2. Plano crítico de corte de corte bidireccional

El Dos caminosescuchar demanda o V _F ocurre en el plano crítico de corte, ubicado a una distancia de “d / 2” donde el (rojo) área sombreada, indicado en la Figura 2, de acuerdo con CSA A23.3-14, Sección de 13.3.3.

El Capacidad de corte o V _c se rige por el valor mínimo calculado mediante la Ecuación 5, 6, y 7 por CSA A23.3-14, Sección de 13.3.4.1

\(\texto{V }_ _{\texto{c}} = left ( 1 + \frac{2}{\beta_{\texto{c}}} \verdad ) \veces 0.19 \tiempos lambda tiempos phi _{\texto{c}} \veces sqrt{F'_{c}} \flecha correcta \) Ecuación 5 (CSA A23.3-14 Eq. 13.5)

\(\texto{V }_ _{\texto{c}} = left ( \frac{\alfa_{\texto{s}} \tiempos texto{re}}{\texto{b}_ _{\texto{los}}} + 0.19 \verdad ) \tiempos lambda tiempos phi _{\texto{c}} \veces sqrt{F'_{c}} \flecha correcta \) Ecuación 6 (CSA A23.3-14 Eq. 13.6)

\(\texto{V }_ _{\texto{c}} = 0.38 \tiempos lambda tiempos phi _{\texto{c}} \veces sqrt{F'_{c}} \flecha correcta \) Ecuación 7 (CSA A23.3-14 Eq. 13.7)

Nota: si_c es la relación entre el lado largo y el lado corto de la columna, carga concentrada, o área de reacción y α_s es dado por 13.3.4.1

dónde:
λ = factor de modificación para la densidad del hormigón
F’_c = resistencia específica del hormigón a la compresión, MPa
d = distancia de la fibra de compresión extrema al centroide del refuerzo de tensión longitudinal, mm

La demanda de corte y la capacidad de corte deben cumplir con la siguiente ecuación para cumplir con los requisitos de diseño de CSA A23.3-14:

\(\texto{V }_ _{\texto{F}} \leq phi text{V }_ _{\texto{c}} \flecha correcta \) Ecuación 8 (CSA A23.3-14 Eq. 11.3)

Fundación SkyCiv, en cumplimiento de la ecuación 8, calcula la relación de unidad de corte bidireccional (Ecuación 9) tomando demanda de corte sobre la capacidad de corte.

\( \texto{Ratio de unidad} = frac{\texto{Demanda de corte}}{\texto{Capacidad de corte}} \flecha correcta \) Ecuación 9

Pruebas de diseño de flexión

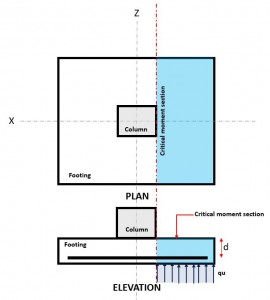
Figura 3. Sección de flexión crítica

El Flexural El estado límite se produce en la sección de flexión crítica, ubicado en la cara de la columna en la parte superior de la zapata (Consulte la figura 3).

El Demanda de momento, o M_F se encuentra en la sección de flexión crítica (área de escotilla azul) indicado en la Figura 3, y se calcula usando la ecuación 10.

\( \texto{M}_ _{tu} = text{q}_ _{tu} \veces left ( \frac{l_{x}}{2} – \frac{C_{x}}{2} \verdad ) \veces l_{z} \veces left ( \frac{\frac{l_{x}}{2} – \frac{C_{x}}{2} }{2} \verdad ) \flecha correcta \) Ecuación 10

dónde:
q_tu = presión factorizada del suelo, kPa
l_x = dimensión de pie a lo largo del eje x, mm
l_z = dimensión de pie a lo largo del eje z, mm
c_x = dimensión de la columna a lo largo del eje x, mm

El Resistencia de momento, o Mr se calcula usando la ecuación 11.

\( \texto{M}_ _{r} = phi_{\texto{s}} \veces A_{s} \veces f_{y} \veces left( re – \frac{a}{2} \verdad) \flecha correcta \) Ecuación 11

dónde:
ϕ_s = factor de resistencia para barras de refuerzo no pretensadas
d = distancia de la fibra de compresión extrema al centroide del refuerzo de tensión longitudinal, mm
A_s = área de refuerzo, mm²
a = profundidad del bloque de tensión rectangular equivalente, mm
fy = resistencia de refuerzo, MPa

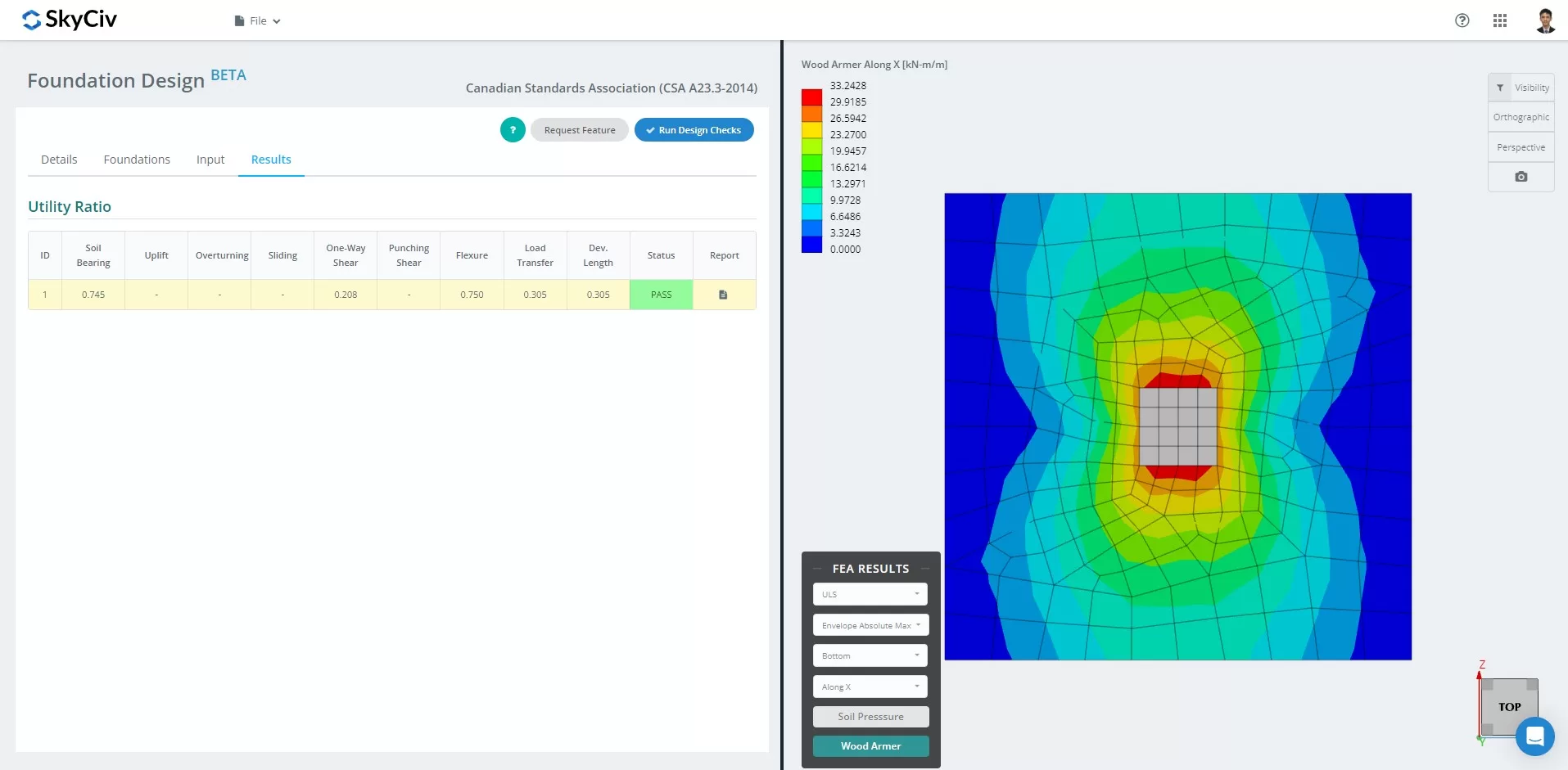
NUEVA Fundación SkyCiv con FEA

A partir de marzo 2024, el Módulo de Diseño de Cimentaciones ha integrado el Análisis de Elementos Finitos (FEA) solucionador en sus capacidades. This new feature allows users to conduct in-depth soil pressure and wood armer analyses while still performing all structural checks specified by CSA A23.3-14, incluyendo todas las verificaciones mencionadas anteriormente. El resumen de los resultados de la FEA se incluye en el informe completo..